H max формула как вывести

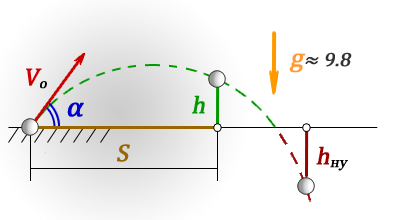
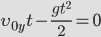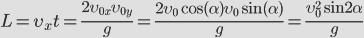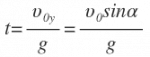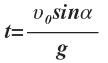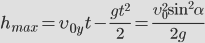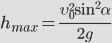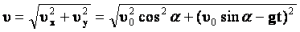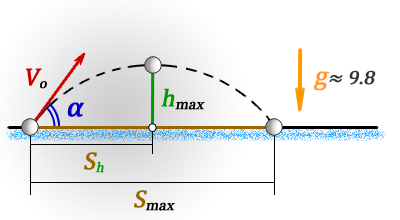
Формулы для максимальной высоты и дальности тела брошенного под углом к горизонту. Время подъема на макс. высоту.

h max — максимальная высота

S max — максимальная дальность полета, если бросок и падение на одном уровне

S h — расстояние пройденное по горизонтали до момента максимального подъема

t max — время всего полета

t h — время за которое тело поднялось на максимальную высоту

V o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с 2 — ускорение свободного падения

Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте S h и угол α под которым брошено тело . :

По этой формуле, можно определить максимальную высоту, если известно время t h за которое тело поднялось на эту высоту . :

или известны максимальная высота h max и угол α под которым брошено тело . :

или известны максимальная высота h max и угол α под которым брошено тело . :

* т. к. траектория движения симметрична относительно линии максимальной высоты, то расстояние S h ровно в два раза, меньше максимальной дальности броска S max

* т. к. траектория движения симметрична относительно линии максимальной высоты, то время максимального подъема t h ровно в два раза, меньше максимального времени t max

Формула для определения времени за которое тело поднялось на максимальную высоту, если даны, начальная скорость V o и угол α под которым брошено тело или если известна только максимальная высота h max :

Источник

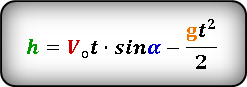
Найти высоту тела брошенного под углом к горизонту

h — высота тела в момент времени t

h ну — высота ниже уровня броска (принимает отрицательное значение)

S — дальность полета по горизонтали

t — время полета

V o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с 2 — ускорение свободного падения

h ну — высота ниже уровня броска, принимает отрицательное значение

h max — максимальная высота

S max — максимальная дальность полета, если бросок и падение на одном уровне

S h — расстояние пройденное по горизонтали до момента максимального подъема

t max — время всего полета

t h — время за которое тело поднялось на максимальную высоту

V o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с 2 — ускорение свободного падения

Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте S h и угол α под которым брошено тело . :

По этой формуле, можно определить максимальную высоту, если известно время t h за которое тело поднялось на эту высоту . :

Источник

Формулы кинематики с пояснениями по физике

Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.

Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.

Путь, время, скорость

Равномерное движение

• x — координата
• x₀ — начальная координата
• v — скорость
• t — время

Равномерно ускоренное движение: ускорение

• a — ускорение
• v — скорость
• v₀ — начальная скорость
• t — время

Равномерно ускоренное движение: скорость

• v — скорость
• v₀ — начальная скорость
• a — ускорение
• t — время

Равномерно ускоренное движение: путь

• s — путь
• v — скорость
• t — время
• a — ускорение

Равномерно ускоренное движение: координата

• x — координата
• x₀ — начальная координата
• v — скорость
• t — время
• a — ускорение

Высота тела, брошенного вертикально вверх (вниз)

h=h_0 + v_ < 0 >t — \frac < gt^2 >

• h — высота
• h₀ — начальная высота
• v₀ — начальная скорость
• t — время
• g — ускорение свободного падения

Скорость тела, брошенного вертикально вверх (вниз)

• v — скорость
• v₀ — начальная скорость
• g — ускорение свободного падения
• t — время

Скорость, ускорение, время

Скорость свободно падающего тела

• v — скорость
• g — ускорение свободного падения
• t — время

Центростремительное ускорение

• a — центростремительное ускорение
• v — скорость
• R — радиус

Угловая скорость

• ω — угловая скорость
• φ — угол
• t — время

Равномерное круговое движение

• l — длина дуги окружности
• R — радиус
• φ — угол

Равномерное круговое движение: линейная скорость

• v — линейная скорость
• R — радиус
• ω — угловая скорость

Период вращения

• T — период
• t — время
• N — число вращений

• T — период
• R — радиус
• v — линейная скорость

• T — период
• ω — угловая скорость

Центростремительное ускорение

• a — центростремительное ускорение
• R — радиус
• T — период вращения

• a — центростремительное ускорение
• R — радиус
• n — частота вращения

Частота вращения

• n — частота вращения
• T — период вращения

Центростремительное ускорение

• a — центростремительное ускорение
• ω — угловая скорость
• R — радиус

Дальность броска тела, брошенного под углом к горизонту

• x — координата (дальность)
• v₀ — начальная скорость
• t — время
• α — угол

Высота подъема тела, брошенного под углом к горизонту

y=v_0t \sin (\alpha) — \frac < gt^2 >

• y — координата (высота подъема )
• v₀ — начальная скорость
• t — время
• g — ускорение свободного падения
• α — угол

Вертикальная скорость тела, брошенного под углом к горизонту

v_y=v_0* \sin (\alpha) — gt

• v_y — вертикальная скорость
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения
• t — время

Максимальная высота подъема тела, брошенного под углом к горизонту

• h_макс — максимальная высота
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения

Общее время движения тела, брошенного под углом к горизонту

• t — время
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения

Дальность броска тела, брошенного горизонтально

• x — координата (дальность)
• x₀ — начальная координата
• v — скорость
• t — время

Высота подъема тела, брошенного горизонтально

• y — координата (высота подъема)
• y₀ — начальная координата (высота)
• g — ускорение свободного падения
• t — время

Общее время движения тела, брошенного горизонтально

• t_макс — максимальное время
• h — высота
• g — ускорение свободного падения

Источник

Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно:

Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Источник

Движение тела, брошенного горизонтально или под углом к горизонту.
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты. Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
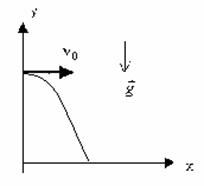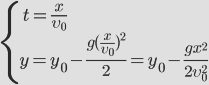	— между координатами квадратичная зависимость, траектория – парабола!
Следовательно, для решения этой задачи необходимо решить уравнение
Оно будет иметь решение при t=0 (начало движения) и
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.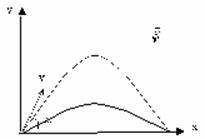
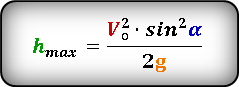
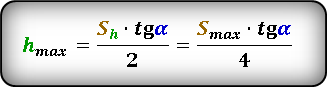
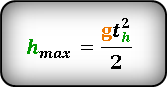
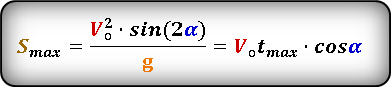
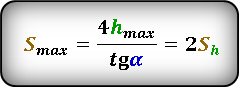
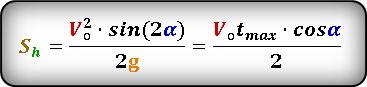
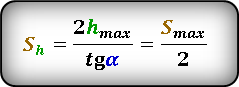
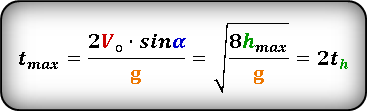
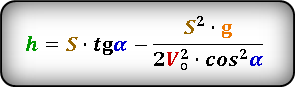
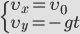
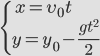
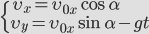
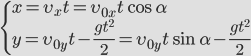
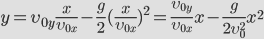