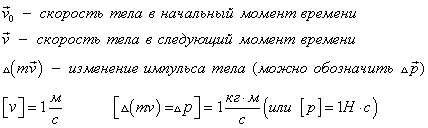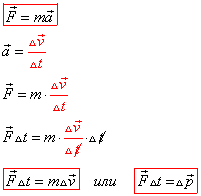Как найти изменение импульса тела выведите формулу

I. Механика

Тестирование онлайн

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

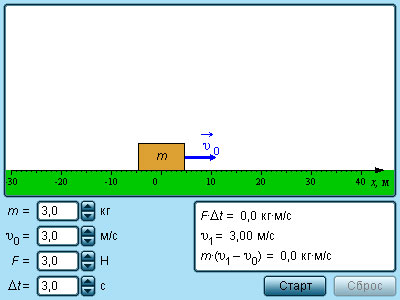
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

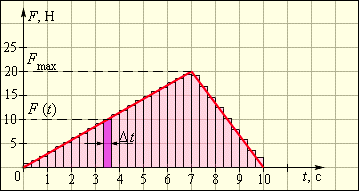
График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Источник

Как найти изменение импульса тела выведите формулу

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Средняя равнодействующая сила

ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Тестирование онлайн

Замкнутая система тел

Это система тел, которые взаимодействуют только друг с другом. Нет внешних сил взаимодействия.

В реальном мире такой системы не может быть, нет возможности убрать всякое внешнее взаимодействие. Замкнутая система тел — это физическая модель, как и материальная точка является моделью. Это модель системы тел, которые якобы взаимодействуют только друг с другом, внешние силы не берутся во внимание, ими пренебрегают.

Закон сохранения импульса

В замкнутой системе тел векторная сумма импульсов тел не изменяется при взаимодействии тел. Если импульс одного тела увеличился, то это означает, что у какого-то другого тела (или нескольких тел) в этот момент импульс уменьшился ровно на такую же величину.

Рассмотрим такой пример. Девочка и мальчик катаются на коньках. Замкнутая система тел — девочка и мальчик (трением и другими внешними силами пренебрегаем). Девочка стоит на месте, ее импульс равен нулю, так как скорость нулевая (см. формулу импульса тела). После того как мальчик, движущийся с некоторой скоростью, столкнется с девочкой, она тоже начнет двигаться. Теперь ее тело обладает импульсом. Численное значение импульса девочки ровно такое же, на сколько уменьшился после столкновения импульс мальчика.

Одно тело массой 20кг движется со скоростью , второе тело массой 4кг движется в том же направлении со скоростью . Чему равны импульсы каждого тела. Чему равен импульс системы?

Импульс системы тел — это векторная сумма импульсов всех тел, входящих в систему. В нашем примере, это сумма двух векторов (так как рассматриваются два тела), которые направлены в одну сторону, поэтому

Сейчас вычислим импульс системы тел из предыдущего примера, если второе тело двигается в обратном направлении.

Так как тела двигаются в противоположных направлениях, получаем векторную сумму импульсов разнонаправленных. Подробнее о сумме векторов.

Главное запомнить

1) Что такое замкнутая система тел;
2) Закон сохранения импульса и его применение

Источник

Импульс тела

Если на тело массой m за определенный промежуток времени Δ t действует сила F → , тогда следует изменение скорости тела ∆ v → = v 2 → — v 1 → . Получаем, что за время Δ t тело продолжает движение с ускорением:

a → = ∆ v → ∆ t = v 2 → — v 1 → ∆ t .

Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:

F → = m a → = m v 2 → — v 1 → ∆ t или F → ∆ t = m v 2 → — m v 1 → = m ∆ v → = ∆ m v → .

Изменение импульса

Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.

Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду ( к г м / с ) .

Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.

Импульс относят к векторным величинам. Существует еще одна формулировка определения.

Изменение импульса тела равняется импульсу силы.

При обозначении импульса p → второй закон Ньютона записывается как:

Данный вид позволяет формулировать второй закон Ньютона. Сила F → является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:

F x Δ t = Δ p x ; F y Δ t = Δ p y ; F z Δ t = Δ p z .

Рисунок 1 . 16 . 1 . Модель импульса тела.

Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.

Одномерное движение – это движение тела по одной из координатный осей.

На примере рассмотрим свободное падение тела с начальной скоростью v 0 под действием силы тяжести за промежуток времени t . При направлении оси O Y вертикально вниз импульс силы тяжести F т = mg , действующий за время t , равняется m g t . Такой импульс равняется изменению импульса тела:

F т t = m g t = Δ p = m ( v – v 0 ) , откуда v = v 0 + g t .

Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t . Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы F с р из временного промежутка t . Рисунок 1 . 16 . 2 показывает, каким образом определяется импульс силы, которая зависит от времени.

Рисунок 1 . 16 . 2 . Вычисление импульса силы по графику зависимости F ( t )

Необходимо выбрать на временной оси интервал Δ t , видно, что сила F ( t ) практически неизменна. Импульс силы F ( t ) Δ t за промежуток времени Δ t будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δ t i на промежутке от от 0 до t , сложить импульсы всех действующих сил из этих промежутков Δ t i _, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.

Применив предел ( Δ t i → 0 ) , можно найти площадь, которая будет ограничиваться графиком F ( t ) и осью t . Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F ( t ) из интервала [ 0 ; t ] .

Рисунок 1 . 16 . 2 показывает импульс силы, находящийся на интервале от t 1 = 0 с до t 2 = 10 .

Из формулы получим, что F с р ( t 2 — t 1 ) = 1 2 F m a x ( t 2 — t 1 ) = 100 Н · с = 100 к г · м / с .

То есть, из примера видно F с р = 1 2 F m a x = 10 Н .

Определение средней силы

Имеются случаи, когда определение средней силы F с р возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0 , 415 к г можно сообщить скорость, равную v = 30 м / с . Приблизительным временем удара является значение 8 · 10 – 3 с .

Тогда формула импульса приобретает вид:

p = m v = 12 , 5 к г · м / с .

Чтобы определить среднюю силу F с р во время удара, необходимо F с р = p ∆ t = 1 , 56 · 10 3 Н .

Получили очень большое значение, которое равняется телу массой 160 к г .

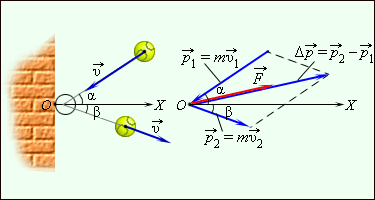
Когда движение происходит по криволинейной траектории, то начальное значение p 1 → и конечное
p 2 → могут быть различны по модулю и по направлению. Для определения импульса ∆ p → применяют диаграмму импульсов, где имеются векторы p 1 → и p 2 → , а ∆ p → = p 2 → — p 1 → построен по правилу параллелограмма.

Для примера приводится рисунок 1 . 16 . 2 , где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v 1 → налетает на поверхность под углом α к нормали и отскакивает со скоростью v 2 → с углом β . При ударе в стену мяч подвергался действию силы F → , направленной также, как и вектор ∆ p → .

Рисунок 1 . 16 . 3 . Отскакивание мяча от шероховатой стенки и диаграмма импульсов.

Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v 1 → = v → , тогда при отскоке она изменится на v 2 → = — v → . Значит, за определенный промежуток времени импульс изменится и будет равен ∆ p → = — 2 m v → . Используя проекции на О Х , результат запишется как Δ p x = – 2 m v x . Из рисунка 1 . 16 . 3 видно, что ось О Х направлена от стенки, тогда следует v x 0 и Δ p x > 0 . Из формулы получим, что модуль Δ p связан с модулем скорости, который принимает вид Δ p = 2 m v .

Источник