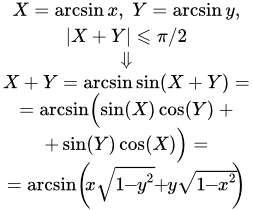Как вывести аргумент синуса

Вывод формул обратных тригонометрических функций

Основные формулы

Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.

В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin x ) = x
cos(arccos x ) = x
tg(arctg x ) = x ( –∞ )
ctg(arcctg x ) = x ( –∞ )

Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin x ) = x при
arccos(cos x ) = x при
arctg(tg x ) = x при
arcctg(ctg x ) = x при

Если переменная x не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n — целое):
sin x = sin(– x–π ) ; sin x = sin( π–x ) ; sin x = sin( x+ 2 πn ) ;
cos x = cos( –x ) ; cos x = cos( 2 π–x ) ; cos x = cos( x+ 2 πn ) ;
tg x = tg( x+πn ) ; ctg x = ctg( x+πn )

Например, если известно, что то
arcsin(sin x ) = arcsin(sin( π — x )) = π — x .

Легко убедиться, что при π – x попадает в нужный интервал. Для этого умножим на –1 : и прибавим π : или Все правильно.

Обратные функции отрицательного аргумента

Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.

arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x

Поскольку то умножив на –1 , имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.

Аналогично для остальных функций.
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x

arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x

arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x

Выражение арксинуса через арккосинус и арктангенса через арккотангенс

Выразим арксинус через арккосинус.

Формула справедлива при Эти неравенства выполняются, поскольку

Чтобы убедиться в этом, умножим неравенства на –1 : и прибавим π/2 : или Все правильно.

Аналогично выражаем арктангенс через арккотангенс.

Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот

Поступаем аналогичным способом.

Формулы суммы и разности

Аналогичным способом, получим формулу суммы арксинусов.

Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin x , Y = arcsin y . Формула применима при
. Далее замечаем, что, поскольку arcsin(– x ) = – arcsin x, arcsin(– y ) = – arcsin y, то при разных знаках у x и y , X и Y также разного знака и поэтому неравенства выполняются. Условие различных знаков у x и y можно написать одним неравенством: . То есть при формула справедлива.

Теперь рассмотрим случай x > 0 и y > 0 , или X > 0 и Y > 0 . Тогда условие применимости формулы заключается в выполнении неравенства: . Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0 , до π , то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ; то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin X = sin arcsin x = x :
;
;
;
.

Итак, полученная формула справедлива при или .

Теперь рассмотрим случай x > 0, y > 0 и x 2 + y 2 > 1 . Здесь аргумент синуса принимает значения: . Его нужно привести к интервалу области значения арксинуса :

Итак,

при 0,\,y>0 \;» style=»width:114px;height:18px;vertical-align:-10px;background-position:-358px -667px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> .

Заменив x и y на – x и – y , имеем

при 0,\, — y>0 \;» style=»width:144px;height:18px;vertical-align:-10px;background-position:-340px -649px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> .
Выполняем преобразования:

при и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> .
Или

при и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> .

Итак, мы получили следующие выражения для суммы арксинусов:

при или ;

при 0, \, y > 0 \;» style=»width:114px;height:18px;vertical-align:-10px;background-position:-472px -667px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-600px -510px»> ;

при и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-600px -510px»> .

Аналогичным способом получаются остальные формулы:

при или ;

при 0,\,y и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> ;

при 0 \;» style=»width:108px;height:18px;vertical-align:-10px;background-position:-808px -667px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-294px -510px»> ;

при ;

при 0,\;xy>1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-0px -667px»> ;

при 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-122px -667px»> ;

при -1″ style=»width:76px;height:18px;vertical-align:-10px;background-position:-85px -685px»> ;

при 0,\;xy ;

при .

Автор: Олег Одинцов . Опубликовано: 19-07-2014

Источник

Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом

Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg

Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.

Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.

Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса

Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.

д л я α ∈ — 1 , 1 sin ( a r c c i s α ) = α , cos ( a r c cos α ) = α , д л я α ∈ ( — ∞ , ∞ ) t g ( a r c t g α ) = α , c t g ( a r c c t g α ) = α

Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.

Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса

д л я — π 2 ≤ α ≤ π 2 a r c sin ( sin α ) = α , д л я 0 ≤ α ≤ π arccos ( cos α ) = α , д л я — π 2 α π 2 arctg ( tg α ) = α , д л я 0 α π arcctg ( ctg α ) = α

Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.

Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел

В этом блоке мы сформулируем важное утверждение:

Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.

д л я α ∈ — 1 , 1 a r c c i s ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , д л я α ∈ ( — ∞ , ∞ ) a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — arcctg α

Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.

Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс

Они выглядят следующим образом:

д л я α ∈ — 1 , 1 a r c c i s α + a r c cos α = π 2 , д л я α ∈ ( — ∞ , ∞ ) a r c t g α + a r c c t g α = π 2

Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.

Формулы связи между прямыми и обратными тригонометрическими функциями

Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.

— 1 ≤ α ≤ 1 , sin ( a r c sin α ) = α	— 1 ≤ α ≤ 1 , sin ( a r c cos α ) = 1 — α 2	— ∞ ≤ α ≤ + ∞ , sin ( a r c t g α ) = α 1 + α 2	— ∞ ≤ α ≤ + ∞ , sin ( a r c c t g α ) = 1 1 + α 2
— 1 ≤ α ≤ 1 , cos ( a r c sin α ) = 1 — α 2	— 1 ≤ α ≤ 1 , cos ( a r c cos α ) = α	— ∞ ≤ α ≤ + ∞ , cos ( a r c t g α ) = 1 1 + α 2	— ∞ ≤ α ≤ + ∞ , cos ( a r c c t g α ) = 1 1 + α 2
— 1 α 1 , t g ( a r c sin α ) = α 1 — α 2	α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , t g ( a r c cos α ) = 1 — α 2 α	— ∞ ≤ α ≤ + ∞ , t g ( a r c t g α ) = α	α ≠ 0 , t g ( a r c c t g α ) = 1 α
α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , c t g ( a r c sin α ) = 1 — α 2 α	— 1 α 1 , c t g ( a r c cos α ) = α 1 — α 2	α ≠ 0 , c t g ( a r c t g α ) = 1 α	— ∞ ≤ α ≤ + ∞ , c t g ( a r c c t g α ) = α

Теперь разберем примеры, как они применяются в задачах.

Вычислите косинус арктангенса из 5 .

Решение

У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2

Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6

Вычислить синус арккосинуса 1 2 .

Решение

Для этого нам понадобится формула: sin ( a r c cos α ) = 1 — a 2

Подставляем в нее значения и получаем: sin ( a r c cos 1 2 ) = 1 — ( 1 2 ) 2 = 3 2

Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2

Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.

Доказательства формул синусов арккосинуса, арккотангенса и арктангенса

Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:

sin 2 α + cos 2 α = 1 1 + c t g 2 α = 1 sin 2 α

Вспомним, что t g α · c t g α = 1 . Из этого можно получить:

sin α = 1 — cos 2 α , 0 ≤ α ≤ π sin α = t g α 1 + t g 2 α , — π 2 α π 2 sin α = 1 1 + c t g 2 α , 0 α π

У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.

Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.

Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.

Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.

Все наши расчеты можно сформулировать более емко:

1. sin α = 1 — cos 2 α , 0 ≤ α ≤ π

Следовательно, sin ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) = 1 — a 2

1. sin α = t g α 1 + t g α , — π 2 α π 2 ,

Следовательно, sin ( a r c t g α ) = t g ( a r c t g α ) 1 + t g 2 ( a r c t g α ) = α 1 + α 2

1. sin α = 1 1 + c t g 2 α , 0 α π

Следовательно, sin ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2

Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.

Их мы выведем по имеющемуся шаблону:

1. Из cos α = 1 — sin 2 α , — π 2 ≤ α ≤ π 2 следует, что

cos ( a r c sin α ) = 1 — sin 2 ( a r c sin α ) = 1 — a 2

1. Из cos α = 1 1 + t g 2 α , — π 2 α π 2 следует, что
2. Из cos α = c t g α 1 + c t g 2 α , 0 α π cos ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2

следует, что cos ( a r c t g α ) = c t g ( a r c c t g α ) 1 + c t g 2 ( a r c c t g α ) = α 1 + α 2

Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса

1. Исходим из t g α = sin α 1 — sin 2 α , — π 2 α π 2 . Получаем t g ( a r c sin α ) = sin ( a r c sin α ) 1 — sin 2 ( a r c sin α ) = α 1 — α 2 при условии, что — 1 α 1 .
2. Исходим из t g α = 1 — cos 2 α cos α , α ∈ [ 0 , π 2 ) ∪ ( π 2 , π ] , получаем

t g ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) cos ( a r c c os α ) = 1 — α 2 α при условии α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) .

1. Исходим из t g α = 1 c t g α , α ∈ ( 0 , π 2 ) ∪ ( π 2 , π ) , получаем t g ( a r c c t g α ) = 1 c t g ( a r c c t g α ) = 1 α при условии, что α ≠ 0 .

Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:

c t g α = 1 t g α

Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.

Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее

Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.

Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:

a r c sin α = a r c cos 1 — α 2 , 0 ≤ α ≤ 1 — a r c cos 1 — a 2 , — 1 ≤ α 0 a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 a r c sin α = a r c c t g 1 — α 2 α , 0 α ≤ 1 a r c c t g 1 — α 2 α — π , — 1 ≤ α ≤ 0

А так мы выразим арккосинус через остальные обратные функции:

a r c cos α = a r c sin 1 — α 2 , 0 ≤ α ≤ 1 π — arcsin 1 — α 2 , — 1 ≤ α 0 a r c cos α = a r c t g 1 — α 2 α , 0 α ≤ 1 π + arctg 1 — α 2 α , — 1 α 0 arccosα = arcctg α 1 — α 2 , — 1 α 1

Формула выражения арктангенса:

a r c t g α = a r c sin α 1 + α 2 , — ∞ α + ∞ a r c t g α = a r c cos 1 1 + α 2 , α ≥ 0 — a r c cos 1 1 + α 2 , α 0 a r c t g α = a r c c t g 1 α , α ≠ 0

Последняя часть – выражение арккотангенса через другие обратные функции:

a r c c t g α = a r c sin 1 1 + α 2 , α ≥ 0 π — a r c sin 1 1 + α 2 , α 0 a r c c t g α = a r c cos α 1 + α 2 , — ∞ α + ∞ a r c c t g α = a r c t g 1 α , α ≠ 0

Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.

Возьмём a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 и постараемся вывести доказательство.

Мы знаем, что a r c t g α 1 — α 2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:

sin ( a r c t g α 1 — α 2 ) = α 1 — α 2 1 + ( α 1 — α 2 ) 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 1 — α 2 = α

Получается, что a r c t g α 1 — α 2 при условии 1 a 1 – это и есть арксинус числа a .

Вывод: a r c sin a = a r c t g a 1 — a 2 , — 1 a 1

Прочие формулы доказываются по аналогии.

В завершение разберем один пример применения формул на практике.

Условие Вычислить синус арккотангенса минус корня из 3 .

Решение

Нам понадобится формула выражения арккотангенса через арксинус: a r c c t g α = a r c sin 1 1 + a 2 , α ≥ 0 π — arcsin 1 1 + a 2 , α 0
Подставим в нее α = — 3 и получим ответ – 1 2 . Непосредственное вычисление дало бы нам те же результаты: sin ( a r c c t g ( — 3 ) ) = sin 5 π 6 = 1 2 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sin α = 1 1 + c t g 2 α , 0 α π

В итоге у нас бы вышло: sin ( a r c c t g ( — 3 ) ) = 1 1 + c t g 2 ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2

Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin ( a r c c t g α ) = 1 1 + α 2 sin ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2

Прочие формулы с обратными функциями

Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.

Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:

sin 2 α 2 = 1 — cos α 2

Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:

sin α 2 = 1 — cos α 2

Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:

sin a r c cos α 2 = 1 — cos ( a r c cos α ) 2 ⇔ sin a r c cos α 2 = 1 — α 2

Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:

a r c cos α 2 = a r c sin 1 — α 2

Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.

В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Источник