Как вывести число эйлера

«Популярное изложение»: Число Эйлера и наши финансы. Краткое знакомство с константой «е»

Что общего у наших денег и числа Эйлера?

В то время как у числа π (пи) есть вполне определенный геометрический смысл и его использовали еще древние математики, то число е (число Эйлера) заняло свое заслуженное место в науке сравнительно недавно и корни его уходят прямиком… к финансовым вопросам.

С момента изобретения денег прошло совсем немного времени, когда люди догадались, что валюту можно одалживать или ссужать под определенный процент. Естественно, «древние» бизнесмены не пользовались привычным нам понятием «процент», но увеличение суммы на какой-то определенный показатель за установленный период времени было им знакомо.

На фото: банкнота стоимостью 10 франков с изображением Леонарда Эйлера (1707-1783).

Пытаясь высчитать, за сколько времени сумма, одолженная, допустим, под 20% годовых увеличится вдвое, люди уже начинали наощупь отыскивать путь, который в конечном итоге привел к определению числа е.

Мы не будем углубляться в пример с 20% годовых, так как от него добираться до числа Эйлера слишком долго. Воспользуемся самым распространенным и наглядным объяснением значения этой константы, а для этого нам придется немного пофантазировать и вообразить, что какой-то банк предлагает нам положить деньги на депозит под 100% годовых.

Мысленно-финансовый эксперимент

Для этого мысленного эксперимента можно взять любую сумму и результат всегда будет идентичным, но именно начиная с 1, мы сможем прийти непосредственно к первому приближенному значению числа е. Потому, допустим, что мы вкладываем в банк 1 доллар, при ставке 100% годовых в конце года у нас будет 2 доллара.

Но это только если проценты капитализируются (прибавляются) раз в год. А что если они будут капитализироваться два раза в год? То есть будет начисляться по 50% каждые полгода, причем вторые 50% будут начисляться уже не от начальной суммы, а от суммы, увеличенной на первые 50%. Будет ли это выгоднее для нас?

Наглядная инфографика, отображающая геометрический смысл числа π.

Разумеется, будет. При капитализации два раза в год, спустя полгода у нас будет 1,50 доллара на счете. К концу года прибавится еще 50% от 1,50 доллара, то есть общая сумма составит 2,25 доллара. Что же будет, если капитализацию проводить каждый месяц?

Нам будут начислять по 100/12% (то есть, примерно по 8,(3)%) каждый месяц, что окажется еще более выгодным – к концу года у нас будет 2,61 доллара. Общая формула для вычисления итоговой суммы при произвольном количестве капитализаций (n) в год выглядит так:

Итоговая сумма = 1(1+1/n) n

Получается, при значении n = 365 (то есть, если наши проценты будут капитализироваться каждый день), мы получим вот такую формулу: 1(1+1/365) 365 = 2,71 доллара. Из учебников и справочников мы знаем, что е приблизительно равно 2,71828, то есть, рассматривая ежедневную капитализацию нашего сказочного вклада мы уже подошли к приблизительному значению е, которое уже достаточно для многих вычислений.

Рост n можно продолжать бесконечно и чем больше будет его значение, тем точнее мы сможем вычислить число Эйлера, вплоть до необходимого нам, по какой-либо причине, знака после запятой.

Это правило, конечно, не ограничивается только нашими финансовыми интересами. Математические константы далеко не «узкие специалисты» – они действуют одинаково хорошо вне зависимости от области применения. Поэтому хорошенько покопавшись, можно обнаружить их практически в любой сфере жизни.

Получается, число е что-то вроде меры всех изменений и «натуральный язык математического анализа». Ведь «матан» крепко повязан с понятиями дифференцирования и интегрирования, а обе эти операции имеют дело с бесконечно малыми изменениями, которые так великолепно характеризует число е.

Уникальные свойства числа Эйлера

Рассмотрев самый доходчивый пример объяснения построения одной из формул для вычисления числа е, кратко рассмотрим еще пару вопросов, которые к нему напрямую относятся. И один из них: что же такого уникального в числе Эйлера?

По идее, абсолютно любая математическая константа уникальна и у каждой есть своя история, но, согласитесь, претензия на звание натурального языка математического анализа – довольно весомая претензия.

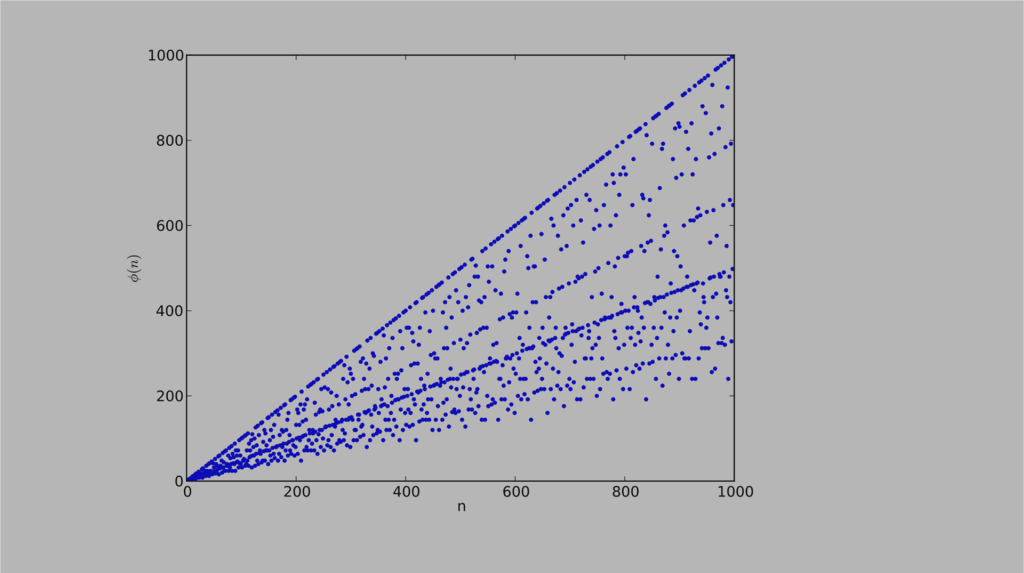
Первая тысяча значений ϕ (n) для функции Эйлера.

Однако, у числа е есть на то основания. При построении графика функции y = e x выясняется поразительный факт: не только y равен e x , этому же показателю равен градиент кривой и площадь под кривой. То есть площадь под кривой от определенного значения y до минус бесконечности.

Никакое другое число этим похвастаться не может. Нам, гуманитариям (ну, или просто НЕ математикам), такое заявление мало что говорит, но сами математики утверждают, что это очень важно. Почему важно? Мы попробуем разобраться в этом вопросе в другой раз.

Логарифм, как предпосылка Числа Эйлера

Возможно, кто-то помнит со школы, что число Эйлера – это также основание натурального логарифма. Что ж, это согласуется с его природой, как меры всех изменений. Все-таки, причем же тут Эйлер? Справедливости ради нужно отметить, что е также иногда называется числом Непера, но без Эйлера история будет неполной, как и без упоминания о логарифмах.

Изобретение в XVII веке логарифмов шотландским математиком Джоном Непером стало одним из важнейших событий истории математики. На праздновании в честь юбилея этого события, которое прошло в 1914 году Лорд Мултон (Lord Moulton) так отозвался о нем:

«Изобретение логарифмов было для научного мира как гром среди ясного неба. Никакая предшествующая работа не вела к нему, не предсказывала и не обещала это открытие. Оно стоит особняком, оно прорывается из человеческой мысли внезапно, не заимствуя ничего из работы других разумов и не следуя уже известным тогда направлениям математической мысли».

Пьер-Симон Лаплас, знаменитый французский математик и астроном, еще более драматично выразил важность этого открытия: «Изобретение логарифмов, уменьшив часы кропотливого труда, вдвое увеличило жизнь астронома». Что же так впечатлило Лапласа? А причина очень проста – логарифмы позволили ученым в разы уменьшить время, обычно затрачиваемое для громоздких вычислений.

В общем и целом, логарифмы упрощали вычисления – опускали их на один уровень ниже по шкале сложности. Проще говоря, вместо умножения и деления приходилось совершать операции сложения и вычитания. А это намного эффективнее.

е – основание натурального логарифма

Давайте примем за данность тот факт, что Непер был первопроходцем в сфере логарифмов – их изобретателем. По крайней мере, он опубликовал свои открытия первым. В таком случае возникает вопрос: в чем заслуга Эйлера?

Все просто – его можно назвать идейным наследником Непера и человеком, который довел дело жизни шотландского ученного до логарифмического (читать логического) завершения. Интересное такое вообще возможно?

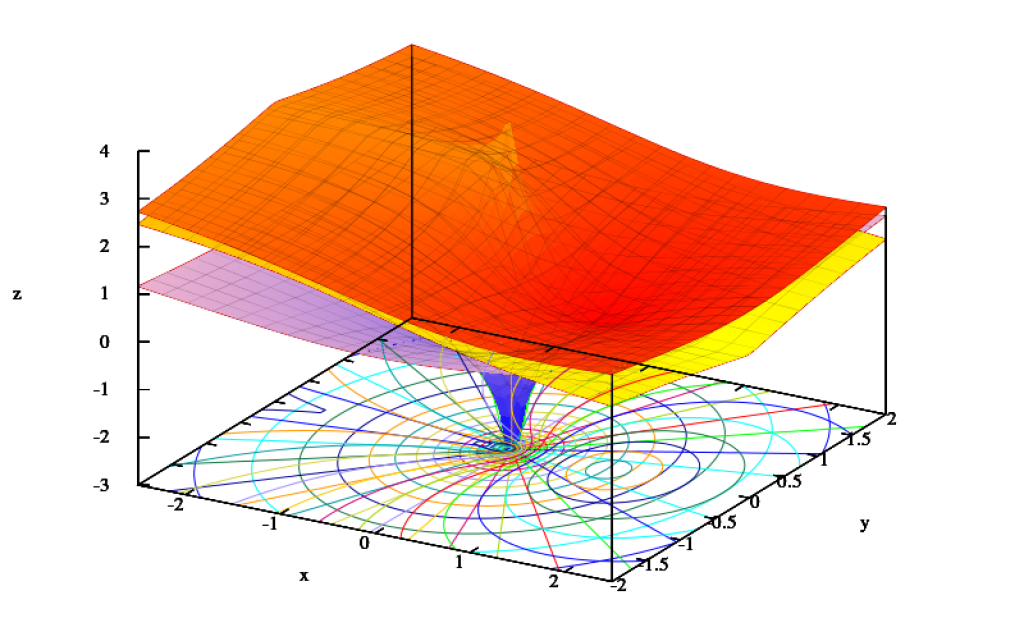
Какой-то очень важный график построенный при помощи натурального логорифма.

Если говорить конкретнее, то Эйлер вывел основание натурального логарифма, теперь известное как число е или число Эйлера. Кроме этого, он вписал свое имя в историю науки столько раз, сколько и не снилось Васе, который, кажется, успел «побывать» везде.

К сожалению, конкретно принципы работы с логарифмами – это тема отдельной большой статьи. Поэтому пока будет достаточно сказать, что благодаря работе ряда самоотверженных ученых, которые, буквально, посвятили годы своей жизни составлению логарифмических таблиц в те времена, когда никто и слыхом не слыхивал о калькуляторах, прогресс науки сильно ускорился.

На фото: Джон Непер — шотландский математик, изобретатель логарифма (1550—1617.)

Забавно, но этот прогресс, в конце концов, привел к выходу из употребления данных таблиц, а причиной тому послужило именно появление ручных калькуляторов, которые полностью переняли на себя задачу по выполнению такого рода вычислений.

Возможно, вы еще слышали о логарифмических линейках? Когда-то без них инженерам или математикам бывало не обойтись, а сейчас это почти как астролябия – интересный инструмент, но скорее в плане истории науки, чем повседневной практики.

Почему так важно быть основанием логарифма?

Оказывается, основанием логарифма может быть любое число (например, 2 или 10), но, именно благодаря уникальным свойствам числа Эйлера логарифм по основанию е называется натуральным. Он как бы встроен в структуру реальности – от него никуда не убежать, да и не нужно, ведь он значительно упрощает жизнь ученым, работающим в самых разных областях.

Приведем доходчивое объяснение природы логарифма с сайта Павла Бердова. Логарифм по основанию a от аргумента x – это степень, в которую надо возвести число a, чтобы получить число x. Графически это обозначается так:

log_a x = b, где a – основание, x – аргумент, b – это то, чему равен логарифм.

Например, 2 3 = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен 3-м, поскольку 2 3 = 8).

Выше мы видели число 2 в образе основания логарифма, но математики говорят, что самый талантливый актер на эту роль – число Эйлера. Поверим им на слово… А потом проверим, чтобы убедиться самим.

Выводы

Наверное, плохо, что в рамках высшего образования так сильно разделены естественные и гуманитарные науки. Иногда это приводит к слишком сильному «перекосу» и получается так, что с человеком, прекрасно разбирающимся, допустим, в физике и математике, абсолютно неинтересно говорить на другие темы.

И наоборот, можно быть первоклассным специалистом-литературоведом, но, в то же время, быть совершенно беспомощным, когда речь заходит о той же физике и математике. А ведь все науки интересны по-своему.

Надеемся, что мы, пытаясь преодолеть свою собственную ограниченность в рамках импровизированной программы «я – гуманитарий, но я лечусь», помогли и вам узнать и, главное, понять, что-то новое из не совсем привычной научной сферы.

Ну а тем, кто захочет поподробнее узнать о числе Эйлера, можем порекомендовать несколько источников, в которых может при желании разобраться даже далекий от математики человек: Эли Маор в своей книге «е: история одного числа» («e: the story of a number») подробно и доступно описывает предысторию и историю числа Эйлера.

Также, в разделе «Рекомендуем« под этой статьей Вы сможете название youtube-каналов и видео, которые были сняты профессиональными математиками, пытающимися доходчиво объяснить число Эйлера так, чтобы это было понятно даже не специалистам Русские субтитры в наличие.

Источник

Число e – его смысл и доказательство сходимости последовательности

Определение числа e

Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.

Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).

Смысл числа e

С развитием механики, возникла потребность в вычислении мгновенной скорости движения тел. Для определения скорости v , мы должны взять разность значений координат x в два момента времени и разделить на промежуток времени между ними:
.
По этой формуле, однако, мы не получим мгновенного значения скорости, а получим ее среднее значение в промежутке времени между и . Чтобы найти мгновенную скорость, мы должны положить . Но тогда знаменатель дроби станет равным нулю. Таким образом, эта задача не решается методами классической алгебры.

При попытке решить эту задачу, возникла новая математическая дисциплина – математический анализ. В нем, мгновенная скорость в момент времени t определяется как предел, к которому стремится отношение при , стремящемся к нулю. Этот предел называется производной x по t .

Таким образом, производная является одним из самых важных понятий в математическом анализе. Поэтому необходимо уметь вычислять производные. Оказывается, что если мы найдем производную показательной функции , то ее вычисление сводится к вычислению второго замечательного предела, аналогичного пределу последовательности (1), и выражается через число e :
.

Тогда, если за основание степени a взять число e , то производная будет иметь наиболее простой вид:
.
В связи с этим, в математическом анализе, за основание степени, там где это возможно, выбирают именно число e . Показательная функция с основанием e называется экспонентой. Логарифм по основанию e называется натуральным логарифмом и имеет специальное обозначение . Любую другую показательную функцию (с другим основанием) можно выразить через экспоненту:
.

Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.

Но прежде, чем применять число e , нужно доказать, что оно существует. То есть нужно доказать, что существует конечный предел последовательности при n стремящемся к бесконечности: .

Доказательство сходимости последовательности

Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.

Доказательство можно выполнять различными способами.

Применение бинома Ньютона

Рассмотрим последовательность с общим членом
(2) .
Докажем, что она строго возрастает. Для этого применим формулу бинома Ньютона:

Здесь

– биноминальные коэффициенты.

Подставим и выполним преобразования. Тогда элемент запишется в виде суммы положительных членов:

.
Выполняя деление в каждом члене на , имеем:
(3)

Для элемента имеем сумму положительных членов:

Далее замечаем, что

Таким образом, каждый член в , начиная с третьего по n + 1 -ый, больше соответствующего члена в . Кроме этого, в на один положительный член больше. Поэтому

То есть последовательность строго возрастает.

Докажем, что эта последовательность ограничена. Поскольку она возрастает, то снизу она ограниченна значением . Докажем, что последовательность ограничена сверху. Для этого замечаем, что

Тогда

Далее замечаем, что . Тогда
.
Применим формулу суммы членов геометрической прогрессии:
.

Отсюда получаем ограниченность :
.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Применение неравенства Бернулли

Снова рассматриваем последовательность
(2) .
Докажем ее монотонность и ограниченность применяя неравенство Бернулли. При и при натуральном , имеет место следующее неравенство:
(4) .

Докажем с его помощью, что последовательность строго возрастает. Выпишем ее элементы в следующем виде:
, .
Тогда
.
Преобразуем второй множитель и применим неравенство Бернулли:

;
.
Поскольку , то строгое возрастание последовательности доказано.

Докажем, что последовательность ограничена. Поскольку она возрастает, то нам нужно доказать ее ограниченность сверху. Для четных n , является натуральным числом. Имеем:

;
.
Отсюда следует, что элементы последовательности с четными номерами ограничены:
.
Если n нечетно, то используем тот факт, что последовательность строго возрастает. Тогда четно. Поэтому и при нечетных n , элементы последовательности ограничены:
.

Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.

Использование вспомогательной последовательности

Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.

В нашем случае, для исследования сходимости последовательности
(2) ,
возьмем вспомогательную последовательность
(5) .

Покажем, что она строго убывает. Для этого используем неравенство Бернулли:
(4) .
Имеем:
;

.
Поскольку , то отсюда следует, что последовательность строго убывает.

Покажем, что ограничена. Поскольку она убывает, то сверху она ограничена значением . Покажем, что последовательность ограничена снизу. Снова применяем неравенство Бернулли:
;
.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 25-03-2019

Источник