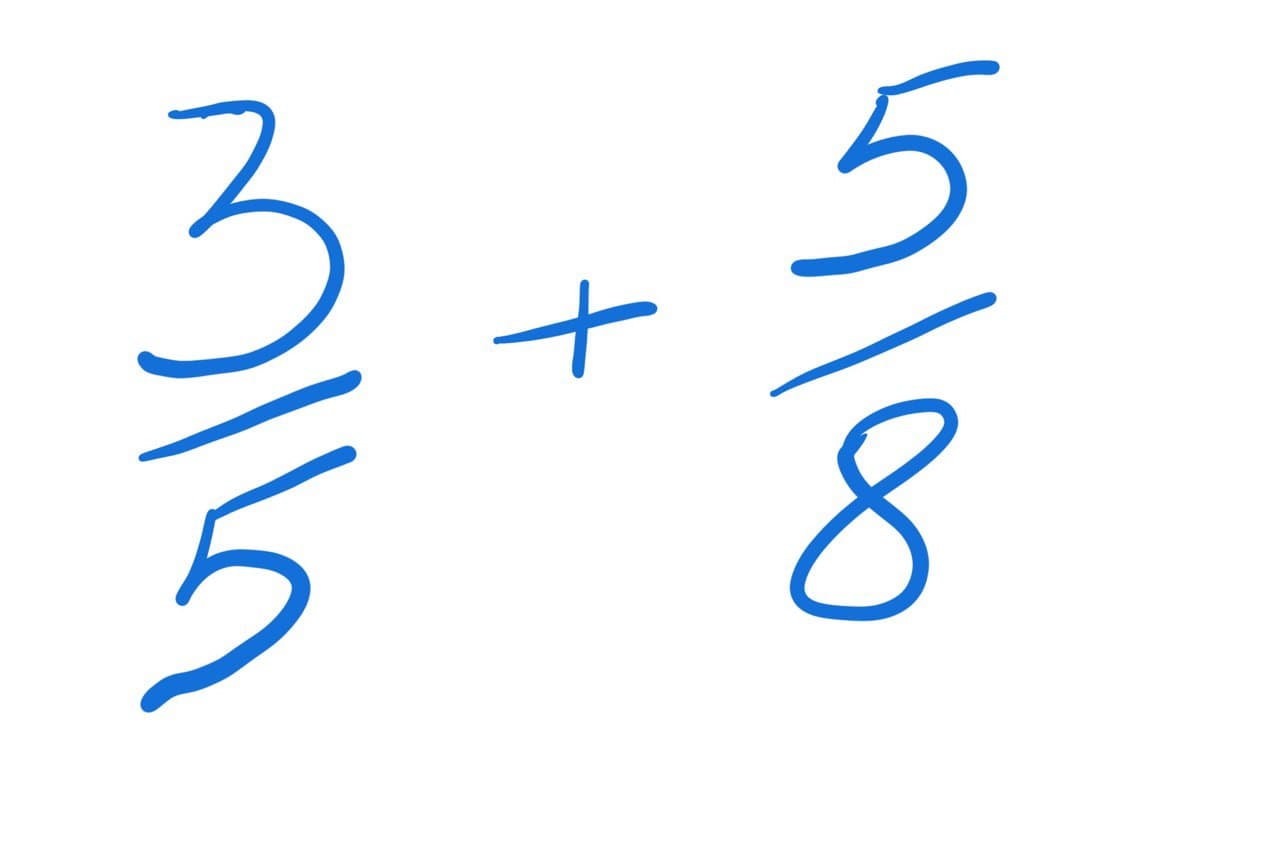Как вывести делители числа java

Занятие 7. Циклы в Java

Цикл — это многократно повторяющийся фрагмент программы.

В java существует два типа циклов: типа «пока» и типа «n-раз».

Первый тип «пока» предназначен для повторения какого-то действия до тех пор, пока выполняется некоторое условие. Пример: увеличивать число на 5 до тех пор, пока оно не станет трёхзначным.

Второй тип «n-раз» предназначен для повторения каких-то действий заранее известное количество раз. Пример: умножить число само на себя 4 раза.

Цикл типа «пока» (операторы while и do…while)

Оператор while повторяет указанные действия до тех пор, пока его параметр имеет истинное значение.

Например, такой цикл выполнится 4 раза, а на экран будет выведено «1 2 3 4 »:

Такой цикл не выполнится ни разу и на экран ничего не выведется:

Такой цикл будет выполняться бесконечно, а на экран выведется «1 2 3 4 5 6 7 …»:

Условие, определяющее будет ли цикл повторятся снова, проверяется перед каждым шагом цикла, в том числе перед самым первым. Говорят, что происходит предпроверка условия.

Бывает цикл типа «пока» с постпроверкой условия. Для его записи используется конструкция из операторов do…while.

Такой цикл выполнится 4 раза, а на экран будет выведено «2 3 4 5 »:

Такой цикл выполнится 1 раз, а на экран будет выведено «2 »:

Тело цикла do…while выполняется по крайней мере один раз. Этот оператор удобно использовать, когда некоторое действие в программе нужно выполнить по крайней мере единожды, но при некоторых условиях придётся повторять его многократно.

Ознакомьтесь со следующей программой (она загадывает случайное целое число из отрезка [1;10] и просит пользователя его угадать, вводя варианты с клавиатуры, пока пользователь не угадает число, программа будет ему подсказывать, сообщая больше или меньше число загаданное, чем то, что ввёл пользователь):

Внесите в программу следующие доработки:

Программа должна считать количество попыток, которое потребовалось пользователю, чтобы угадать число. И в конце сообщать, сколько было попыток.

Программа должна загадывать число не из отрезка [1;10], а целое число из отрезка от [−10;10], исключая ноль. При этом, постарайтесь, чтобы распределение случайных чисел генерируемых программой было равномерных (т. е. в случае выпадения нуля его нельзя просто заменить на какое-то другое число, например, на 1, ведь тогда 1 будет выпадать с вдвое большей вероятностью, чем остальные числа).

Программа должна подсказывать пользователю, что он ошибся в знаке, если программа загадала положительное число, а пользователь ввёл отрицательное. И наоборот.

Цикл типа «n-раз» (оператор for)

Оператор for содержит три параметра. Первый называется инициализацией, второй — условием повторения, третий — итерацией.

В первом параметре обычно выбирают какую-то переменную, с помощью которой будет подсчитываться количество повторений цикла. Её называют счетчиком. Счётчику задают некоторое начальное значение (указывают, начиная с какого значения он будет изменяться).

Во втором параметре указывают некоторое ограничение на счётчик (указывают, до какого значения он будет изменяться).

В третьем параметре указывают выражение, изменяющее счётчик после каждого шага цикла. Обычно это инкремент или декремент, но можно использовать любое выражение, где счётчику будет присваиваться некоторое новое значение.

Перед первым шагом цикла счётчику присваивается начальное значение (выполняется инициализация). Это происходит лишь однажды.

Перед каждым шагом цикла (но после инициализации) проверяется условие повторения, если оно истинно, то в очередной раз выполняется тело цикла. При этом, тело цикла может не выполниться ни разу, если условие будет ложным в момент первой же проверки.

После завершения каждого шага цикла и перед началом следующего (и, значит, перед проверкой условия повторения) выполняется итерация.

Представленная программа выводит на экран числа от 1 до 100:

Представленная программа выводит на экран числа от 10 до −10:

Представленная программа выводит на экран нечётные числа от 1 до 33:

Представленная программа вычислит сумму элемнтов фрагмента последовательности 2, 4, 6, 8,… 98, 100. Итак:

Представленная программа будет возводить число из переменной a в натуральную степень из переменной n:

Представленная программа выведет на экран 10 первых элементов последовательности 2n+2, где n=1, 2, 3…:

Представленная программа выведет на экран 10 первых элементов последовательности 2a_n−1+3, где a₁=3:

В одном цикле можно задавать сразу несколько счётчиков. При этом несколько выражений в итерации и в инициализации разделяются запятыми. Условие повторения можно задавать только одно, но оно может быть выражением, содержащим сразу несколько счётчиков.

Представленная программа выведет на экран 10 первых элементов последовательности 2a_n−1–2, где a₁=3:

Представленная программа выведет на экран такую последовательность «0 -1 -4 -9 -16 -25»:

Досрочное завершение цикла (оператор break)

Как цикл типа «пока» так и цикл типа «n-раз» можно завершить досрочно, если внутри тела цикла вызвать оператор break. При этом произойдёт моментальный выход из цикла, не будет закончен даже текущий шаг (т. е. если после break присутствовали какие-то ещё операторы, то они не выполнятся).

В результате работы следующего примера на экран будут выведены только числа «1 2 3 4 Конец»:

Когда программа будет выполнять цикл в пятый раз(войдёт в цикл с счётчиком равным 5), сразу же будет проверено и окажется истинным условие при котором выполнится оператор break. Оставшаяся часть тела цикла (вывод на экран) уже производится не будет: программа сразу перейдёт к выполнению операций указанных после цикла и далее.

C помощью оператор break можно прервать заведомо бесконечный цикл. Пример (на экран выведется «100 50 25 12 6 3 1 0 » и после этого цикл остановится):

Оператор break имеет смысл вызывать только при наступлении какого-то условия, иначе цикл будет завершен досрочно на первом же своём шаге.

В представленном выше примере вывода в цикле на экран не произойдёт ни разу, а когда переменная a выведется на экран после цикла, то окажется, что её значение ни разу не менялось, т. е. выведено будет «a=25» (и ничего больше).

Обратите внимание также на то, что переменная была объявлена до начала цикла. Когда переменная объявляется в параметрах цикла, то она оказывается недоступной за его приделами, а в данном случае требовалось иное — узнать какое значение будет у счётчика после завершенияцикла.

Задачи

Создайте программу, выводящую на экран все четырёхзначные числа последовательности 1000 1003 1006 1009 1012 1015 ….

Создайте программу, выводящую на экран первые 55 элементов последовательности 1 3 5 7 9 11 13 15 17 ….

Создайте программу, выводящую на экран все неотрицательные элементы последовательности 90 85 80 75 70 65 60 ….

Создайте программу, выводящую на экран первые 20 элементов последовательности 2 4 8 16 32 64 128 ….

Выведите на экран все члены последовательности 2a_n-1–1, где a₁=2, которые меньше 10000.

Выведите на экран все двузначные члены последовательности 2a_n-1+200, где a₁= –166.

Создайте программу, вычисляющую факториал натурального числа n, которое пользователь введёт с клавиатуры.

Выведите на экран все положительные делители натурального числа, введённого пользователем с клавиатуры.

Проверьте, является ли введённое пользователем с клавиатуры натуральное число — простым. Постарайтесь не выполнять лишних действий (например, после того, как вы нашли хотя бы один нетривиальный делитель уже ясно, что число составное и проверку продолжать не нужно). Также учтите, что наименьший делитель натурального числа n, если он вообще имеется, обязательно располагается в отрезке [2; √n].

Создайте программу, выводящую на экран 12 первых элементов последовательности 2a_n-2–2, где a₁=3 и a₂=2.

Выведите на экран первые 11 членов последовательности Фибоначчи. Напоминаем, что первый и второй члены последовательности равны единицам, а каждый следующий — сумме двух предыдущих.

Для введённого пользователем с клавиатуры натурального числа посчитайте сумму всех его цифр (заранее не известно сколько цифр будет в числе).

В городе N проезд в трамвае осуществляется по бумажным отрывным билетам. Каждую неделю трамвайное депо заказывает в местной типографии рулон билетов с номерами от 000001 до 999999. «Счастливым» считается билетик у которого сумма первых трёх цифр номера равна сумме последних трёх цифр, как, например, в билетах с номерами 003102 или 567576. Трамвайное депо решило подарить сувенир обладателю каждого счастливого билета и теперь раздумывает, как много сувениров потребуется. С помощью программы подсчитайте сколько счастливых билетов в одном рулоне?

В городе N есть большой склад на котором существует 50000 различных полок. Для удобства работников руководство склада решило заказать для каждой полки табличку с номером от 00001 до 50000 в местной типографии, но когда таблички напечатали, оказалось что печатный станок из-за неисправности не печатал цифру 2, поэтому все таблички, в номерах которых содержалась одна или более двойка (например, 00002 или 20202) — надо перепечатывать. Напишите программу, которая подсчитает сколько всего таких ошибочных табличек оказалось в бракованной партии.

Электронные часы показывают время в формате от 00:00 до 23:59. Подсчитать сколько раз за сутки случается так, что слева от двоеточия показывается симметричная комбинация для той, что справа от двоеточия (например, 02:20, 11:11 или 15:51).

В американской армии считается несчастливым число 13, а в японской — 4. Перед международными учениями штаб российской армии решил исключить номера боевой техники, содержащие числа 4 или 13 (например, 40123, 13313, 12345 или 13040), чтобы не смущать иностранных коллег. Если в распоряжении армии имеется 100 тыс. единиц боевой техники и каждая боевая машина имеет номер от 00001 до 99999, то сколько всего номеров придётся исключить?

Источник

Наибольший простой делитель числа в Java

Я пытаюсь найти наибольший простой множитель числа при решении этой проблемы здесь . Я думаю, что все делаю правильно, однако один из тестовых примеров (№2) дает сбой, и я не могу придумать ни одного углового случая, когда он мог бы потерпеть неудачу. Вот мой код, пожалуйста, посмотрите и попробуйте что-нибудь найти.

В основном то, что я делаю:

5 ответов

Кажется, у вас есть какая-то ошибка в вашем коде, как при вводе функции 16 largePrime , возвращающей 1., и это верно, когда ввод является степенью 3.

Почему вы удаляете числа, кратные 2, и кратные 3? Таким образом, если у вас есть число, которое представляет собой любую комбинацию степеней 2 и 3, вы получите ответ как 1, что явно неверно.

Для этой проблемы вы можете сделать простой способ перехода от 2 к sqrt (n) и сохранить наибольшее число, которое делит n, когда вы закончите цикл, просто верните наивысший найденный делитель.

Вот один из простых способов извлечения простых множителей:

Эти первые петли — проблема. Они уменьшат все четные числа до 1 , таким образом пропуская 2 в качестве множителя. Изменение кода для использования:

У вас все еще есть другие проблемы — например, вы сообщаете, что наибольший простой множитель 25 равен 25 , а наибольший простой множитель 49 равен 49 .

Просто запустите этот код, используя свой и мой, чтобы узнать, где ваш:

1 отбросьте цикл для 2 и 3. Если нет, вы не получите 2, 2×2, 3, 2×3, . все кратные 2 и 3

2 измените свой цикл, чтобы он остановился на 2 (а не на 5):

5 циклов до sqrt (n) с 1

Подробное описание алгоритма: вы можете сделать это, сохраняя три переменные: число, которое вы пытаетесь разложить на множители (A) текущее хранилище делителей (B) наибольшее хранилище делителей (C) Первоначально пусть (A) будет числом, которое вас интересует — в данном случае это 600851475143. Тогда пусть (B) равно 2. Имейте условие, которое проверяет, делится ли (A) на (B). Если он делится, разделите (A) на (B), сбросьте (B) на 2 и вернитесь к проверке, делится ли (A) на (B). Иначе, если (A) не делится на (B), увеличьте (B) на +1, а затем проверьте, делится ли (A) на (B). Выполняйте цикл до тех пор, пока (A) не станет 1. Возвращаемое (3) будет наибольшим простым делителем 600851475143.

Источник

Подсчитайте количество делителей для всех чисел до N

Мне нужно подсчитать все делители для каждого числа в диапазоне 1 to n . Ниже я написал реализацию, поскольку для данного целого числа num оно подсчитывает количество делителей num . Его сложность равна O(sqrt(n)) . Таким образом, вся сложность оказывается O(n * sqrt(n)) . Можно ли его уменьшить? Если ДА, то можете ли вы дать алгоритм для этого?

КОД :

PS:
Эта функция будет вызываться n раз.

2 ответа

Вы можете улучшить наивный подход, используя своего рода обобщенное Сито Эратосфена. Вместо того, чтобы просто отмечать число как составное, сохраните его первый найденный вами делитель (я делаю это в функции computeDivs ниже).

Вы также можете увидеть код, выполненный на ideone, здесь.

Короче говоря, я использую сито для вычисления наибольшего простого множителя для каждого числа. Используя это, я могу очень эффективно вычислить факторное разложение каждого числа (и я использую это в countDivisors).

Трудно вычислить сложность решета, но стандартная оценка равна O(n * log(n)) . Также я довольно уверен, что эту сложность улучшить невозможно.

Вы можете добиться большего, чем O(n.sqrt(n)) , используя простую итерацию. Код написан на C ++, но вы легко можете понять суть.

Время выполнения равно n/1 + n/2 + n/3 + n/4 + . + n/n , которое может быть приблизительно равно O(nH(n)) , где H(n) — это гармонический ряд. Думаю, значение не больше O(nlog(n)) .

Источник

Как вывести делители числа java

Мы уже не раз складывали два простых числа, две десятичные дроби или даже простое число с десятичной дробью. Однако мир состоит не только из примитивных данных, порой нам приходится работать и с дробями, с обыкновенными дробями.

Обыкновенные дроби #

сложение дробей

Обыкновенная дробь, как мы знаем из школы, состоит из двух частей: верхней и нижней. Это если не считать чёрточку посередине за часть дроби. Верхнюю часть дроби в математике принято называть числитель, а нижнюю часть знаменатель. В английском соответственно numerator и denominator.

Для того, что бы мы могли проводить математические операции с дробями мы должны привести их к общему знаменателю и научиться сокращать их. Для этого нам нужно вспомнить про НОД и НОК.

НОД — наибольший общий делитель #

Greatest common divisor — GCD.

НОД´ом для чисел 25 и 15 является 5. Это наибольший общий делитель двух этих чисел. Для чисел 9 и 15 НОД´ом является 3. Оба числа делятся на 3 без остатка. И три является наибольшим общим делителем.

Математика древняя наука и впервые НОД был описан Евклидом в третьем веке до нашей эры. Алгоритм нахождения назван в его честь — Алгори́тм Евкли́да.
В Java Алгоритм Евклида будет реализован вот так:

Этот алгоритм в цикле занимается вычитанием от одной переменной другой и в итоге находит нод. если задуматься, то “бесконечное” вычитание пока A не сравняется с B это деление с нахождением остатка деления. Сегодня у нас есть оператор модуло и мы можем “усовершенствовать” алгоритм:

Этот же алгоритм мы можем решить с применением рекурсии, мы должны прописать условие выхода и само решение:

Это не единственные способы решения. Всегда ещё можно решить бинарным поиском. Но думаю на этом мы пока уже можем остановиться и сказать, что НОД мы находить научились и можем попробовать найти НОК.

НОК — Наименьшее общее кратное #

Least common multiple — LCM

НОК — это произведение наших двух чисел и делении его на НОД. Реализуется это вот так:

Теперь мы попробуем реализовать правильное “поведение” дробей.

Источник

Читайте также:  Как стирать кофту с белыми воротниками