Как вывести десятичную степень

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень — это вычисление значения степени некоторого числа.

То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите — 2 в степень 4 .

Решение

Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , ( — 2 , 56 ) 0 = 1 2 3 0 = 1

0 0 — не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 2 в степень — 3 .

Решение

Используя определение выше, запишем: 2 — 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень — 2 .

Решение

Переформулируем: 1 , 43 — 2 = 1 ( 1 , 43 ) 2

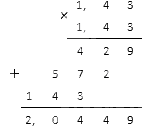
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло ( 1 , 43 ) — 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: ( 1 , 43 ) — 2 = 10000 20449

Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 — 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2

После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную — значения не имеет: 0 — 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .

Источник

Таблица степеней

О чем эта статья:

Основные понятия

Степень числа — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.

Показатель степени всегда натуральное число — это значит, что его можно использовать при счете или перечислении предметов:

• a n = a * a *. * a, где a — основание степени,
• n — натуральный показатель степени.

Запись читается, как «a» в степени «n».

Вот пример для наглядности:

• 3 5 = 3 * 3 * 3 * 3 * 3 = 243

Эту запись можно прочитать тремя способами:

• 3 в 5 степени;
• пятая степень числа три;
• возвести число три в пятую степень.

Записывайся на математические курсы для учеников с 1 по 11 классы! Первое занятие — бесплатно!

Свойства степеней

Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.

(a * b) n = a n * b n

(a : b) n = a n : b n

Таблица степеней от 1 до 10

Таблица степеней — это перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Ниже приведены два вида таблиц, выберите ту, которая удобнее для вас — скачайте на телефон или распечатайте и положите в учебник.

Как найти необходимые значения в этой таблице:

• В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
• В первой строке находим показатель степени. Запомним найденный столбец.
• На пересечении строки и столбца находится ответ.

В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.

А если ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Вот несколько подходящих:

Алгебра — предмет серьезный: при переходе в новый класс багаж формул и правил будет только увеличиваться. Поэтому важно запоминать все последовательно и практиковаться на примерах.

Решение задач

Задание 1. Упростить и решить выражение 5 2 * 5 3 .

5 2 * 5 3 = 5 2+3 = 5 5 = 3125

Задание 2. Упростить и решить выражение 2 4 * 3 3 * 2 5 .

2 4 * 3 3 * 2 5 = 2 4+5 * 3 3 = 2 9 * 3 3 = 512 * 27 = 13824

Задание 3. Найти 36 4 .

При условии, что у нас есть только таблица до 10, разложим основание степени на множители:

36 4 = 6 4 * 6 4 = 1296 * 1296 = 1679616

36 4 = 6 4 * 6 4 = 6 8 = 1679616

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Степень десяти

Степени десяти , также называемые номерами шагов , являются степенями с основанием 10 и целой экспонентой. Важным применением степеней десяти является экспоненциальная запись чисел с плавающей запятой .

Оглавление

Сила десяти

Для числовых названий степеней десяти см. Также соответствующий раздел в числовых названиях . Вот самые важные числовые имена степеней десяти:

Фамилия	Число в экспоненциальной записи	Число в десятичной системе счисления
Квадриллионная	10 — 24 <\ displaystyle 10 ^ <- 24>>	0,000 000 000 000 000 000 000 001 <\ Displaystyle 0 <,>000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 001>
Триллионных	10 — 21-е <\ displaystyle 10 ^ <- 21>>	0,000 000 000 000 000 000 001 <\ Displaystyle 0 <,>000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 001>
Триллионный	10 — 18-е <\ displaystyle 10 ^ <- 18>>	0,000 000 000 000 000 001 <\ Displaystyle 0 <,>000 \, 000 \, 000 \, 000 \, 000 \, 001>
Бильярдстель	10 — 15-е <\ displaystyle 10 ^ <- 15>>	0,000 000 000 000 001 <\ displaystyle 0 <,>000 \, 000 \, 000 \, 000 \, 001>
Триллионный	10 — 12-е <\ displaystyle 10 ^ <- 12>>	0,000 000 000 001 <\ displaystyle 0 <,>000 \, 000 \, 000 \, 001>
миллиардный	10 — 9 <\ displaystyle 10 ^ <- 9>>	0,000 000 001 <\ displaystyle 0 <,>000 \, 000 \, 001>
Миллионный	10 — Шестой <\ displaystyle 10 ^ <- 6>>	0,000 001 <\ displaystyle 0 <,>000 \, 001>
Сто тысячных	10 — 5 <\ displaystyle 10 ^ <- 5>>	0,000 01 <\ displaystyle 0 <,>000 \, 01>
Десять тысячных	10 — 4-й <\ displaystyle 10 ^ <- 4>>	0,000 1 <\ displaystyle 0 <,>000 \, 1>
Тысячные	10 — 3 <\ displaystyle 10 ^ <- 3>>	0,001 <\ displaystyle 0 <,>001>
Сотые	10 — 2 <\ displaystyle 10 ^ <- 2>>	0 , 01 <\ displaystyle 0 <,>01>
десятый	10 — 1 <\ displaystyle 10 ^ <- 1>>	0 , 1 <\ displaystyle 0 <,>1>
один	10 0 <\ displaystyle 10 ^ <0>>	1 <\ displaystyle 1>
десять	10 1 <\ displaystyle 10 ^ <1>>	10 <\ displaystyle 10>
Сотня	10 2 <\ displaystyle 10 ^ <2>>	100 <\ displaystyle 100>
тысяча	10 3 <\ displaystyle 10 ^ <3>>	1 000 <\ displaystyle 1 \, 000>
Десять тысяч	10 4-й <\ displaystyle 10 ^ <4>>	10 000 <\ displaystyle 10 \, 000>
Сто тысяч	10 5 <\ displaystyle 10 ^ <5>>	100 000 <\ displaystyle 100 \, 000>
миллион	10 Шестой <\ displaystyle 10 ^ <6>>	1 000 000 <\ displaystyle 1 \, 000 \, 000>
миллиард	10 9 <\ displaystyle 10 ^ <9>>	1 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000>
триллион	10 12-е <\ displaystyle 10 ^ <12>>	1 000 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000 \, 000>
Бильярд	10 15-е <\ displaystyle 10 ^ <15>>	1 000 000 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000 \, 000 \, 000>
Триллион	10 18-е <\ displaystyle 10 ^ <18>>	1 000 000 000 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000>
Триллион	10 21-е <\ displaystyle 10 ^ <21>>	1 000 000 000 000 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000>
Квадриллион	10 24 <\ displaystyle 10 ^ <24>>	1 000 000 000 000 000 000 000 000 <\ Displaystyle 1 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000 \, 000>

Показатель степени указывает количество нулей в десятичной системе счисления степени десяти. Если он говорит 10 до шестого (10 6 ), то это миллион.

использовать

Поскольку наша обычная система счисления , десятичная система (от латинского decimus «десятый»), основана на степенях десяти, они подходят для компактного написания даже очень больших и очень маленьких чисел. Они составляют основу научной записи ( SCI, сокращенно от Scientific ), которая может уменьшить числа до представленной мантиссы и экспоненты по основанию 10.

В качестве примеров:

4,711 ⋅ 10 3 знак равно 4711 <\ displaystyle 4 <,>711 \ cdot 10 ^ <3>= 4711> 4,711 ⋅ 10 Шестой знак равно 4-й 711 000 <\ Displaystyle 4 <,>711 \ cdot 10 ^ <6>= 4 \, 711 \, 000> 0,000 000004711 знак равно 4,711 ⋅ 10 — 9 <\ displaystyle 0 <,>000000004711 = 4 <,>711 \ cdot 10 ^ <- 9>>

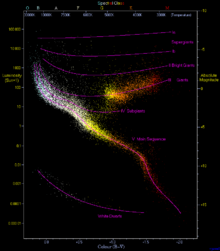
Оси диаграмм также часто делятся не линейно, а скорее на десятичные степени в логарифмической шкале, когда речь идет об очень больших диапазонах значений. Пример из астрономии, который связан с «астрономически большими числами», — это диаграмма Герцшпрунга-Рассела , которая на соседнем рисунке показывает по оси ординат шкалу от 0,00001 до 100 000 единиц солнечной светимости L ₀ . Но тогда з. B. посередине между 10 и 100 L ₀ не значение 20 или 50, а 31,63 L ₀ . Это значение не арифметическое, а среднее геометрическое от 10 до 100, т.е. ЧАС. корень 1000 или 10 1.5 .

Расчет со степенями десяти

Есть несколько простых арифметических правил для вычислений со степенями десяти:

• Если вы умножаете натуральное число на номер шага, нули номера шага прибавляются к натуральному числу.
• Если вы умножите десятичную дробь на номер шага, десятичная точка переместится вправо на столько разрядов, сколько нулей в номере шага.
• Если вы разделите десятичную дробь на номер шага, десятичная точка переместится влево на столько разрядов, сколько нулей в номере шага.

Источник