Как вывести двоичное представление числа
Побитовые операторы и двоичное представление чисел
Язык программирования С++ обладает полным набором побитовых операторов. Побитовые операторы применяются при выполнении операций с битами в двоичном представлении числовых значений. Прежде чем непосредственно рассмотреть сами операторы, кратко остановимся на концепции двоичного представления числовых значений.
Как известно, целые числа представляются в виде последовательности цифр. Такое представление чисел называется позиционным. Весь набор цифр, которые могут использоваться в позиционном представлении числа, определяют систему счисления. В повседневной жизни используется десятичная система счисления, в которой числа представлены цифрами от 0 до 9.
В программировании более популярны системы счисления с количеством цифр, равным степени двойки: восьмеричная и шестнадцатеричная. Однако двоичная система счисления — вне конкуренции. В этой системе счисления числа записываются последовательностью из двух цифр: 0 и 1.
Каждая позиция в двоичном представлении числа соответствует биту. Таким образом, с помощью бита можно записать два значения: 0 или 1. Если для представления числа используется n бит, то в этом случае существует 2 n различных комбинаций, каждая из которых соответствует отдельному числу. Например, с помощью 8 бит(1 байт) можно записать 2 8 = 256 чисел.
При представлении двоичным кодом положительных чисел можно было бы использовать стандартное математическое представление числа в двоичной системе. Однако на практике приходится иметь дело и с отрицательными числами, причем с технической точки зрения знаком «минус» здесь не обойтись — минус можно написать на бумаге, а реализовать его в памяти компьютера намного сложнее.
Для определения знака числа используют старший бит в позиционной записи. Нулевой старший бит соответствует положительному числу, а единичный старший бит соответствует отрицательному числу. При этом перевод для положительных чисел из двоичной системы счисления в десятичную осуществляется стандартными методами: если в двоичном представлении число позиционно задается как bnbn-1. b2b1b0 (причем цифры bi могут принимать значения 0 или 1, а старший бит для положительных чисел равен 0), то в десятичной системе число вычисляется как b02 0 + b12 1 + b22 2 + . + bn-12 n-1 + bn2 n .
С отрицательными числами дела обстоят несколько сложнее. Чтобы перевести отрицательное число с позиционным представлением в двоичной системе bnbn-1. b2b1b0 (старший бит для отрицательного числа bn = 1), необходимо проделать несложную процедуру из двух этапов.
Во-первых, производится побитовое инвертирование кода, т.е. каждый бит в представлении числа меняется на противоположный: 0 на 1 и 1 на 0.
Во-вторых, результат переводится в десятичную систему и к нему добавляется 1. Это модуль отрицательного числа. Чтобы получить само число, модуль числа необходимо умножить на -1.
Чтобы перевести число из десятичной системы в двоичную, проделывают обратную процедуру: от модуля отрицательного числа отнимается 1, результат переводится в бинарный код, после чего проводится побитовое инвертирование.
Проиллюстрируем это не примере.
Рассмотрим 8-битовое бинарное положительное число 01001011, что в десятичной системе счисления соответствует числу 2 0 + 2 1 + 2 3 + 2 6 = 1 + 2 + 8 + 64 = 75.
Определим бинарное машинное представление для отрицательного числа -75. Отнимем от модуля числа единицу, получаем 74. Бинарное представление для этого числа 01001010 (74 = 2 1 + 2 3 + 2 6 ). После побитового инвертирования из числа 01001010 получаем 10110101. Это и есть представление числа -75.
В том, что это так, легко убедиться: сложим числа 01001010 и 10110101. Формально получаем 100000000, однако поскольку числа 8-битовые, лишний единичный старший бит отбрасывается, и получается представление 00000000, что соответствует нулю, как и должно быть.
Теперь рассмотрим основные побитовые операции и операторы, которые используются для этого в языке программирования С++. Список побитовых операторов приведен в таблице 1.6.
| Таблица 1.6 Побитовые операторы С++ | |
| Оператор | Назначение |
| & | |
| 5 > 5 является число -1. Дело в том, что в бинарном коде 11111010 для числа -6 при сдвиге вправо на 5 позиций при условии сохранения значения ставшего бита знака получаем код 11111111. Это код числа -1. Особенности операций в двоичной системе таковы, что сдвиг в побитовом представлении числа на одну позицию влево означает умножение этого числа на 2. Следует только помнить, что с определенного момента при сдвиге вправо теряются старшие биты. Представим, что число задается 8 битами. Если воспользоваться командной 1 6 =64. Действительно, десятичное число 1 в двоичной системе в 8-битовом представлении задается как 00000001. после сдвига влево на 6 позиций получаем 01000000, что в десятичной системе соответствует числу 64. Однако если воспользоваться командой 1 | Печать страницы | На основе Google Сайтов Источник Прямой, обратный и дополнительный коды двоичного числаПрямой код двоичного числа
Прямой код
Прямой код используется в двух вариантах.
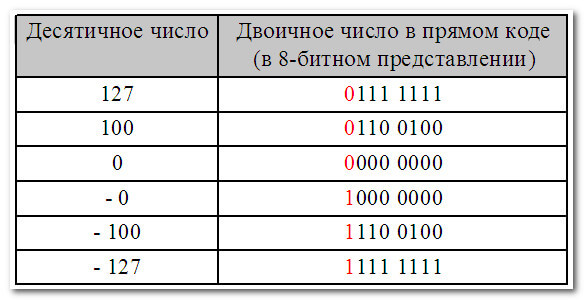
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде. При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)
Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127 Арифметические операции с отрицательными числами в обратном коде: 1-й пример (для положительного результата) 1-й этап 2-й пример (для отрицательного результата) 1-й этап 2-й этап Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки: Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит). Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.
Дополнительный код отрицательного числа можно получить двумя способами 2-й способ:
Арифметические операции с отрицательными числами в дополнительном коде Дано: необходимо сложить два числа -10 и 5 Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел. Вывод:
Источник  Что будет если не чистить кондиционер после зимы При | |
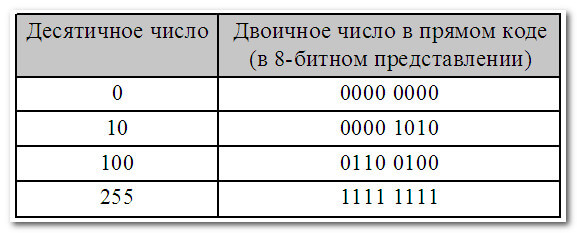В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)
Подводя итоги вопроса, не влезая в его дебри, скажу одно: 
(36 голосов, оценка: 4,67 из 5) 
