Как вывести формулу 2as

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

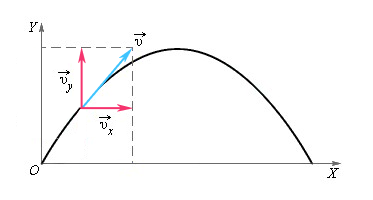
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

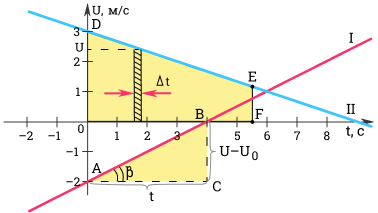
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Источник

Равноускоренное движение и ЗСИ.

Равноускоренное движение и ЗСИ.

Равноускоренное движение и ЗСИ.

Комментарий теории:#1 chichigin » 22 ноя 2014, 03:58

Равноускоренное движение
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения a остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха).
В любой точке траектории ускорение камня равно ускорению свободного падения . g
Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения.
В случае прямолинейного движения векторы скорости v и ускорения a направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.
При равноускоренном прямолинейном движении скорость тела определяется формулой
V = V₀ + at
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение.

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
Y = Y ₀ + V₀ t + at 2 /2
Это выражение называют законом равноускоренного движения.
S = V₀ t + at 2 / 2 (1)

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
S = (V 2 – V₀ 2 ) 1/2 /2a (2)

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
V = (V₀ 2 + 2aS) 1/2 (3)

Если начальная скорость υ0 равна нулю, эти формулы принимают вид
S = V 2 /2a, V = (2aS) 1/2 (4)

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0,υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

________________________________________
Импульс силы
Импульс тела
Закон сохранения импульса
________________________________________
Импульс силы.
Покой и движение тела относительны, скорость движения тела зависит от выбора системы отсчета. По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т. е. в результате взаимодействия с другими телами.
Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от v0 до до v, то ускорение a движения тела равно
a = (v – v0)/t
На основании второго закона Ньютона для силы можно написать выражение
F = ma = m(v – v1)/t. (16.1)

Из равенства (16.1) следует
Ft = mv – mv0 (16.2)
Физическая величина, равная произведению силы F на время t ее действия, называется импульсом силы.
Импульс тела.
Выражение (16.2) показывает, что имеется физическая величина, одинаково изменяющаяся у всех тел под действием одинаковых сил, если время действия силы одинаково. Эта физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела или количеством движения.
Изменение импульса тела равно импульсу силы, вызывающей это изменение. Импульс тела является количественной характеристикой поступательного движения тел. За единицу импульса в СИ принят импульс тела массой 1 кг, движущегося поступательно со скоростью 1 м/с. Единицей импульса является килограмм-метр в секунду (кг*м/с).
Закон сохранения импульса .
Выясним, как изменяются импульсы двух тел при их взаимодействии.
Обозначим скорости тел массами m ₁ и m ₂ до взаимодействия через v ₁ и v ₂ , а после взаимодействия — через v ₁ 1 и v₂ 1 .
По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить F и -F.
Для изменений импульсов тел при их взаимодействии на основании равенства (16.2) можно записать
Ft = m₁ v₁ 1 – m₁ v₁
-Ft = m₂ v₂ 1 – m₂ v₂
где t — время взаимодействия тел. Из этих выражений получаем
m₁ v₁ + m₂ v₂ = m₁ v₁ 1 + m₂ v₂ 1 (16.3)

Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.
Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равенстве нулю суммы действующих сил геометрическая сумма импульсов тел остается неизменной.
Система тел, не взаимодействующих с другими телами, не входящими в эту систему, называется замкнутой системой.
В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса.
Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.
(по материалам пособия «Физика — справочные материалы» Кабардин О.Ф.)

Далее мои, Николая Чичигина, комментарии. Как указано в статье про равноускоренное движение:

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
S = (V 2 – V₀ 2 ) 1/2 /2a (2)

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
V = (V₀ 2 + 2aS) 1/2 (3)

Если начальная скорость υ0 равна нулю, эти формулы принимают вид
S = V 2 /2a, V = (2aS) 1/2 (4)

Т.е. выражение (3), исходя из выражения (4), можно представить в виде

А отсюда следует, что при равноускоренном движении результирующая при сложении скоростей равна корню квадратному из суммы квадратов слагаемых скоростей.

Почему данный факт не учитывался при составлении ЗСИ, я уже ранее объяснял.
Почему при составлении ЗСИ нелинейную зависимость значений скоростей от перемещения заменили на линейную зависимость (не соответствующую действительности) значений скоростей от перемещения также понятно.
Почему мои «оппоненты» не желают «понять» и задуматься о правомерности ЗСИ, надеюсь, также все уже давно поняли.

Источник

Ускорение. Равноускоренное движение

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее. То есть скорость все время увеличивается.

Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, — это тоже «ускоренное» движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением .

Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 5 5 5 км/ч, потом 1 0 10 1 0 км/ч, потом 1 5 15 1 5 км/ч, 2 0 20 2 0 км/ч, 2 5 25 2 5 км/ч, 3 0 30 3 0 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1 0 10 1 0 км/ч, потом 5 5 5 км/ч, а потом 0 0 0 км/ч. То есть скорость все время уменьшается на 5 5 5 км/ч.

Следуя этой логике, через мгновение после скорости в 0 0 0 км/ч скорость должна вновь уменьшиться на 5 5 5 км/ч, и тогда скорость будет равна − 5 -5 − 5 км/ч, а потом еще уменьшиться на 5 5 5 км/ч и стать уже − 1 0 -10 − 1 0 км/ч, а потом и − 1 5 -15 − 1 5 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о «стрелочке»), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы » Два вида физических величин: скалярные величины и векторные величины » и » Проектирование векторов на оси «. В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.

Ускорение

Я думаю, что вы согласитесь с тем, что разгоняться можно по-разному: можно потихонечку, а можно — резко и очень быстро. Вроде бы в обоих этих случаях движение ускоренное, но все же разное. Надо как-то различать эти два движения. Нужна численная характеристика (характеристика числом), чтобы можно было сказать, что первое движение — медленно ускоряющееся, а второе — быстро. Такая характеристика — это ускорение: a ⃗ = V ⃗ − V 0 ⃗ t , \vec=\frac<\vec-\vec> <,>a ⃗ = t V ⃗ − V 0 ​ ⃗ ​ ​ , где V 0 ⃗ \vec V 0 ​ ⃗ ​ — начальная скорость, V ⃗ \vec V ⃗ — конечная скорость, а t t t — время, за которое скорость изменилась со своего начального значения до конечного.

Когда говорят про равноускоренное движение, то имеют в виду, что движение происходит с ускорением, которое никогда не меняется. Равное ускорение = равноускоренное движение .

— это очень полезная для нас формула. Ее нужно запомнить.

Источник