Как вывести формулу давления жидкости

Расчет давления жидкости на дно и стенки сосуда

Содержание

Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?

Взгляните на рисунок 1.

Рисунок 1. Три разных сосуда с жидкостью.

Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться.

Расчет давления жидкости на дно и стенки сосуда

Для начала рассмотрим задачу для сосуда в форме прямоугольного параллелепипеда (рисунок 2).

Рисунок 2. Определение давления жидкости на дно прямоугольного параллелепипеда.

Давление жидкости p рассчитывается по формуле: $p=FS$, где $F$ – это сила, действующая на дно сосуда, а $S$ – это площадь дна сосуда.

1. Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде.
2. Как узнать вес жидкости? Необходимо знать массу $m$ жидкости.
3. Массу $m$ мы можем вычислить по известной нам формуле:

1. Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда – $S$. Тогда объем можно вычислить по формуле:

1. Итак, подставляем наши данные в формулу для вычисления массы и получаем:

1. Таким образом, возвращаемся к весу жидкости и получаем, что:

С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, поэтому, если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:

Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($\frac<кг><м^3>$), $g=9,8 \frac<кг>$, высоту столба жидкости – в метрах (м), тогда давление $p$ будет выражено в паскалях (Па).

Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать?

1. Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба (обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине).

2. По этой формуле можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.

Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба

Примеры применения и задача

Как вы думаете, изменится ли давление на дно цилиндрического сосуда, частично заполненного водой, если в него опустить деревянный брусок?

В данном случае, уровень воды поднимется, и высота столба станет больше, значит и давление увеличится.

Какая вода: пресная или соленая оказывает большее давление на дно сосуда при одинаковом объеме?

Здесь достаточно вспомнить, что в соленой воде нам намного проще плавать и держаться на поверхности, что о говорит о ее большей плотности. Соответственно, большее давление оказывает соленая вода.

Задача. Определите давление керосина на дно цистерны, если высота столба керосина $8 м$, а его плотность $800 кг/м^3$.

Источник

Расчёт давления жидкости на дно и стенки сосуда

Тип урока: Урок открытия и первичного закрепления знаний.

Цель урока: получить выражение для расчёта давления жидкости на дно и стенки сосуда; проверка качества знаний учащихся при решении задач.

Задачи урока:

• Предметные: углубить и закрепить знания о давлении жидкости.
• Метапредметные: продолжить развивать внимание, память, логическое мышление, умение делать выводы.
• Личностные: способствовать формированию научного мировоззрения, активизировать учебно-познавательную деятельность учащихся, содействовать формированию самостоятельности, воспитанию интереса к предмету.

Оборудование к уроку: компьютер, видеопроектор, интерактивная доска, два стакана с водой, цилиндрические сосуды с основаниями различной площади, деревянный брусок, камень, два одинаковые пластмассовые груза, широкий сосуд, аквариум, удочка, каточки с заданиями, учебник по физике.

Ход урока

1.Организационный момент.

2. Актуализация имеющихся знаний.

Взаимопроверка в парах по вопросам. Слайд 1

1. Чем отличается процесс передачи давления в жидкости и газе от передачи давления твёрдыми телами? (давление твёрдыми телами передаётся в направлении действия силы, в жидкости и газе по всем направлениям одинаково)
2. Сформулируйте закон Паскаля. (давление, производимое на жидкость или газ, передаётся в любую точку без изменений во всех направлениях)
3. Мальчик выдувает мыльные пузыри. Почему они принимают форму шара? (они приобретают форму шара, так как давление в газе, согласно закону Паскаля передаётся одинаково по всем направлениям)
4. От чего зависит давление газа? (от объёма, массы и температуры газа)
5. Для космонавтов пищу изготавливают в полужидком виде и помещают в тюбики с эластичными стенками. Что помогает космонавтам выдавливать пищу из тюбиков? (Закон Паскаля)
6. Почему взрыв снаряда под водой губителен для живущих в воде организмов? (давление взрыва в жидкости, согласно закону Паскаля, передаётся одинаково по всем направлениям, и от этого животные могут погибнуть)
7. Почему пловец, нырнувший на большую глубину, испытывает боль в ушах? (с глубиной давление увеличивается; пловец испытывает боль в ушах, так как вода с большой силой давит на барабанные перепонки)

3. Открытие нового знания. Слайд 2

В три сосуда с одинаковой площадью дна, стоящие на столе, налили воды до одного уровня

1) В каком сосуде масса воды больше? Меньше?

2) Одинаковым ли будет давление воды на дно сосудов?

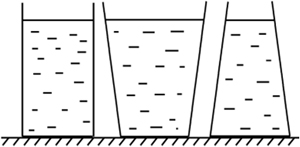
Вы уверены? Как рассчитать давление жидкости на дно сосуда? (Затруднение).

• Какая цель нашего урока? (Узнать, как рассчитать давление жидкости на дно сосуда)
• Какая тема урока? (Расчёт давления жидкости на дно и стенки сосуда) Слайд 3

Учащиеся записывают тему к себе в тетрадь.

Попытаемся вывести формулу для расчёта этого давления. Но какую же форму сосуда нам надо выбрать для расчёта нашей формулы? Я предлагаю взять форму прямоугольного параллелепипеда.

Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 2).

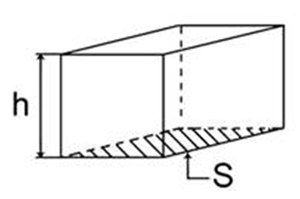
Рис. 2. Сосуд для расчета давления жидкости

Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен

жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу,

действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде

p =	P
	S

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m.

Напомним, что символом g обозначено ускорение свободного падения.

Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V

Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда

Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:

p =	ρShg
	S

В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:

p = ρgh

Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.

Полученная выше формула называется формулой гидростатического давления. Согласно этой формуле гидростатическое давление не зависит от формы сосуда, в котором находится жидкость и от площади его сечения. Оно зависит от высоты столба жидкости и от плотности жидкости.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов? (одинаковым)

Данная формула позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов?

4. Физминутка (под медленную, спокойную мелодию)

— Я предлагаю вам, ребята, выполнить дыхательную гимнастику:

1-е упр. Набрать воздух в лёгкие (вдыхаем медленно, но как можно больше воздуха),

2-е упр. Руки медленно поднимаем вверх и делаем (одновременно) глубокий вдох.

Руки опускаем – выдох.

3-е упр. Глубоко вдохнуть, садясь за парту, медленно выдыхаем (гимнастика проводится под спокойную музыку).

— Сейчас вы выполнили дыхательную гимнастику, которую врачи рекомендуют проводить 3-4 раза в день.

— А какой физический закон лежит в основе дыхательной гимнастики, как он называется? (в основе дыхательной гимнастики лежит закон Паскаля)

5. Закрепление материала.

а) Проведение игры «рыбалка»

1. Куда бы вы перелили сок из литровой банки, чтобы его давление на дно сосуда стало больше: в пятилитровую кастрюлю или в литровую бутылку? (в литровую бутылку)
2. Какие из жидкостей: вода или керосин оказывает меньшее давление на дно сосудов одной формы, если объёмы жидкостей одинаковы? (керосин)
3. Как изменится давление воды на дно доверху наполненного стакана, если в воду опустить камень? (не изменится)
4. В цилиндрический сосуд, частично наполненный водой, опустили деревянный брусок. Как изменится давление воды на дно сосуда? (увечится)
5. Два одинаковых предмета были опущены в цилиндрические сосуды с основаниями различной площади. В цилиндрических сосудах уровень воды до погружения предмета одинаков. В каком сосуде гидростатическое давление больше? (в сосуде меньшей площади)

Ответы на задачи подтверждаются опытами.

б) Расчётные задачи:

1. упр. 17(2)
2. Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8 кПа. Слайд 4

Самостоятельная работа по решению задачи упр.17(1) по рядам?

6. Подведение итогов урока. Рефлексия.

Подведём итоги.

Давайте вспомним, что сегодня делали на уроке, что узнали?

Мне очень важно, с каким настроением вы уходите с урока. Поэтому я прошу вас заполнить лист самоанализа, который находится столах у каждого из вас.

Источник

Статика. Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление).

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то дав­ление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидроста­тическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h (в окрестности точки A на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления p в основании этого столба на площадь его сечения S:

2) как вес того же столба жидкости, т. е. произведение массы m жидкости на ускорение сво­бодного падения:

Масса жидкости может быть выражена через ее плотность p и объем V:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу (1.28) значение массы из (1.29) и объема из (1.30), получим:

Приравнивая выражения (1.27) и (1.31) для силы давления, получим:

Разделив обе части последнего равенства на площадь S, найдем давление жидкости на глубине h:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободно­го падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе, давление на стенки сосуда, а так­же давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

Гидростатический парадокс .

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужа­ющихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: p = pgh (формула гидростатического давления жидкости). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосу­дов, одна и та же. Она равна весу вертикального столба ABCD жидкости: P = oghS, здесь S — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способ­ностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное дав­ление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давле­ние. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, подняв­шись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давле­ние в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Источник