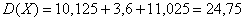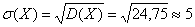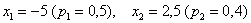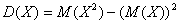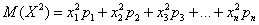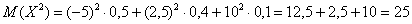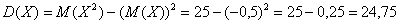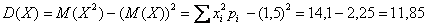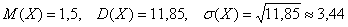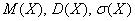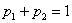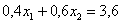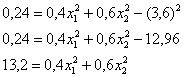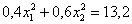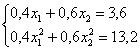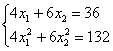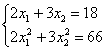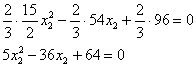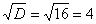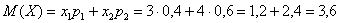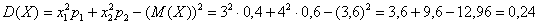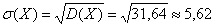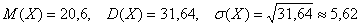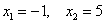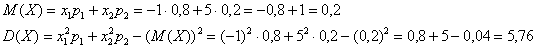Как вывести формулу дисперсии

Как найти дисперсию?

Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $\sigma(X)=\sqrt$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле: $$ D(X)=M(X-M(X))^2, $$ которую также часто записывают в более удобном для расчетов виде: $$ D(X)=M(X^2)-(M(X))^2. $$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид: $$ D(X)=\sum_^-\left(\sum_^ \right)^2. $$ Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx — \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения: $$ x_i \quad 1 \quad 2 \\ p_i \quad 0.5 \quad 0.5 $$ и $$ y_i \quad -10 \quad 10 \\ p_i \quad 0.5 \quad 0.5 $$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии: $$ D(X)=\sum_^-\left(\sum_^ \right)^2 =\\ = 1^2\cdot 0.5 + 2^2 \cdot 0.5 — (1\cdot 0.5 + 2\cdot 0.5)^2=2.5-1.5^2=0.25. $$ $$ D(Y)=\sum_^-\left(\sum_^ \right)^2 =\\ = (-10)^2\cdot 0.5 + 10^2 \cdot 0.5 — (-10\cdot 0.5 + 10\cdot 0.5)^2=100-0^2=100. $$ Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $\sigma(X)=0.5$, $\sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения: $$ x_i \quad -1 \quad 2 \quad 5 \quad 10 \quad 20 \\ p_i \quad 0.1 \quad 0.2 \quad 0.3 \quad 0.3 \quad 0.1 $$

Снова используем формулу для дисперсии дискретной случайной величины: $$ D(X)=M(X^2)-(M(X))^2. $$ В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание: $$ M(X)=\sum_^ =-1\cdot 0.1 + 2 \cdot 0.2 +5\cdot 0.3 +10\cdot 0.3+20\cdot 0.1=6.8. $$ Потом математическое ожидание квадрата случайной величины: $$ M(X^2)=\sum_^ = (-1)^2\cdot 0.1 + 2^2 \cdot 0.2 +5^2\cdot 0.3 +10^2\cdot 0.3+20^2\cdot 0.1=78.4. $$ А потом подставим все в формулу для дисперсии: $$ D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16. $$ Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x \in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx — \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$ Вычислим сначала математическое ожидание: $$ M(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x dx = \int_<0>^ <6>\frac <18>\cdot x dx = \int_<0>^ <6>\frac <18>dx = \left.\frac <54>\right|_0^6=\frac<6^3> <54>= 4. $$ Теперь вычислим $$ M(X^2)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx = \int_<0>^ <6>\frac <18>\cdot x^2 dx = \int_<0>^ <6>\frac <18>dx = \left.\frac <72>\right|_0^6=\frac<6^4> <72>= 18. $$ Подставляем: $$ D(X)=M(X^2)-(M(X))^2=18-4^2=2. $$ Дисперсия равна 2.

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку «Вычислить».
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Дисперсия дискретной случайной величины.
Среднее квадратическое отклонение

Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:

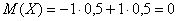
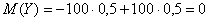
«Снайперское» математическое ожидание равно , однако и у «интересной личности»: – оно тоже нулевое!

Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.

Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:

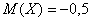
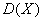
Там мы нашли неутешительное математическое ожидание этой игры, и сейчас нам предстоит вычислить её дисперсию, которая обозначается через .

Выясним, насколько далеко «разбросаны» выигрыши/проигрыши относительно среднего значения. Очевидно, что для этого нужно вычислить разности между значениями случайной величины и её математическим ожиданием:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

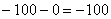
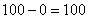
Теперь вроде бы нужно просуммировать результаты, но этот путь не годится – по той причине, что колебания влево будут взаимоуничтожаться с колебаниями вправо. Так, например, у стрелка-«любителя» (пример выше) разности составят , и при сложении дадут ноль, поэтому никакой оценки рассеяния его стрельбы мы не получим.

Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей: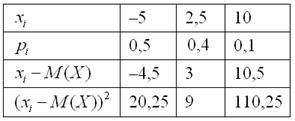

И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:

– определение дисперсии. Из определения сразу понятно, что дисперсия не может быть отрицательной – возьмите на заметку для практики!

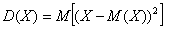
Вспоминаем, как находить матожидание. Перемножаем квадраты разностей на соответствующие вероятности (продолжение таблицы):
– образно говоря, это «сила тяги»,
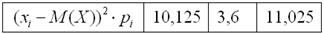
и суммируем результаты:

Не кажется ли вам, что на фоне выигрышей 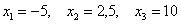результат получился великоватым? Всё верно – мы возводили в квадрат, и чтобы вернуться в размерность нашей игры, нужно извлечь квадратный корень. Данная величина называется средним квадратическим отклонением и обозначается греческой буквой «сигма»:

Иногда это значение называют стандартным отклонением.

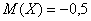
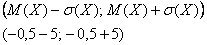
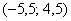
В чём его смысл? Если мы отклонимся от математического ожидания влево и вправо на среднее квадратическое отклонение:

– то на этом интервале будут «сконцентрированы» наиболее вероятные значения случайной величины. Что мы, собственно, и наблюдаем:

Однако так сложилось, что при анализе рассеяния почти всегда оперируют понятием дисперсии. Давайте разберёмся, что она означает применительно к играм. Если в случае со стрелками речь идёт о «кучности» попаданий относительно центра мишени, то здесь дисперсия характеризует две вещи:

Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим 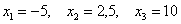в 10 раз, то математическое ожидание увеличится в 10 раз, а дисперсия – в 100 раз (коль скоро, это квадратичная величина). Но, заметьте, что сами-то правила игры не изменились! Изменились лишь ставки, грубо говоря, раньше мы ставили 10 рублей, теперь 100.

Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:

Игра с низкой дисперсией – это осторожная игра. Игрок склонен выбирать самые надёжные схемы, и в ситуации неопределённости не ставит слишком большие деньги. Например, система «красное/чёрное» в рулетке (см. Пример 4 статьи Случайные величины).

Игра с высокой дисперсией. Её часто называют дисперсионной игрой. Это авантюрный или агрессивный стиль игры, где игрок выбирает «адреналиновые» схемы. Вспомним хотя бы «Мартингейл», в котором на кону оказываются суммы, на порядки превосходящие «тихую» игру предыдущего пункта.

Показательна ситуация в покере: здесь есть так называемые тайтовые игроки, которые склонны осторожничать и «трястись» над своими игровыми средствами (банкроллом). Неудивительно, что их банкролл не подвергается значительным колебаниям (низкая дисперсия). Наоборот, если у игрока высокая дисперсия, то это агрессор. Он часто рискует, делает крупные ставки и может, как сорвать огромный банк, так и програться в пух и прах .

То же самое происходит на Форексе, других биржах и так далее – примеров масса.

Причём, во всех случаях не важно – на копейки ли идёт игра или на тысячи долларов. На любом уровне есть свои низко- и высокодисперсионные игроки. Ну а за средний выигрыш, как мы помним, «отвечает» математическое ожидание.

Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:

Формула для нахождения дисперсии

Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой: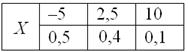

и найденное матожидание .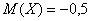

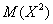
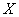
Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание – квадрата случайной величины . По определению математического ожидания:

В данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

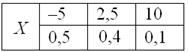
Дискретная случайная величина задана своим законом распределения:

Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в дурдоме с определёнными вероятностями 🙂

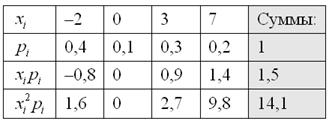
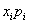
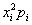
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем и, наконец, суммы в правом столбце:

Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .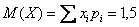

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
– лично я обычно округляю до 2 знаков после запятой.

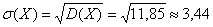
Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:

вот здесь уже трудно ошибиться 🙂

Ответ:

Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!

Пара заданий для самостоятельного решения:

Вычислить дисперсию случайной величины 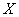предыдущего примера по определению.

И аналогичный пример:

Дискретная случайная величина задана своим законом распределения:

Найти

Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.

Решения и ответы внизу страницы.

В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

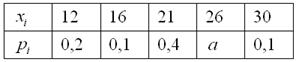
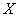
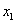
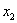
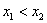
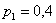
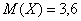
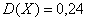
Дискретная случайная величина может принимать только два значения: и , причём . Известна вероятность , математическое ожидание и дисперсия .

Найти .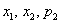

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

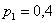
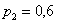
и поскольку , то .

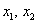
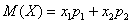
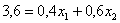
Осталось найти …, легко сказать 🙂 Но да ладно, понеслось. По определению математического ожидания:
– подставляем известные величины:

– и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
– подставляем известные данные:

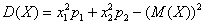
или:

О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:

и делим на 2:

Вот так-то лучше. Из 1-го уравнения выражаем:
(это более простой путь) – подставляем во 2-е уравнение:

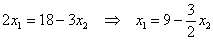
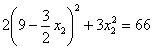
Возводим в квадрат и проводим упрощения: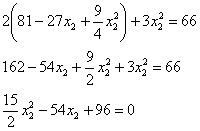

Умножаем на :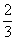

В результате получено квадратное уравнение, находим его дискриминант:
– отлично!

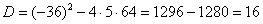
и у нас получается два решения:

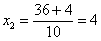
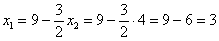
1) если , то ;

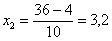
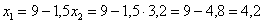
2) если , то .

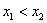
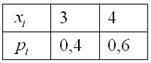
Условию удовлетворяет первая пара значений. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

и выполним проверку, а именно, найдём матожидание:

и дисперсию:

В результате получены исходные значения, что и требовалось проверить.

Ответ:

Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:

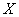
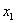
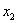
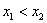
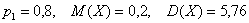
Случайная величина принимает только два значения: и , причём . Найти эти значения, если .

Тут вычисления попроще.

Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!

Решения и ответы:

Пример 7. Решение: вычислим математическое ожидание: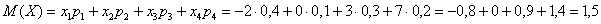

Вычислим дисперсию по определению: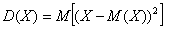
Заполним расчётную таблицу: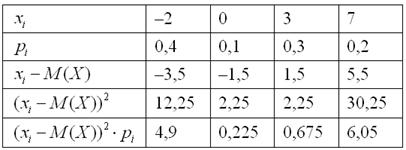

Таким образом:

Ответ:

Пример 8. Решение: случайная величина может принять только 5 значений, поэтому: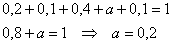

Заполним расчётную таблицу: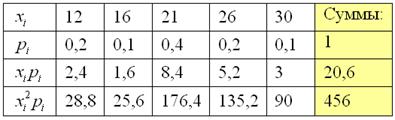

Математическое ожидание: .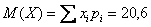
Дисперсию вычислим по формуле: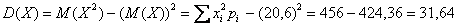

Среднее квадратическое отклонение:

Ответ:

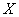
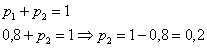
Пример 10. Решение: т.к. случайная величина может принимать только 2 значения, то:
.
По определению математического ожидания: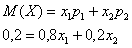

По формуле вычисления дисперсии: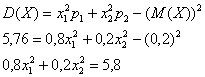

Составим и решим систему: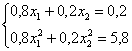

Умножим оба уравнения на 5: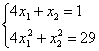

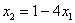
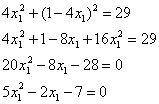
Из первого уравнения выразим: – подставим во второе:

Решим полученное квадратное уравнение: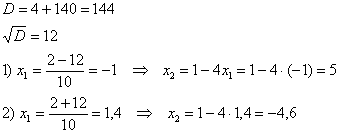

Условию 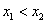удовлетворяет первая пара.

Ответ:

Проверка:

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник