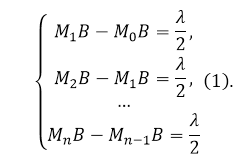Как вывести формулу для радиуса зоны френеля

Зоны Френеля

Зона Френеля — это цилиндрический эллипс, проведенный между передатчиком и приемником. Размер эллипса определяется частотой работы и расстоянием между двумя участками. Когда радиосигнал проходит между передатчиком и приемником, он может распространяться несколькими путями. Он может идти напрямую между передатчиком и приемником (основной сигнал). Сигнал может отражаться от земли и затем переноситься на удаленный приемник (отраженный сигнал). Он может идти влево или вправо и отражаться от «холма» (еще один отраженный сигнал).

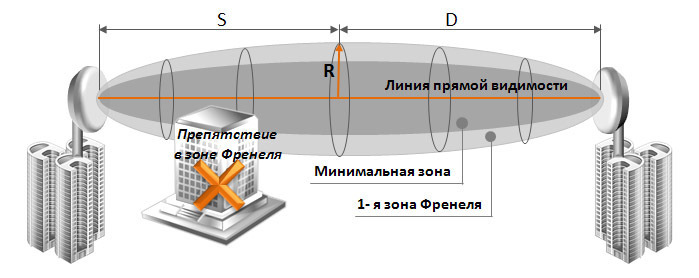
Другими словами, радиоволна в процессе распространения движется не только по прямой траектории и не в виде «луча» (хотя лучевые модели распространения радиоволн и применяются в расчете различных задач технической электродинамики). Когда волна перемещается на значительные расстояния, измеряемые сотнями длин волн, она, в результате распространения, занимает некий объем в форме эллипса:

По сути, внутри этого эллипса располагается вся полезная энергия и передаваемая информация. Для того, чтобы сигнал мог быть эффективно передан, должны соблюдаться два условия:

• обеспечена прямая видимость между передатчиком и приемником;
• не менее 60% занимаемого эллипса должно быть свободно от препятствий.

Понятно, что при отсутствии прямой видимости качественная связь на больших расстояниях затруднительна. Но с требованиями к отсутствию препятствий в зоне Френеля все не так однозначно. Наличие препятствий внутри эллипсоида распространения радиоволн может приводить к наводкам, помехам или просто вносить дополнительное затухание (как, например, в случае с лесным массивом).

Если устанавливать радиомост только из условия наличия прямой видимости, то, вероятнее всего, на детекторе качества сигнала вы увидите значение 95-98%. Но при этом скорость передачи данных может оказаться минимальной (из-за потерь и повтора пакетов) по причине наличия препятствий внутри зоны Френеля.

Для расчета радиуса зоны Френеля можно воспользоваться упрощенной, но подтвержденной на практике формулой:

где R – радиус зоны Френеля (м);
S,D – расстояние от антенн до самой высокой точки предполагаемого препятствия (км);
f – частота (ГГц).

Когда радиус зоны Френеля над предполагаемым препятствием рассчитан, нужно понять не занимает ли препятствие больше 40% рассчитанного радиуса:

Что же делать в том случае, если препятствие закрывает большую часть радиуса этого эллипса и свободным от препятствий остается менее 60% зоны Френеля? В этом случае задача организации стабильного радиосигнала решается только путем поднятия антенн на соответствующую высоту, чтобы в месте наличия препятствия зона Френеля была достаточно свободна. После подъема антенн на необходимую высоту на обеих сторонах, линк будет работать на максимальной скорости и с максимальной для данного расстояния отдачей.

Еще следует отметить, что мы живем в трехмерном пространстве (amazing!). Поэтому следует учитывать и препятствия, которые находятся сбоку. Например, в случае построения линка, луч которого проходит между двух зданий, должно соблюдаться то же самое условие:

Таким образом, зона Френеля и, как следствие, размер эллипса определяется частотой работы и расстоянием между двумя конечными точками радиомоста (передатчиком и приемником). При этом отметим, что зона Френеля состоит из нескольких зон, причем зона 1 имеет самый сильный сигнал, а следующие зоны (зона 2 и зона 3) имеют более слабые сигналы:

Исходя из рисунка выше, зона Френеля рассчитывается с использованием следующего уравнения:

Зона Френеля — это область вокруг линии прямой видимости, вдоль которой распространяются радиоволны после того, как покидают антенну. Для организации стабильного радиоканала вам потребуется четкая линия видимости для обеспечения хорошего уровня сигнала. Это необходимое условие, но не достаточное. Важно знать в каком состоянии находится зона Френеля. Как правило, блокировка 20% зоны Френеля приведет к наличию небольших потерь сигнала в канале. В том случае, если препятствие закрывает 40% зоны Френеля, то потеря сигнала станет значительной.

Вот еще упрощенная формула для определения радиуса самой широкой точки зоны Френеля (в метрах):

где d — расстояние (в километрах) между двумя антеннами, а f — частота (в ГГц), на которой вы осуществляете передачу.

При расчета высоты установки антенн рекомендуем пользоваться следующим онлайн-расчетчиком: Ubiquiti Outdoor Wireless Link Calculator.

Источник

Зона Френеля

Что такое зона Френеля

Зонами Френеля называют области, на которые можно разделить поверхность световой, либо звуковой волны с целью расчета результатов дифракции света или звука.

Методика анализа была впервые применена О. Френелем в 1815 – 1819 годах. Зону Френеля можно наглядно представить в виде объема радио-волнового канала между двумя передатчиками сигнала.

Максимальное значение объема канала отмечено центральной точкой, равноудаленной от двух антенн. Наиболее качественный сигнал обеспечивается путем подбора максимально чистой зоны, в которой отсутствуют физические и радио-волновые препятствия.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Расчет радиуса зоны Френеля

С помощью определенных характеристик можно выполнить корректный расчет. Для определения зоны Френеля в ее центре необходимо использовать формулу:

Где D равно расстоянию в километрах, f является частотой в GHz.

Если необходимо рассчитать размер зоны Френеля в любой ее точке, к примеру, в месте, где обнаружено препятствие, следует воспользоваться формулой:

Где f — это частота в GHz, D1 является расстоянием от первой антенны до искомой точки в километрах, D2 равно расстоянию от второй антенны до искомой точки в километрах.

Знание характеристик зоны Френеля позволяет выполнить точные расчеты. В практическом применении представленные формулировки обеспечивают данные для стабильности параметров беспроводного моста и максимально возможной скорости передачи сигнала.

Метод зон Френеля, основные принципы работы

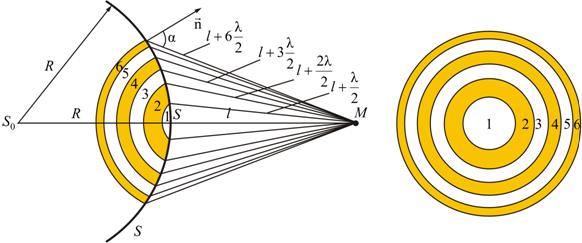
С целью упрощения решений задач волновая поверхность S разбивается на отдельные зоны. Данный способ называют методом зон Френеля.

Точки поверхности S, которые являются границей первой или центральной зоны и удалены от точки М на расстояние:

Точки сферы S, которые находятся на расстоянии:

и так далее относительно точки М, образуют 2, 3 и так далее зоны Френеля.

В точке М образуются колебания. Они расположены между двумя соседними зонами, фазы которых противоположны по причине разности ходя от этих зон до точки М:

В процессе сложения колебания друг друга ослабляют:

Где A является амплитудой результирующего колебания, Аi представляет собой амплитуду колебаний, возбуждаемую i-й зоной Френеля.

Значение Аi определяется площадью Si зоны и углом αi между нормалью к поверхности и прямой, направленной в точку M. Расчет площади одной зоны выглядит следующим образом:

Исходя из представленного уравнения, можно сделать вывод о независимости площади зоны Френеля от номера зоны i. Данное утверждение позволяет сделать вывод о том, что при малых числах i соседние зоны будут обладать одинаковыми площадями. В то время, как номер зоны увеличивается, возрастает угол αi, а также снижается интенсивность излучения зоны по направлению к точке М, то есть уменьшается амплитуда Аi. Другой причиной данного явления служит увеличение расстояния до точки М: \(x = <-b \pm \sqrt\over 2a>\) В целом количество зон Френеля, которые уменьшаются на части сферы, направленной к точке М, достаточно большое:

если радиус R=l=1 метр,

\(\lambda =-5\times 10^<-7>\) составляет 500 нм.

Количество зон \(N\approx 3\times 10^<5>\)

Радиус первой зоны \(r_<1>\approx 0.16\) мм

Исходя из вышеизложенной информации, можно сделать вывод о равенстве углов соседних зон между нормалью к зоне и направлением на точку М. Таким образом, наблюдается примерное равенство амплитуд волн, которые приходят в точку М от соседних волн. При прямолинейном распространении световой волны фазы колебаний, которые образованы в соседних зонах, будут отличаться на π. Согласно этим данным, в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны рассчитывается, как среднее арифметическое от амплитуд зон, которые к ней примыкают:

В таком случае, исходное уравнение можно преобразовать следующим образом:

Из равенства площадей, которыми обладают соседние зоны, вытекает нулевое значение выражения, заключенного в скобках. Тогда результирующая амплитуда будет равна:

Расчет интенсивности излучения имеет вид:

Таким образом, результирующая амплитуда, которая образована в какой-либо точке М всей сферической поверхностью, определяется, как половина амплитуды, сформированной одной лишь центральной областью, а интенсивность составляет:

Радиус, которым характеризуется центральная зона, небольшой:

\(r_<1>\approx 0.16\) мм

Тогда допустимо считать распространение света от точки Р до точки М прямолинейным. В условиях, когда путь волны преграждает непрозрачный экран, в котором есть отверстие, открывающее только центральную зону Френеля, то амплитуда в точке М составляет А1. Поэтому, интенсивность в точке М превышает в 4 раза тот же показатель, но в условиях без экрана. В случае, когда все зоны с четными номерами закрыты, интенсивность света будет увеличиваться.

Таким образом, объясняют прямолинейность распространения света в условиях однородной среды с помощью принципа Гюйгенса-Френеля. Справедливость деления волнового фронта на зоны Френеля нашла подтверждение в ходе эксперимента. Для опыта используют зонные пластинки, представляющие собой систему чередующихся прозрачных и непрозрачных колец. Эксперимент подтверждает возможность увеличения освещенности в точке М с помощью зонных пластинок по принципу собирающей линзы.

Принцип Гюйгенса-Френеля

Дифракцией света в наиболее распространенном понятии называют огибание световыми лучами границы непрозрачных тел или экранов, то есть проникновение света в область с геометрической тенью.

Максимально рельефно дифракцию света можно наблюдать в зонах с резким изменением плотности потока лучей:

• около каустик;
• вблизи фокуса линзы;
• у границ геометрической тени.

Дифракция волн тесно связана с процессами, при которых волны распространяются и рассеиваются в неоднородных средах.

Дифракция — это комплекс явлений, которые можно наблюдать в процессе распространения света в среде, отличающейся резкими неоднородностями, габариты которых соотносимы с длиной волны и связаны с отклонениями от законов геометрической оптики.

Огибание препятствий звуковыми волнами, то есть дифракцию звуковых волн, можно заметить в повседневной жизни.

К примеру, за углом дома слышен звук. Для того чтобы наблюдать дифракцию световых лучей, требуются специальные условия, что является причиной небольшой длины световых волн. Интерференция не отличается существенно от дифракции. Данные явления зависят от перераспределения светового потока в результате суперпозиции волн.

Дифракция объясняется принципом Гюйгенса. Согласно данному утверждению, каждая точка, которую достигает волна, является центром вторичных волн, а огибающая этих волн определяет положение волнового фронта в следующий момент времени.

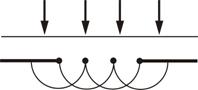
На рисунке изображен непрозрачный экран, на отверстие в котором нормально падает плоская волна.

Каждая точка области волнового фронта, выделенного отверстием, представляет собой источник вторичных волн. В условиях однородной среды они будут иметь сферическую форму. С помощью огибающих вторичных волн для некоторого момента времени можно увидеть, что фронт волны достигает области геометрической тени, то есть волна огибает края отверстия.

Благодаря принципу Гюйгенса, можно решить задачу, связанную с направлением, в котором распространяется волновой фронт. Но утверждение не касается вопроса о таких характеристиках разнонаправленных волн, как амплитуда и интенсивность. Решающая роль в определении волновой природы света отведена О. Френелю, который проводил данные исследования в начале XIX века. Ученый представил объяснение явлению дифракции и ее количественный расчет. В 1818 году Френель был удостоен премии Парижской академии за достижения в данной области.

Френель дополнил принцип Гюйгенса физическим смыслом с помощью идеи интерференции вторичных волн. Ученый рассматривал дифракцию по средствам нескольких ключевых положений, которые не требую доказательств. Комплекс данных утверждений называют принципом Гюйгенса-Френеля. Исходя из принципа Гюйгенса, каждая точка фронта волны рассматривается в качестве источника вторичных волн. Френель значительно развил это утверждение:

1. Все вторичные источники фронта волны, которая исходит из одного источника, когерентны между собой.
2. Участки волновой поверхности с разными площадями испускают равные интенсивности или мощности.
3. Для каждого вторичного источника характерно излучение света в большей степени по направлению к внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при \(\alpha \geq \frac<\pi ><2>\)
4. Вторичные источники характеризуются принципом суперпозиции, то есть излучение одних областей волновой поверхности не оказывает влияние на излучение других участков. Это можно понять, когда часть волновой поверхности прикрыта непрозрачным экраном, а вторичные волны излучаются открытыми областями так, как если бы экран отсутствовал.

Благодаря данным положениям, Френелю удалось составить дифракционную картину. Используя справедливые утверждения, ученый выполнял количественные расчеты, характеризующие явление дифракции.

Источник

Зоны Френеля

Вы будете перенаправлены на Автор24

Вычисление амплитуды световых колебаний с использованием аналитического выражения принципа Гюйгенса — Френеля является в общем случае сложной, нетривиальной задачей. Однако Френель показал, что в некоторых случаях при наличии симметрии найти амплитуду суммарных колебаний можно используя алгебраическое или геометрическое суммирование.

Пусть сферическая или плоская волна попадает на экран с отверстием. Необходимо определить, как распределяется интенсивность света за экраном. Для того чтобы решить эту задачу используя принцип Гюйгенса — Френеля делают предположения:

Непрозрачные части экрана не работают как источники вторичных волн.

В отверстии экрана точки волнового фронта служат источником вторичных волн, как будто нет экрана.

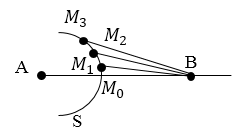
Пусть точка А является источником сферической волны, $S$ — волновой фронт в момент времени $t$.

Для того чтобы найти интенсивность волны в точке $В$, надо разбить поверхность $М$ на зоны — кольца, имеющие такие размеры, чтобы расстояния от краев зоны до точки $В$ были различны на величину $\frac<\lambda ><2>$. Границы зон на рис.1 обозначены как $M_0,\ M_1,\ M_2,\dots $ Запишем вышеназванное условие как:

Центральная зона носит название нулевой ($M_0$). Иногда центральную зону называют первой, при этом говорят, что $m=1,2,$ .

Готовые работы на аналогичную тему

Радиусы и площади зон Френеля

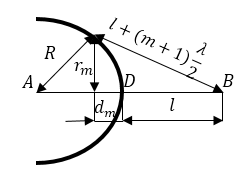
Для определения радиусов зон рассмотрим рисунок (рис. 2). На этом рисунке: радиусы зон $r_1,\ r_2,\dots ,r_m.$ $R$ — радиус кривизны сферического фронта волны. Точка $D$ обозначает место пересечения фронта волны с прямой $АВ$, $d_1,\ d_2,\dots ,d_m-$ расстояния от точки $D$ до проекции границы соответствующей зоны на прямую $АВ$. Из рис.2 видно, что для радиуса $r_m$ будет справедливо уравнение:

Если ограничиться точностью величин до $<\lambda >^2$ из уравнения (2) следует:

Используя второе выражение из (3) площадь нулевой зоны найдем как:

Найдем суммарную площадь первой и нулевой зон, получим:

Соответственно площадь первой зоны равна:

Получилось, что площадь первой зоны равна площади нулевой зоны. Выражение (6) определяет площади и всех остальных зон. Пренебрегая кривизной поверхности фронта волны считают, что площадь кольцевой зоны на поверхности волнового фронта равна ее проекции на плоскость, которая перпендикулярна прямой $АВ$. Если радиусы зон Френеля существенно меньше радиуса кривизны волнового фронта, то ошибка в таком допущении небольшая. Если длины волн малы, из формулы (3) можно сделать вывод, что данное условие хорошо выполнимо для большого количества зон Френеля.

Амплитуды колебаний

Амплитуды колебаний, которые возбуждаются в точке В зонами Френеля образуют монотонно убывающую последовательность. При этом фазы колебаний, которые возбуждают соседние зоны отличны на $\pi $. Поэтому амплитуда результирующего колебания в точке В может быть записана как:

Запишем выражение (7) в ином виде:

Так как амплитуда ($A_m$) монотонно убывает, то приближенно можно положить, что:

В таком случае выражение (8) преобразуется до:

В соответствии с выражением (10) амплитуда волны в точке $В$ равна половине амплитуды волны, которая создается центральной зоной.

Задание: Длина волны, которую посылает точечный источник света, равна $\lambda=500нм$. Источник находится на расстоянии $a=1м$ от непроницаемого для света экрана с круглым отверстием диаметр его, равен $d=1\ мм$. Каким должно быть расстояние от экрана до точки, в которой ведутся наблюдения ($b$), если отверстие открывает три зоны Френеля?

Решение:

Будем считать, что центральная зона — первая, то есть $m=1,2,3$ .

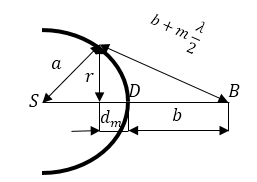
Исходя из рис.4, можно записать:

Из численных данных задачи имеем, что:

\[\lambda \ll a,\ \to \lambda \ll b\left(1.2\right).\]

Преобразуем выражение (1.1) к виду:

Выразим $d_m$, и $r^2$, учитывая, что выражение $\frac<4<(a+b)>^2>m^2<\lambda >^2$мало, и им можно пренебречь, получим:

Используя условие: $r=\frac<2>$, из формулы для $r^2$ (1.4) найдем расстояние $b$:

Проведем вычисления, получим:

Ответ: $0,2 м$.

Задание: Каким будет число зон Френеля, которые откроет отверстие радиусом r, если поле исследуется на расстоянии b от центра отверстия. Считать падающую волну плоской.

Решение:

Исходя из выражения, которое определяет зоны Френеля:

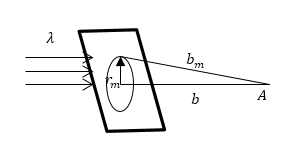
используя формулу для радиусов зон (рис.5):

Так как длина волны видимого света мала, то ее квадратами можно пренебречь, то есть получаем:

Если по условию задачи радиус отверстия равен r, то искомая величина:

Источник