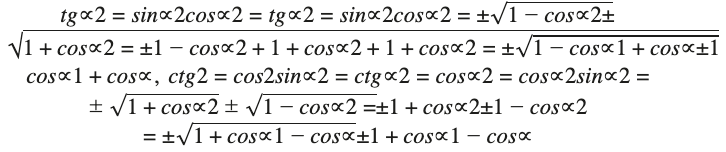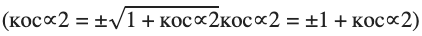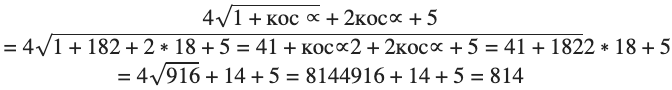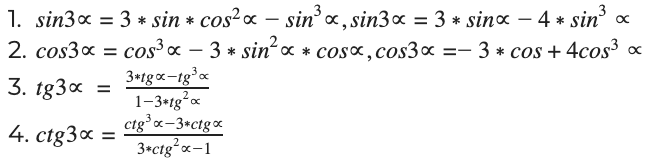Как вывести формулу косинуса тройного угла

Половинный и тройной аргумент тригонометрической функции: формулы

Содержание:

Синус, косинус, тангенс, котангенс – отношения между выражениями в тригонометрии. Для каждого из них предусмотрена отдельная методика, которая используется при расчете значения. Все функции плотно связаны между собой. Это обуславливает большое количество математических структур. Основные из них обеспечивают:

• Связь функционалов одинаковых углов;
• Взаимозависимость кратных углов;
• Возможность снизить степень. Это достигается за счет вынесения переменной или группы переменных, других действий;
• Выражение одного функционала через другие доступные функции: двойной, тройной, половинный аргумент тригонометрия применяет для решения ряда заданий.

Формулы половинного аргумента – тригонометрия

Формула половинного аргумента – косинуса или других примеров тригонометрии – это противоположенная конструкциям двойных углов методика. Она основана на использовании угла α для выражения \frac <\alpha> <2>. Все тригонометрические конструкции половинных углов выходят из формул двойного угла.

Выражения для двойных аргументов позволяют выразить значения sinsin2α, coscos2α, tg2α, ctg2α с помощью cossinsinα, tgα, ctgα. В качестве аргумента могут выступать не только углы, но и цельные выражения. Существуют легкий и сложный тип примеров. Общий вид конструкции для расчета половинных аргументов:

Формула половинного аргумента синуса и косинуса

Для выведения уравнения косинусов и синусов половинных углов используется косинус двойных углов:

Для этого необходимо записать их в следующей форме: cos = 1-2 sinα2cosα = 1-2 Sin2α2 cosα=2
Кос2α2-1cosα=2 кос2α2-1

Первое равенство sinα2sinα2 позволяет предположить: \sin \alpha 2 = \pm \sqrt

По аналогии решается второй пример: cosα2cosα2
Косα2 = \pm \sqrt

Формулы половинного аргумента тангенса и котангенса

Для выведения выражений тангенса половинных углов используется стандартная функция: tgα2 = sinα2cosα2tgα2 = sinα2cosα2. Чтобы вывести котангенс, понадобится ctgα2 = cosα2sinα2ctgα2 = cosα2sinα2. Рекомендуется использовать также выражения синуса, косинуса, доказанные ранее.

Формулы половинного аргумента тригонометрических функций: примеры задач

Рассмотрим примеры задач:

1. Необходимо решить пример:

4 кос∝2 + 2 кос∝ + 54 кос∝2 + 5

кос∝ = 18 кос∝ = 18

Для решения задачи используется следующее выражение:

Необходимо упростить пример, для этого действуем:

В итоге получаем: 4 кос∝2 + 2 кос∝ + 5 = 8144 кос∝2 + 2 кос∝ + 5 = 814

2. Необходимо найти решение

кос30°= \sqrt 3 *2кос30°=32

Следует рассчитать половинный угол для тригонометрического функционала косинуса. Для этого:

кос2∝2 = 1 + кос∝2кос2∝2 = 1 + кос∝2

Подставляем существующие данные:

кос2 15°=1 + кос30° 2 = кос 215° = 1 + кос30° 2 = 1+ \sqrt 32 2 = \sqrt 341 + 322 = 2 + 34

В условии заданы параметры кос2 15°кос215°, необходимо вычислить кос15°кос15°.

Место расположения угла в пятнадцать градусов – первая координатная четверть, значение косинуса положительное. Отсюда следует:

кос15°= \sqrt 2 + \sqrt 3 * 4 = кос15°= 2 + 34 = \sqrt 2 + \sqrt 3 * 22 + 32

Решение: кос15°= \sqrt 2 + \sqrt 3 2 кос15° = 2 + 32

Тригонометрические формулы тройного аргумента

Все тригонометрические выражения для двойных, тройных углов называются также формулой для кратных углов. Они используются для выявления тригонометрического функционала углов двойного, тройного типа, через одинарный угол α. В основе операций – сложение. Рассмотрим основные четыре формулы:

Формула синуса тройного аргумента – доказательство

Для доказательства формулы синуса тройных углов применяется сумма и разность между ними. Рекомендуется использование формул для двойных углов. Получаем доказательство:
sin3∝ = sin 2∝ + ∝ = sin3∝ = sin 2∝ + ∝ = sin2∝cos∝ + cos2∝sin∝ = sin2∝ + cos2∝sin∝ = 2sincoscos + cos2∝ — sin2∝*sin∝ = 2sin∝cos∝ + cos2∝ — sin2sin∝ = 3sin∝cos∝ — sin3∝3sin∝cos2∝ — sin3∝

В полученном выражении проводится замена: sin3∝ = 3sin∝cos∝ -sin3∝sin3∝ = 3sin∝cos2∝ — sin3∝cos2∝cos2

Заменяем на выражение 1-sin2∝1-sin2∝

Результат: — sin3∝ = 3sin∝ — 4sin3∝sin3∝ = 3sin∝ — 4sin3∝

Косинус тройного аргумента – доказательство

Доказательство формулы косинуса тройных углов выглядит следующим образом:

cos3∝ = cos 2∝ + ∝ = cos 2∝ + ∝ = cos2∝cos∝ — sin2sin∝ = cos2∝cos∝ — sin2∝sin∝ = (cos2∝ — sin2∝) cos∝ — 2sin∝cos∝sin∝ + = (cos2∝ — sin2∝ )*cos∝ — 2sin∝cos∝sin∝ + = cos3∝ — 3sin2∝cos∝cos3∝ — 3sin2∝cos∝.

Проводится замена аргумента. Вместо 3α = cos3α − 3sin2αcosαcos 3α = cos3α — 3sin2αcosα sin2αsin2α вставляем 1 — cos2∝1 — cos2

Итоговое решение: cos3∝ = 4cos3∝ — 3cos∝cos3∝ = 4cos3∝ — 3cos∝

Источник

Формулы двойного угла в тригонометрии

Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.

Список формул двойного угла

Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .

Ниже приведены формулы двойного угла:

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α

Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .

Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.

Доказательство формул двойного угла

Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:

sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что

sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α

Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .

Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .

Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:

t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α

Примеры использования формул двойного угла

Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .

Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .

Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и

sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что

2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3

и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3

Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.

Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .

Представить sin 2 α 3 через тригонометрические функции, при α 6 .

Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6

Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .

Формулы тройного, четверного и т.д. угла

Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.

sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α

При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .

Так же приводится формула косинуса тройного угла:

cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α

При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .

При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:

t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1

Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.

Источник

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

\(\blacktriangleright\) Основные тождества: \[\begin <|l|l|>\hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm\, \alpha \cdot \mathrm\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm\, \alpha=\dfrac<\sin \alpha> <\cos \alpha>&\mathrm\, \alpha =\dfrac<\cos \alpha> <\sin \alpha>\\&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin <|l|r|>\hline &\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm\, (\alpha\pm \beta)=\dfrac<\mathrm\, \alpha\pm \mathrm\, \beta><1 \mp \mathrm\, \alpha\cdot \mathrm\, \beta> & \mathrm\, (\alpha\pm\beta)=-\dfrac<1\mp \mathrm\, \alpha\cdot \mathrm\, \beta><\mathrm\, \alpha\pm \mathrm\, \beta>\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin <|lc|cr|>\hline \sin <2\alpha>=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos<2\alpha>=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin <2\alpha>&& & \cos<2\alpha>=2\cos^2\alpha -1\\ & & & \cos<2\alpha>=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm\, 2\alpha = \dfrac<2\mathrm\, \alpha><1-\mathrm^2\, \alpha> && & \mathrm\, 2\alpha = \dfrac<\mathrm^2\, \alpha-1><2\mathrm\, \alpha>\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin <3\alpha>=3\sin \alpha -4\sin^3\alpha && & \cos<3\alpha>=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin <|lc|cr|>\hline &&&\\ \sin^2\alpha=\dfrac<1-\cos<2\alpha>>2 &&& \cos^2\alpha=\dfrac<1+\cos<2\alpha>>2\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin <|c|>\hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>-\cos<(\alpha+\beta)>\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>+\cos<(\alpha+\beta)>\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin<(\alpha-\beta)>+\sin<(\alpha+\beta)>\bigg)\\\\ \hline \end\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin <|l|r|>\hline &\\ \sin<2\alpha>=\dfrac<2\mathrm\, \alpha><1+\mathrm^2\, \alpha> & \cos<2\alpha>=\dfrac<1-\mathrm^2\, \alpha><1+\mathrm^2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(x\pm \dfrac<\pi>3\right)>\\\\ \hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \end\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

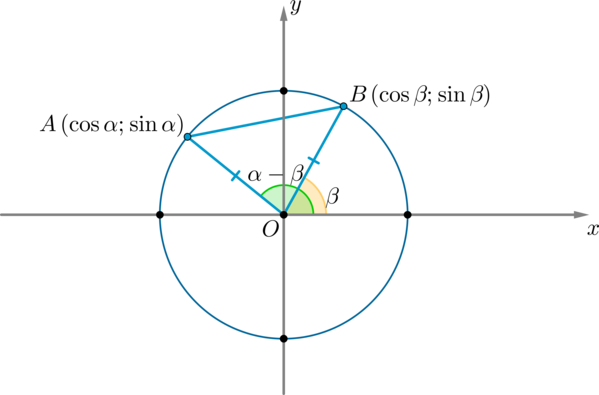
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos<(\alpha -\beta)>=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)

Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\) .

Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\) . По теореме косинусов:

\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства \((1)\) и \((2)\) :

Отсюда и получается наша формула.

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :

разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne 0\)
(при \(\cos\alpha=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\mp \mathrm\,\beta\) , при \(\cos\beta=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\pm \mathrm\,\alpha\) ):

Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\) .

5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\) , выводится формула котангенса суммы/разности двух углов.

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\) , получим еще две формулы для косинуса двойного угла:

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm\,2\alpha=0\) ):

Таким образом, эта формула верна только при \(\cos\alpha\ne 0\) , а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm\,2\alpha\) ).

По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\) .

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

\(\blacktriangleright\) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)

Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .

\(\blacktriangleright\) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

\(\blacktriangleright\) Вывод формул суммы/разности функций:

Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)

2) Так же, только делением на \(\sin^2\alpha\) , выводится формула для косинуса.

\(\blacktriangleright\) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

Рассмотрим выражение \(a\sin x+b\cos x\) . Домножим и разделим это выражение на \(\sqrt\,\) :

\(a\sin x+b\cos x=\sqrt\left(\dfrac a<\sqrt>\sin x+ \dfrac b<\sqrt>\cos x \right)=\sqrt\big(a_1\sin x+b_1\cos x\big)\)

Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\) , т.к. \(\left(\dfrac a<\sqrt>\right)^2+\left(\dfrac b<\sqrt>\right)^2=\dfrac=1\)

Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:

\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: \[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)

Источник