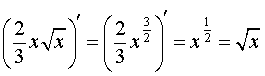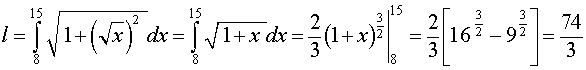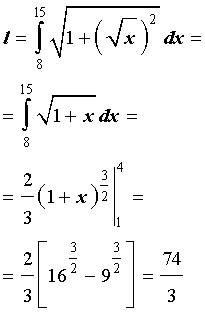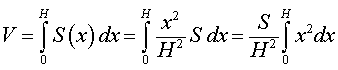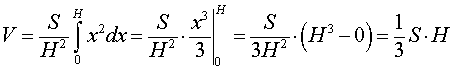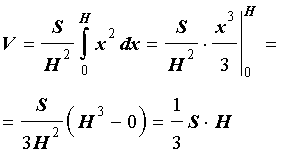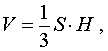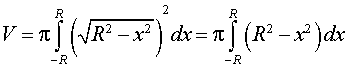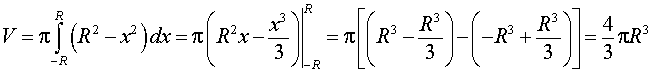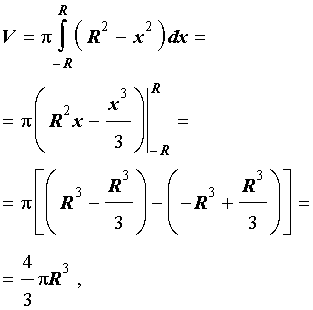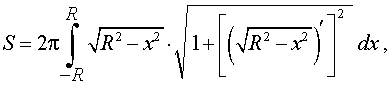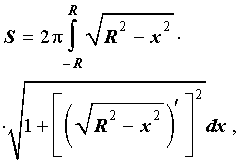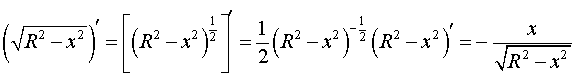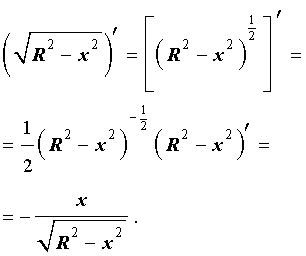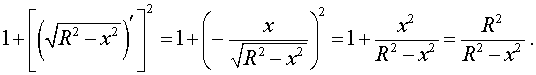- Объем пирамиды
- Геометрические приложения определенного интеграла
- Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
- Примеры решения задач на вычисление площадей фигур на плоскости
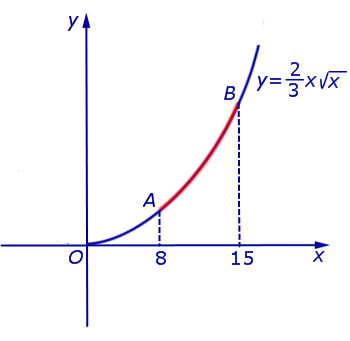
- Пример решения задачи на вычисление длины дуги кривой на плоскости
- Вывод формул для объема пирамиды и для объема шара
- Вывод формулы для площади сферы
Объем пирамиды
Теорема. Объём пирамиды равен произведению площади её oснования на треть её высоты.
Сначала докажем эту теорему для пирамиды треугольной, а затем и многоугольной.
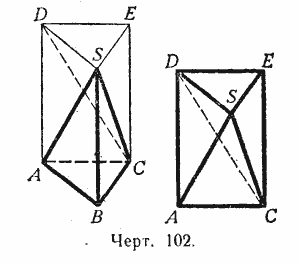
1) На основании треугольной пирамиды SABC (черт. 102) построим такую призму SABCDE, у которой высота равна высоте пирамиды, а одно боковое ребро совпадает с ребром SB. Докажем, что объём пирамиды составляет третью часть объёма этой призмы. Отделим от призмы данную пирамиду. Тогда останется четырёхугольная пирамида SADEC (которая для ясности изображена отдельно). Проведём в ней секущую плоскость через вершину S и диагональ основания DC. Получившиеся от этого две треугольные пирамиды имеют общую вершину S и равные основания DEC и DAC, лежащие в одной плоскости; значит, согласно доказанной выше лемме пирамиды эти равновелики. Сравним одну из них, именно SDEC, с данной пирамидой. За основание пирамиды SDEC можно взять \(\Delta\)SDE; тогда вершина её будет в точке С и высота равна высоте данной пирамиды. Так как \(\Delta\)SDE = \(\Delta\)АВС, то согласно той же лемме пирамиды SDEC и SABC равновелики.
Призма ABCDES нами разбита на три равновеликие пирамиды: SABC, SDEC и SDAC. (Такому разбиению, очевидно, можно подвергнуть всякую треугольную призму. Это является одним из важных свойств треугольной призмы.) Таким образом, сумма объёмов трёх пирамид, равновеликих данной, составляет объём призмы; следовательно,
где Н есть высота пирамиды.
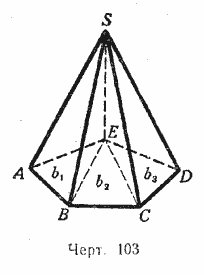
2) Через какую-нибудь вершину Е (черт. 103) основания многоугольной пирамиды SABCDE проведём диагонали ЕВ и ЕС.
Затем через ребро SE и каждую из этих диагоналей проведём секущие плоскости. Тогда многоугольная пирамида разобьётся на несколько треугольных, имеющих высоту, общую с данной пирамидой. Обозначив площади оснований треугольных пирамид через b1, b2 , b3 и высоту через Н, будем иметь:
Следствие. Если V, В и Н означают числа, выражающие в соответствующих единицах объём, площадь основания и высоту какой угодно пирамиды, то
Теорема. Объём усечённой пирамиды равен сумме объёмов трёх пирамид, имеющих высоту, одинаковую с высотой усечённой пирамиды, а основаниями: одна — нижнее основание данной пирамиды, другая — верхнее основание, а площадь основания третьей пирамиды равна среднему геометрическому площадей верхнего и нижнего оснований.
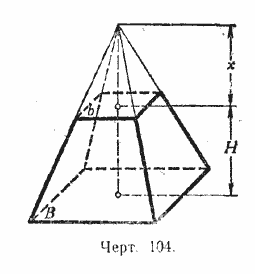
Пусть площади оснований усечённой пирамиды (черт. 104) будут В и b, высота Н и объём V (усечённая пирамида может быть треугольная или многоугольная — всё равно).
Требуется доказать, что
где √ Bb есть среднее геометрическое между B и b.
Для доказательства на меньшем основании поместим малую пирамиду, дополняющую данную усеченную пирамиду до полной. Тогда объём усечённой пирамиды V мы можем рассматривать как разность двух объёмов — полной пирамиды и верхней дополнительной.
Обозначив, высоту дополнительной пирамиды буквой х, мы найдём, что
Для нахождения высоты х воспользуемся теоремой из раздела, согласно которой мы можем написать уравнение:
Для упрощения этого уравнения извлечём из обеих частей его арифметический квадратный корень:
Из этого уравнения (которое можно рассматривать как пропорцию) получим:
Подставив это выражение в формулу, выведенную нами для объёма V, найдём:
Так как В — b = (√ B + √ b ) (√ B — √ b ), то по сокращении дроби на разность √ B — √ b получим:
т. е. получим ту формулу, которую требовалось доказать.
Источник
Геометрические приложения определенного интеграла
 Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла |
 Примеры решения задач на вычисление площадей фигур на плоскости Примеры решения задач на вычисление площадей фигур на плоскости |
 Пример решения задачи на вычисление длины дуги кривой на плоскости Пример решения задачи на вычисление длины дуги кривой на плоскости |
 Вывод формул для объема пирамиды и для объема шара Вывод формул для объема пирамиды и для объема шара |
 Вывод формулы для площади сферы Вывод формулы для площади сферы |
Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
В данном разделе справочника приведена таблица, содержащая формулы, с помощью которых можно вычислить:
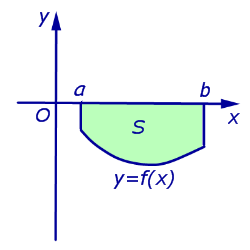
Площади криволинейных трапеций различного вида (площади фигур, ограниченных графиками функций);
Длины дуг кривых на плоскости;
Объемы тел, если известны площади их поперечных сечений;
Объемы тел, полученных при вращении криволинейных трапеций вокруг оси абсцисс Ox ;
Площади поверхностей тел, полученных при вращении графиков функций вокруг оси абсцисс Ox .
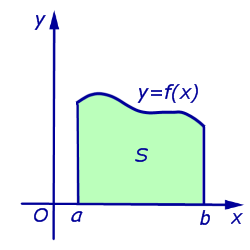
| Рисунок | Формула | Описание | |||||||
 | 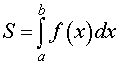 | ||||||||
 |  | ||||||||
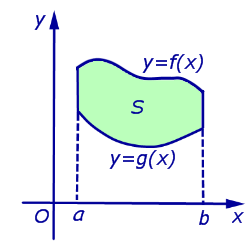 | 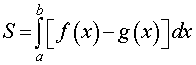 | ||||||||
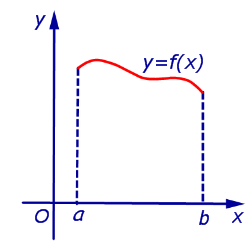 | 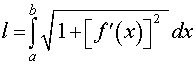 | ||||||||
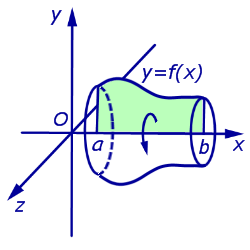 | 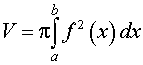 | ||||||||
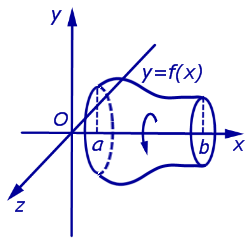 | 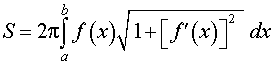 |
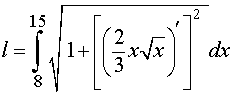 | (1) |
Подставим найденную производную в формулу (1), а затем вычислим полученные интегралы при помощи таблицы неопределенных интегралов и формулы Ньютона — Лейбница:
Ответ .
Вывод формул для объема пирамиды и для объема шара
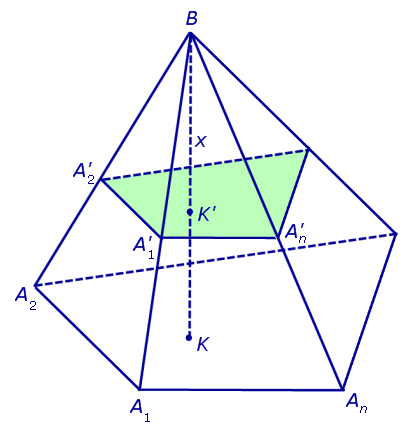
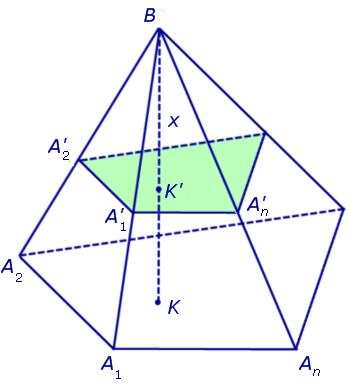
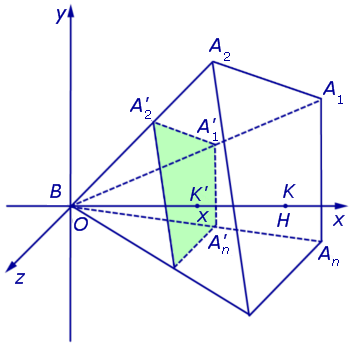
Решение . Рассмотрим произвольную n — угольную пирамиду BA1A2 . An с вершиной B, высота BK которой равна H, а площадь основания A1A2 . An равна S. Обозначим через S (x) площадь сечения 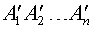
Поскольку многоугольники 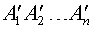
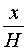
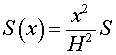 | (2) |
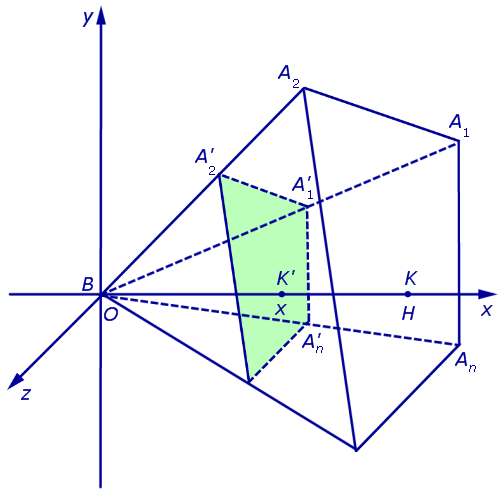
Рассмотрим теперь в пространстве систему координат Oxyz и расположим нашу пирамиду BA1A2 . An так, чтобы ее вершина B совпала с началом координат O, а высота пирамиды BK оказалась лежащей на оси Ox (рис. 5).
Тогда сечение 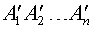
Итак, мы получили формулу для объема пирамиды
котрой пользовались в различных разделах справочника.
Замечание . Совершенно аналогично выводится формула для объема конуса. Формулы для объема прямой призмы объема прямой призмы и для объема цилиндра вывести таким способом еще проще, поскольку у них все сечения, перпендикулярные высоте, равны между собой. Мы рекомендуем провести эти выводы читателю самостоятельно в качестве полезного упражнения.
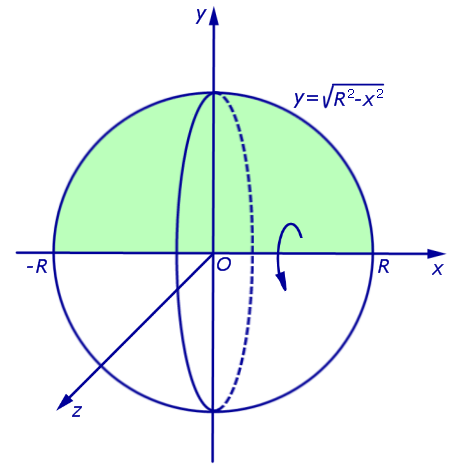
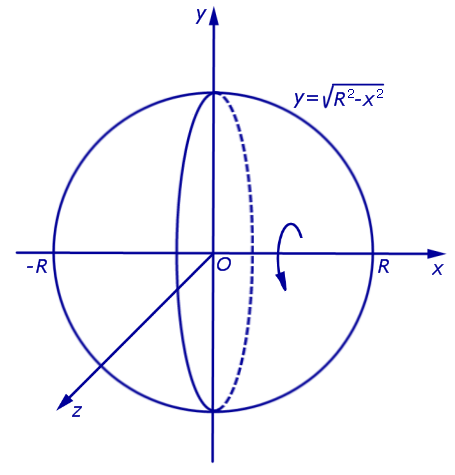
Пример 5 . Вывести формулу для объема шара радиуса R, воспользовавшись формулой для вычисления объема тела вращения.
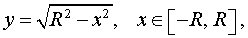 | (3) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O. Шар радиуса R получается в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции (3) и ограниченной снизу отрезком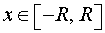
что и должно было получиться.
Вывод формулы для площади сферы
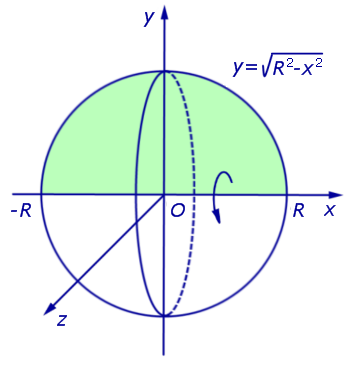
Решение . Снова рассмотрим функцию
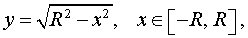 | (4) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O (рис. 7).
Поскольку сфера радиуса R получается в результате вращения вокруг оси Ox графика функции (4), то в соответствии с формулой для вычисления площади поверхности тела вращения получаем
Подставим найденную производную в выражение, стоящее под знаком квадратного корня:
Таким образом, подынтегральная функция принимает вид:
Источник

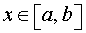 ,
,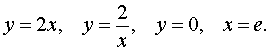
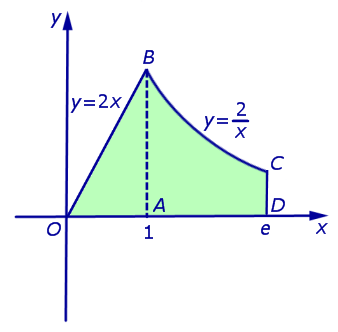
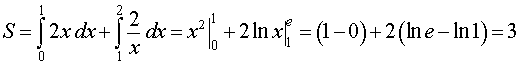
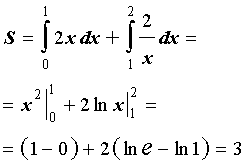
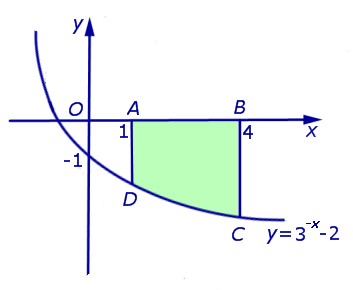
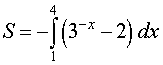 .
.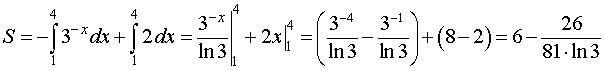
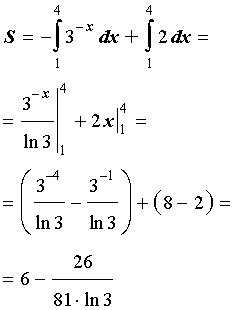
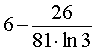 .
. , 8 .
, 8 .