- Как найти площадь шестиугольника по формуле?
- Немного фактов из истории
- Площадь правильного 6-угольника
- Расчет
- Как находить площадь неправильного шестиугольника
- Метод трапеции
- Использование осей координат
- Разбивка шестиугольника на другие фигуры
- Площадь равностороннего шестиугольника
- Нахождение площади правильного шестиугольника: формула и примеры
- Общая формула вычисления площади
- Площадь правильного шестиугольника, вписанного в окружность
- Примеры задач
- Правильный шестиугольник: свойства, формулы, площадь
- Правильный шестиугольник и его свойства
- Площадь правильного шестиугольника – формула и расчет онлайн
- Определение и построение
- Геометрия шестиугольника
- Немного фактов из истории
- Пятиугольник в реальности
- Как найти площадь многогранника при известных координатах вершин
- Общая формула вычисления площади
- До начала вычислений
- Площадь пентагона
- Пентагон
- Школьная задача
- Примеры шестиугольников
- Расчет
- Шестиугольник, выпуклый и невыпуклый шестиугольник:
- Площадь правильного шестиугольника, вписанного в окружность
- Площадь правильного 6-угольника
- Другие способы нахождения площади неправильного шестиугольника
- Первый вариант
- Свойства простые и интересные
Как найти площадь шестиугольника по формуле?
С вопросом: «Как найти площадь шестиугольника?», можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами. В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
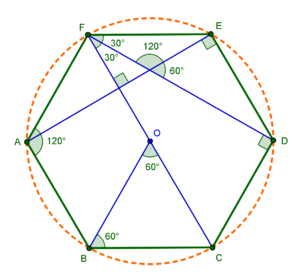
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности.
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Чтоб рассчитать S , пользуются следующей формулой:
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапеции
Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координат
Используем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Источник
Нахождение площади правильного шестиугольника: формула и примеры
Правильный шестиугольник – это геометрическая фигура; правильный многоугольник с 6 равными углами и сторонами.
Общая формула вычисления площади
Площадь (S) правильного шестиугольника вычисляется по формуле ниже, где a – длина его стороны:
Формула получена следующим образом:
Правильный шестиугольник состоит из шести равных равносторонних треугольников. Площадь каждого рассчитывается так:
Следовательно, площадь правильного шестиугольника равна:
Площадь правильного шестиугольника, вписанного в окружность
Сторона правильного шестиугольника равняется радиусу окружности, описанной вокруг него (a=r).
Это значит, что формула площади может быть представлена в таком виде (а заменяем на r):
Примеры задач
Задание 1
Сторона правильного шестиугольника равна 8 см. Найдите его площадь.
Решение:
Используем первую формулу, в которой задействована длина стороны:
Задание 2
Вычислите площадь правильного шестиугольника, ели радиус описанной вокруг нее окружности равен 15 см.
Решение:
Воспользуемся второй формулой (через радиус окружности):
Источник
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
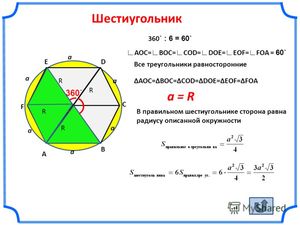
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Источник
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов \(n\) –угольника равна \(180^\circ(n-2)\) , то каждый угол правильного \(n\) –угольника равен \[\alpha_n=\dfrac
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен \(\dfrac <4-2>4\cdot 180^\circ=90^\circ\) ;
каждый угол правильного шестиугольника равен \(\dfrac<6-2>6\cdot 180^\circ=120^\circ\) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если \(a\) – сторона правильного \(n\) –угольника, \(R\) и \(r\) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: \[\begin
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: \(a=R\) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны \(120^\circ\) .
4. Площадь правильного шестиугольника со стороной \(a\) равна \(\dfrac<3\sqrt<3>><2>a^2\) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу \(r\) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный \(60^\circ\) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный \(n\) -угольник инвариантен относительно поворота на угол \(\dfrac<360^\circ>
Источник
Площадь правильного шестиугольника – формула и расчет онлайн
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Геометрия шестиугольника
Шестиугольник — фигура на плоскости, ограниченная шестью равными отрезками, которые пересекаются под углом 120 градусов. Изучением многоугольников в целом и гексагона в частности занимался отец геометрии Евклид, который в «Началах» предложил способ построения правильного шестиугольника при помощи циркуля и линейки.
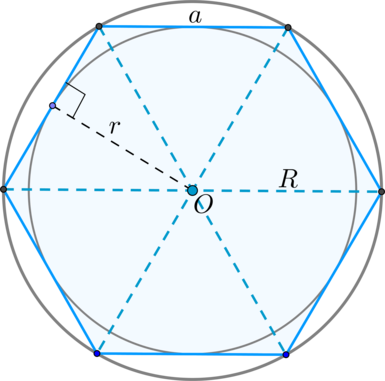
Вокруг любой правильной геометрической фигуры можно описать окружность или вписать ее внутрь. Гексагон не исключение. Сторона фигуры a и радиусы описанной окружности R и вписанной r соотносятся как:
Главная особенность гексагона состоит в том, что сторона многоугольника и радиус описанной окружности абсолютно равны, так как 2sin(pi/6) = 1.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Пятиугольник в реальности
Невыпуклые геометрические фигуры редко встречаются в человеческой повседневности и обычно представляют собой основания для нестандартных призм. Наиболее распространенным пятиугольником в реальности считается пентагон — правильный многоугольник. Пентагон нашел применение в архитектуре и дизайне, и тезкой фигуры является одно из самых известных зданий Америки — штаб министерства обороны США.
Додекаэдр — платоново тело, каждая из 12 сторон которого является правильным пятиугольником. Додекаэдр используется в различных сферах, но наиболее известным представлением многогранника считается игральная кость d12, которая используется как генератор случайных чисел для настольных ролевых игр.
Несмотря на то, что многие организмы обладают пентасимметрией, например, морские звезды или плоды мушмулы, природные пятиугольные объекты практически не встречаются в природе.
Как найти площадь многогранника при известных координатах вершин
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
Общая формула вычисления площади
Площадь (S) правильного шестиугольника вычисляется по формуле ниже, где a – длина его стороны:
Формула получена следующим образом:
Правильный шестиугольник состоит из шести равных равносторонних треугольников. Площадь каждого рассчитывается так:
Следовательно, площадь правильного шестиугольника равна:
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Площадь пентагона
Площадь любой геометрической фигуры — это количественная оценка того, какую часть плоскости ограничивают ее стороны. Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле:
S = n/4 × a 2 × ctg(pi/n),
где n – количество сторон фигуры, a – длина стороны.
Таким образом, если подставить n = 5 и выразить получившееся выражение десятичной дробью, мы получим простую формулу для вычисления площади пентагона:
где a — длина одной стороны.
Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как:
Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных:
- радиус вписанной окружности;
- радиус описанной окружности;
- длина стороны.
Рассмотрим на примерах, как вычислить площадь правильного пятиугольника.
Пентагон
Штаб министерства обороны США — это всемирно известное здание, которое имеет форму правильного пятиугольника. Каждая сторона штаба имеет длину 281 м и мы без проблем можем узнать, какую площадь занимает здание. Для более удобного представления выразим длину в километрах, введем эти данные в форму калькулятора a = 0,281 и получим результат:
Площадь Пентагона составит 0,136 квадратных километров.
Школьная задача
К примеру, необходимо вычислить площадь пентагона, зная, что радиус вписанной окружности составляет 15 см. Мы можем выразить сторону многоугольника через простое соотношение радиуса вписанной окружности и длины стороны a = 1,4131 r, после чего посчитать по формуле его площадь. Проще всего ввести значение радиуса в ячейку «Радиус вписанной окружности r» и получить мгновенный результат:
Кроме непосредственно площади фигуры, калькулятор автоматически подсчитал остальные атрибуты пятиугольника.
Примеры шестиугольников
Гексагон — довольно распространенная геометрическая фигура. В человеческой повседневности форму шестиугольника принимают грани таких объектов как гайки, карандаши или детали машин. В природе шестиугольную форму имеют пчелиные соты, снежинки, а также кристаллические решетки некоторых соединений углерода. Кроме того, существует уникальное космическое явление на Сатурне — гигантский гексагон, который представляет собой атмосферный вихрь в виде правильного шестиугольника.
Шестиугольник — эффективная фигура, позволяющая замостить поверхность без пробелов или наложений. Кафель или тротуарная плитка часто принимают форму гексагона, однако наиболее выдающимся примером замощения поверхности шестиугольником является Мостовая гиганта — памятник природы, образованный соединением более 40 000 базальтовых колонн. Шестиугольные колонны Мостовой гиганта образовались в результате древнего извержения вулкана и элегантно замостили поверхность североирландского побережья.
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Чтоб рассчитать S , пользуются следующей формулой:
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза – 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Площадь правильного шестиугольника, вписанного в окружность
Сторона правильного шестиугольника равняется радиусу окружности, описанной вокруг него (a=r).
Это значит, что формула площади может быть представлена в таком виде (а заменяем на r):
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами. В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности.
Другие способы нахождения площади неправильного шестиугольника
- Например, если мы выяснили, что площадь правильного треугольника — 60 см 2 , а площадь отсутствующего треугольника — 10 см 2 , то: 60 см 2 – 10 см 2 = 50 см 2 .
- Если известно, что в шестиугольнике не хватает точно одного треугольника, то его площадь можно найти, умножив общую площадь на 5/6, так как мы имеем 5 и 6 треугольников. Если не хватает двух треугольников, то умножаем на 4/6 (2/3) и так далее.
- Один из видов неправильного шестиугольника состоит из двух параллелограммов. Для нахождения их площадей просто перемножьте основания на высоты и затем сложите их площади.
Первый вариант
Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Источник

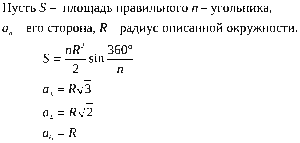














 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;


























