Как вывести индексы numpy

8. Индексация, срезы, итерирование

Одномерные массивы очень похожи на простые списки Python:

Многомерные массивы имеют один индекс на одну ось, поэтому обращение к элементам и извлечение срезов производится не по одному а по нескольким индексам:

Те же правила действуют и для многомерных массивов. Результаты могут показаться немного необычными, но это связано с тем, что нам непривычно работать с массивами у которых больше трех осей. После некоторой практики это быстро проходит:

Если указать количество индексов меньше количества осей, то недостающие индексы считаются полными фрагментами как если бы вместо них было указано : — т.е. отсутствующие индексы считаются полными срезами.

Иногда приходится иметь дело с массивами размерность которых больше 3. В таких случаях для обращения к элементам приходится указывать длинные списки индексов:

Для удобства NumPy позволяет заменять последовательности из : на .

Итерирование многомерных массивов выполняется только по первой оси

Если необходимо выполнить итерирование по каждому элементу, то можно воспользоваться атрибутом flat , который сжимает массив до одной оси:

8.1. Дополнительные возможности индексирования

Работая с последовательностями: строками, списками или кортежами, мы привыкли только к одному единственному способу индексирования, который предлагает нам Python. Неужели это можно сделать как-то по другому? Оказывается можно, и, иногда это оказывается гораздо удобнее чем может показаться. Помимо индексирования целыми числами и срезами, к которому мы так сильно привыкли, NumPy предлагает еще два необычных метода индексирования. Первый — это индексация с помощью массивов целых чисел, а второй — это индексация с помощью массивов булевых значений.

8.1.1. Индексирование массивами целых чисел

Что такое массив индексов? Массив индексов — это обычный массив (последовательность) целых чисел, причем каждое число соответствует некоторому индексу определенного элемента в другом массиве, например:

Но на практике, чаще, гораздо удобнее использовать в качестве массивов индексов не массивы NumPy, а списки Python. Относительно вышеприведенного примера это будет выглядеть следующим образом:

Немного необычно, но зато очень удобно. В самом деле, не будь у нас такого способа индексирования, то для составления подобных массивов, каждый раз пришлось бы писать что-то подобное:

Как видно, в таких случаях индексация с помощью массивов оказывается гораздо удобнее. Причем индексы массивов могут содержать любое количество осей и элементов по этим осям:

Если в некотором массиве есть вложенные подмассивы, то их так же можно индексировать с помощью массивов целых чисел:

Если нам нужно добраться до элементов, которые находятся в его вложенных массивах, т.е. задавать индексы для нескольких измерений, то мы можем воспользоваться индексацией с помощью нескольких массивов целых чисел. Но в таком случае появляется дополнительное требование — массивы индексов должны иметь одинаковые размеры.

Более того, при индексации мы можем указывать не только числа, массивы и даже срезы, но и их комбинации:

Если мы используем несколько массивов для индексирования, то эти массивы можно объединить в последовательность:

Но если мы просто упакуем эти массивы в новый массив NumPy, то это вполне может сработать, но не всегда, потому что новый массив индексов интерпретируется как индексирование самой первой оси массива и если ее размер меньше, чем наибольшее число в индексе массивов, то это приведет к ошибке.

Индексирование с помощью массивов можно применять для изменения элементов исходного массива:

Если массив индексов содержит повторы, то изменение одного элемента происходит несколько раз, пока не будет присвоено последнее значение:

В данном примере элемент a[0] менялся три раза, сначала ему было присвоено значение 7, потом 8 и наконец 9.

Над элементами, которые указаны в массиве индексов можно выполнять математические операции:

В примерах выше, было бы гораздо удобнее использовать вместо выражения a[[1, 3, 6]] = a[[1, 3, 6]] + 10 его сокращенный вариант a[[1,3,6]] += 10 и это действительно возможно. Но оба варианта выражений делают не совсем то, что можно было бы ожидать. Можно предположить, что если в массиве индексов содержатся повторы, то и математические операции так же будут повторяться, но этого не происходит:

Казалось бы, что в первом случае к a[0] единица прибавится два раза и два раза будет вычтена во втором случае, но вместо двух раз это произошло всего лишь один раз. Такое поведение связано с тем, что по правилам Python запись a += 1 должна быть эквивалентна a = а + 1 . То есть, сколько бы раз мы не обращались к a[0] и меняли его, при следующем обращении к a[0] мы будем иметь дело с элементом исходного массива, а не его измененным значением. Даже если индексы указаны во так: a[[0, 0, 1, 0]] , то любая математическая операция над a[0] будет выполнена всего один раз.

8.1.2. Индексация массивами булевых значений

Булевых значений всего два, это False и True . Возникает весьма интересный вопрос, как с помощью таких массивов выполняется индексация, ведь они состоят из одних лишь логических значиний. И снова, оказывается не только возможно, но и крайне удобно в некоторых случаях:

Выглядит не совсем убедительно. Хорошо, вот другой пример:

Скорее всего, именно при выполнении логических операций над массивами такой метод индексирования окажется наиболее полезным. Тем более, что всегда можно воспользоваться его коротким вариантом:

Однако, использование сложных логических выражений в качестве массива индексов все же возможно, достаточно воспользоваться логическими операторами: and , or , xor или not . Выражение a[10 можно переписать, как a[(10 , что, казалось бы, обязано работать, но:

Дело в том, что операторы and , or , xor и not выполняют логические операции целиком над всем объектом, а не его отдельными элементами. Звучит как какая-то ересь, но для выполнения сложных логических выражений нам придется пользоваться побитовыми логическими операторами: & (and), | (or), ^ (xor) и

(not). Такая необходимость возникает потому что массив булевых значений это прежде всего массив, а учитывая тот факт что абсолютно все в языке Python является объектами, то этот массив так же будет объектом. Но выполняя сложные логические выражения мы их выполняем не над всем массивом (объектом) целиком, а над элементами, которые находятся внутри него. А учитывая, что внутри находятся булевы значения, которые в сво очередь в языке Python являются обычными числами 1 — True и 0 — False:

То нам ничего не мешает рассматривать эти булевы значения как обычные единичные биты информации, а следовательно и выполнять над ними побитовые операции. Значит выражение a[(10 переписанное, как a[(10 просто обязано сработать:

И это замечательно. Так как теперь можно выполнять логические выражения любой сложности:

>>> a[(a%2 == 1) & (a%3 == 2) & (a%4 == 3)] array([11, 23])

Мы уже видели, что индексация с помощью массива позволяет использовать в качестве его элементов числа, срезы, а так же другие массивы индексов. Теперь к таким элементам добавляются еще и булевы массивы. Вот только, нужно помнить, что если мы хотим выбрать какието элементы на определенной оси индексируемого массива, то все нужные и ненужные элементы должны быть перечисленны в одномерном булевом массиве. Понятно, что количество элементов в таком булевом массиве, должно быть равно количеству элементов по необходимой оси.

Здесь можно долго ломать голову, но оказывается, что если мы собрались использовать массивы i и j в одном массиве индексов [i, j] (а не [i][j] ), то количество элементов True в массивах i и j должно совпадать. Причем получается не совсем то, что можно было бы ожидать:

Все равно, не слишком то понятно как это работает. Давайте попробуем разобраться:

В данном случае извлекаются не все элементы на пересечении букв «Т», а только по одному из каждой строки. Соответствующие элементы из i и j образуют что-то вроде координат:

Не знаю где, но наверняка, существуют задачи где это может очень пригодиться, тем более такая индексация выполняется на языке C т. е. гораздо быстрее чем аналогичная на Python.

Источник

Индексация, срезы, итерирование массивов

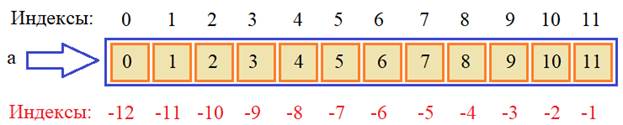
На этом занятии познакомимся со способами считывания и записи значений в массивы NumPy. В целом синтаксис очень похож на обращение к элементам списков языка Python. Давайте рассмотрим все на конкретных примерах. Предположим, что имеется одномерный массив:

И мы хотим прочитать отдельные его элементы. Это можно сделать путем обращения к нужному элементу массива по его индексу, например, так:

Помимо положительных индексов существуют еще и отрицательные, которые отсчитывают элементы с конца списка, например:

Если мы выходит за пределы массива и указываем несуществующий индекс, то возникает исключение (ошибка):

Соответственно, если нужно изменить значение какого-либо элемента, то ему просто присваивается это новое значение:

Как видите, здесь применяется тот же синтаксис, что и при работе с обычными списками Python. То же касается и срезов. Мы можем выделять и менять сразу группу элементов массива. Общий синтаксис срезов выглядит так:

Давайте посмотрим примеры использования этой конструкции:

Здесь указан начальный индекс 2, конечный индекс 4 и по умолчанию берется шаг, равный 1. На выходе получаем массив из двух значений 2 и 3. Последний граничный индекс 4 не включается в срез.

Обратите внимание, в NumPy срезы возвращают новое представление того же самого массива, то есть, данные, на которые ссылаются переменные a и b одни и те же. Мы в этом можем легко убедиться, выполнив вот такую строчку:

и это приводит к изменению соответствующего элемента массива a:

array([ 100, 1, -100, 3, 4, 5, 6, 7, 8, 9, 10, 11])

Поэтому срезы – это не копии массивов, а лишь создание их нового представления. Это сделано специально для экономии памяти.

Другие примеры срезов:

Я, думаю, общий принцип использования одномерных срезов понятен. Разумеется, срезам можно присваивать новые значения. Например, так:

Элементы массива NumPy можно перебирать с помощью цикла for, так как массивы – итерируемые объекты. Например:

Индексация и срезы многомерных массивов

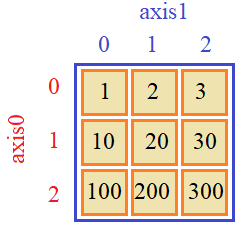
В базовом варианте индексация и срезы многомерных массивов работают также как и в одномерных, только индексы указываются для каждой оси. Например, объявим двумерный массив:

Для обращения к центральному значению 20 нужно выбрать вторую строку и второй столбец, имеем:

Чтобы взять последнюю строку и последний столбец, можно использовать отрицательные индексы:

Если же указать только один индекс, то получим строку:

Эта запись эквивалентна следующей:

То есть, не указывая какие-либо индексы, NumPy автоматически подставляет вместо них полные срезы.

Для извлечения столбцов мы уже должны явно указать полный срез в качестве первого индекса:

Итерирование двумерных массивов можно выполнять с помощью вложенных циклов, например:

Если же необходимо просто перебрать все элементы многомерного массива, то можно использовать свойство flat:

У массивов более высокой размерности картина индексации, в целом выглядит похожим образом. Например, создадим четырехмерный массив:

Тогда для обращения к конкретному элементу следует указывать четыре индекса:

Для выделения многомерного среза, можно использовать такую запись:

Это эквивалентно записи:

Если же нужно задать два последних индекса, то полные срезы у первых двух осей указывать обязательно:

Пакет NumPy позволяет множество полных подряд идущих срезов заменять троеточиями. Например, вместо a[:, :, 1, 1] можно использовать запись:

Это бывает удобно, когда у массива много размерностей и нам нужны последние индексы.

Списочная индексация

Помимо указания у массивов обычных индексов или срезов в NumPy существует еще один способ индексирования – через списки или массивы целых чисел. Чтобы лучше понять, о чем идет речь, рассмотрим этот механизм на примерах. Для простоты возьмем одномерный массив с какими-нибудь значениями:

Далее, смотрите, если указать обычный числовой индекс, то получим одно значение соответствующего элемента:

Но, если вместо числового индекса указать список:

то на выходе уже имеем массив из одного первого значения. Причем, этот массив будет копией, а не представлением исходного массива. То есть, выполняя операции:

Изменение массива b не приведет к изменению данных в массиве a.

А что будет, если в списке указать несколько индексов? Например, так:

На выходе получаем новый массив, состоящий из соответствующих значений. Или, можно сделать даже так:

То есть, мы здесь имеем, фактически, способ формирования новых массивов на основе других массивов. В списке достаточно перечислить индексы нужных элементов и на выходе формируется массив с соответствующими значениями. В ряде случаев такая операция бывает очень удобной.

Кроме обычных списков языка Python мы можем передавать и массивы NumPy, состоящие из целых значений. Например, так:

Или, с булевыми значениями:

В результате останутся только те элементы, которым соответствуют индексы True. Причем, длина списка (или массива) bIndx должна совпадать с длиной массива a, иначе произойдет ошибка.

Последний вариант списочной индексации используется очень часто. Например, мы можем сформировать массив индексов путем какой-либо булевой операции над массивом:

А, затем, использовать его, чтобы оставить только нужные элементы:

Или, все это можно записать короче в одну строчку:

Как видите, это невероятно удобный механизм обработки данных массивов пакета NumPy.

Списочная индексация и многомерные массивы

Фактически, массив индексов определяет значения и форму создаваемого массива. Например, если взять тот же одномерный массив:

но набор индексов определить как двумерный массив:

то на выходе будет формироваться уже двумерный массив:

Только в этом случае индексы i должны определяться именно массивом NumPy, а не списком Python.

Так можно создавать массивы любых размерностей. Давайте теперь посмотрим, как будет себя вести списочное индексирование с многомерными массивами. Возьмем двумерный массив:

и одномерный список индексов:

На выходе получим массив:

array([[ 9, 10, 11, 12],
[ 5, 6, 7, 8],
[ 1, 2, 3, 4]])

Смотрите, здесь индексы обозначают номера строк двумерного массива. В результате, строки нового массива идут в обратном порядке. Далее, пропишем индексы в виде двумерного массива:

Результатом будет трехмерный массив:

array([[[ 5, 6, 7, 8],
[ 1, 2, 3, 4]],
[[ 9, 10, 11, 12],
[ 5, 6, 7, 8]]])

Что здесь произошло? В действительности, каждый индекс двумерного массива соответствует определенной строке этого массива. А двумерная форма индексов лишь указывает как упаковать строки в новом массиве. То есть, вместо каждого индекса подставляется своя строка и получается трехмерный массив.

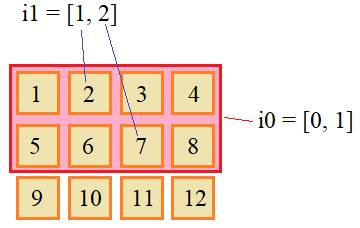
Если же мы хотим выбирать из двумерного массива не строки, а отдельные элементы и на их основе формировать новые массивы, то следует использовать два списка. Первый список по прежнему будет указывать строки массива, а второй – индексы столбцов у каждой строки. Например, так:

Работу такого списочного индексирования можно представить в виде:

При множественной списочной индексации допускается указывать конкретные индексы и срезы. Например:

В этом случае получим уже матрицу 3×2, то есть, второй список i1 здесь используется для выделения столбцов целиком, а не одного только элемента. Соответственно, строчка:

выделим массив из двух значений 2 и 6.

Изменение массивов через списочную индексацию

С помощью списков можно не только создавать новые массивы, но и менять значения в исходном. Например, возьмем одномерный массив:

и изменим его следующие элементы:

Смотрите, как это удобно. Мы сразу списком индексов обозначаем изменяемые элементы и присваиваем им соответствующие новые значения.

Если в списке индексов имеются повторы, то новое значение будет каждый раз переписываться, пока не дойдет до последнего:

Здесь в первый элемент трижды записывались числа: 1, 2 и 3. Но, если выполнить вот такую операцию:

то число 3 будет прибавлено только один раз. При арифметических операциях пакет NumPy «понимает», что первому элементу нужно просто прибавить значение 3 и трижды это делать не надо. Или же можно записать такую математическую операцию:

В этом случае элементам с индексами 0, 1 и 2 будет прибавлена 1. Здесь также первому элементу единица добавляется только один раз, несмотря на то, что индекс указан дважды. Вот это следует иметь в виду при работе с массивами NumPy.

Те же самые математические операции и операции присваивания можно выполнять и с многомерными массивами. Работает все аналогичным образом.

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Источник