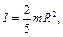Как вывести расчетную формулу скорости

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник

Вывод расчетных формул

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ КИНЕМАТИЧЕСКИХ ВЕЛИЧИН ТЕЛ,

СКАТЫВАЮЩИХСЯ С НАКЛОННОЙ ПЛОСКОСТИ

При изучении материала уясните, что любое движение твердого (недеформируемого) тела может быть представлено как наложение поступательного и вращательного движений.

При поступательном движении любая прямая, мысленно проведенная в теле, перемещается параллельно самой себе, при этом тело может двигаться как прямолинейно, так и криволинейно.

При поступательном движении все точки тела движутся с одинаковыми скоростями и ускорениями. Поэтому для кинематического описания поступательного движения тела достаточно описать движение какой-либо одной точки. Обычно описывают движение центра масс (центра инерции) тела, под которым понимают такую точку, в которой можно считать сосредоточенной всю массу тела, а все внешние силы – приложенными к ней.

Необходимо иметь в виду, что в отличие от поступательного при вращательном движении все точки твердого тела движутся по окружностям, центры которых расположены на одной прямой, называемой осью вращения. При этом ось может быть как неподвижной, так и двигаться. В последнем случае говорят, что тело вращается около движущейся оси. Например, вращение цилиндра, катящегося по наклонной плоскости.

При подготовке к лабораторной работе также изучите закон сохранения механической энергии. Он применим в системе взаимодействующих тел при выполнении следующих условий:

а) система должна быть замкнутой (на тела системы не действуют внешние силы или суммарная работа всех внешних сил равна нулю);

б) внутри системы могут действовать консервативные силы (сила тяжести, сила упругости, сила гравитационного взаимодействия), работа которых не зависит от формы траектории;

в) внутри системы должны отсутствовать неконсервативные (диссипативные) силы, в частности сила трения (кроме сил трения покоя) и силы неупругих деформаций, иначе механическая энергия системы будет рассеиваться, превращаясь во внутреннюю энергию.

Вывод расчетных формул

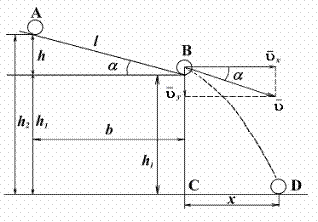
В данной работе рассматривается скатывание тел с наклонной плоскости (рис. 1.1). Если угол a наклона плоскости мал, то при движении отсутствует скольжение. Между телом и плоскостью в точках их соприкосновения возникает трение, являющееся трением покоя. Так как эти точки в каждый момент времени неподвижны, то сила трения, действующая на катящееся тело, работы не совершает. Поэтому полная энергия катящегося тела остается постоянной.

Поскольку тело совершает вращение и его центр масс, через который проходит ось вращения, перемещается поступательно, кинетическая энергия складывается из энергии поступательного и вращательного движений.

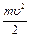
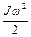
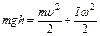
Согласно закону сохранения механической энергии, потенциальная энергия тела на вершине плоскости (в точке А) равна сумме кинетической энергии поступательного движения тела и кинетической энергии вращательного движения тела :

, (1.1)

где m – масса скатывающегося тела;

g – ускорение свободного падения;

u – линейная скорость центра масс тела в точке В;

I – момент инерции тела относительно оси вращения;

w – угловая скорость вращения тела.

Так как скольжение отсутствует, то

, (1.2)

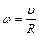
где R – радиус катящегося тела.

Из формул (1.1) и (1.2) следует, что

. (1.3)

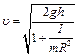
Момент инерции тел, обладающих симметрией вращения, можно записать в виде

,

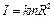
где k – безразмерный коэффициент.

;

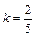
для тонкостенного полого цилиндра

;

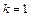
для сплошного цилиндра

,

.

, (1.4)

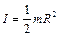
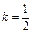
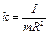
получим формулу для скорости тела в точке В:

. (1.5)

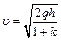
Движение тела по наклонной плоскости будет равноускоренным, так как происходит под действием постоянной силы – силы тяжести. Для равноускоренного движения без начальной скорости

; (1.6)

, (1.7)

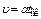
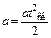
где l – длина пути по наклонной плоскости;

а – ускорение центра масс тела;

t_ск – время скатывания тела по наклонной плоскости АВ.

Из выражений (1.6) и (1.7) следует, что

, (1.8)

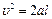
тогда из формул (1.5) и (1.8) получим:

, (1.9)

. (1.10)

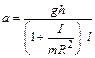
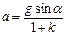
Время скатывания тела по наклонной плоскости АВ определим из формул (1.5), (1.6), (1.10):

. (1.11)

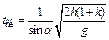
Из формул (1.5), (1.10), (1.11) видно, что u, t_ск и а зависят от формы тела (коэффициент k) и не зависят от его массы и размеров.

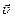
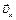
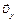
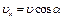
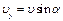
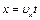
Скорость тела в точке В можно также определить из законов движения тела по траектории BD. Для этого вектор скорости разложим на вертикальную и горизонтальную составляющие. Движение по параболе BD можно рассматривать как равномерное в горизонтальном направлении с постоянной скоростью и равноускоренное в вертикальном направлении с начальной скоростью и ускорением g. Путь при равномерном движении определяется по формуле

, (1.12)

а при равноускоренном –

, (1.13)

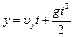
где t – время свободного полета тела по кривой BD;

х – горизонтальная дальность полета тел;

у – путь, проходимый телом по вертикали ВС.

Подставляя значения u_x и u_у в уравнения (1.12) и (1.13), получим:

; (1.14)

. (1.15)

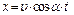
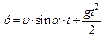
Выразив из уравнения (1.14) время:

,

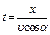
и подставив в формулу (1.15), получим:

(1.16)

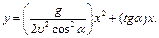
Полученное уравнение есть уравнение параболы. Таким образом, тело, скатившись с наклонной плоскости, дальше движется по ветви параболы BD.

Из уравнения (1.16) найдем скорость тела в точке В по экспериментальным данным. Обозначим эту скорость :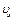

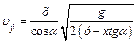
. (1.17)

ОПРЕДЕЛЕНИЕ

Дата добавления: 2016-08-23 ; просмотров: 5783 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник