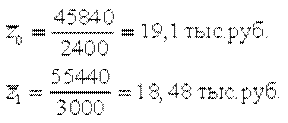Расчет индекса цен: примеры, формулы, онлайн-калькулятор
Быстрая навигация по странице:
Система индексов цен
Контроль цен имеет важное значение в экономике. Комплекс показателей статистики цен состоит их широкого спектра критериев, позволяющих изучить различные аспекты величины, изменения и структуры стоимости товаров и услуг. В процессе исследования изучаются розничные цены и тарифы, оптовые, отпускные, закупочные, сметные, мировые и другие виды цен. Одним из важнейших инструментов такого анализа выступают различные индексы цен: Ласпейреса и Пааше, агрегатные и средние из индивидуальных, Фишера и т.п. Изменение средних цен исследуется посредством системы следующих индексов: переменного состава, постоянного состава и структурных сдвигов (данные показатели взаимосвязаны). В целом рассчитываемые показатели являются относительными, которые отражают соотношение уровней какого-либо явления во времени или в пространстве и позволяет выполнить сравнение фактических значений с эталонными, плановыми, прогнозными и т.п. величинами. По степени охвата рассматриваемые показатели могут быть как индивидуальными (при расчете, например, для конкретного товара), так и сводными (при расчете значений, например, по группе товаров). По базе сравнения рассматриваемые показатели относятся к динамическим (например, при анализе изменения стоимости набора продуктов питания за различные периоды времени), но могут рассчитываться и территориальные значения. По форме построения рассматриваемые показатели могут быть как агрегатными, так и средними.
Размещено на www.rnz.ru
Индексы, полученные с использованием формулы Ласпейреса, достаточно широко применяются для контроля над потребительскими ценами и инфляцией: в РФ, например, именно на основе данной методики рассчитывается официальный индекс потребительских цен (ИПЦ). Также данная методика нашла широкое применение при определении динамики цен производителей промышленной продукции. Индексы, полученные с использованием формулы Пааше, как правило, включают более широкий спектр продукции и услуг. При их расчете в качестве весов берется не структура потребительских затрат, а структура объема продаж, или добавленной стоимости, или выпущенной продукции в текущем периоде, поэтому они могут быть вычислены только после окончания отчетного периода. Показатель, определенный по методике Пааше, применяется для исследования изменения стоимости составляющих компонентов ВВП; закупочных цен в аграрном секторе экономики; сметных — в строительной индустрии; а также цен, используемых для внешнеэкономической деятельности. Значение индекса, полученного по формуле Ласпейреса, как правило, выше, чем значение показателя по формуле Пааше. Такая систематическая зависимость двух указанных показателей называется эффектом Гершенкрона.
Формула индекса цен
В зависимости от вида индекса можно использовать несколько формул, позволяющих вычислить индекс цен. Так, при расчете индивидуальных индексов используют следующую формулу:

Для расчета значения сводного (общего, агрегатного) индекса цен применяется формула Пааше:

В силу специфики правового регулирования индекс потребительских цен в РФ рассчитывается на основе формулы Ласпейреса (Ласпейраса):

Модифицированная формула, применяемая для практических вычислений при проведении статистического наблюдения, приводится в Приказе Росстата от 30.12.2014 N 734 «Об утверждении Официальной статистической методологии организации статистического наблюдения за потребительскими ценами на товары и услуги и расчета индексов потребительских цен».
Пример расчета индекса цен
Исходные данные: имеется следующая информация о реализации товаров предприятиями города:
| Продукция | Базисный период | Отчетный период | ||
|---|---|---|---|---|
| Стоимость единицы, руб. | Количество, шт. | Стоимость единицы, руб. | Количество, шт. | |
| Товар №1 | 25 | 15 | 22 | 17 |
| Товар №2 | 18 | 24 | 19 | 25 |
| Товар №3 | 16 | 45 | 18 | 44 |
На основе исходных данных определить индивидуальные и общий индекс цен, индекс потребительских цен, потери покупателей от роста цен (или экономию в случае их снижения).
Составим таблицу вспомогательных расчетов:
| Продукция | Базисный период | Отчетный период | p0q0 | p1q0 | p0q1 | p1q1 | ||
|---|---|---|---|---|---|---|---|---|
| Стоимость единицы (p0), руб. | Реализовано единиц (q0) , ед. | p1, руб. | q1, ед. | |||||
| Товар №1 | 25 | 15 | 22 | 17 | 375 | 330 | 425 | 374 |
| Товар №2 | 18 | 24 | 19 | 25 | 432 | 456 | 450 | 475 |
| Товар №3 | 16 | 45 | 18 | 44 | 720 | 810 | 704 | 792 |
| Итого | — | — | — | — | 1527 | 1596 | 1579 | 1641 |
Вычислим индивидуальные индексы цен:
ip товар №1 = 22 : 25 = 0,88 — стоимость товара №1 снизилась на 12%;
ip товар №2 = 19 : 18 = 1,056 — стоимость товара №2 выросла на 5,6%;
ip товар №3 = 18 : 16 = 1,125 — стоимость товара №3 выросла на 12,5%.
Общий (агрегатный) индекс цен рассчитаем по формуле Пааше:
Стоимость товаров в среднем увеличилась на 3,9%. Потери покупателей от повышения стоимости товаров составили 1641 — 1579 = 62 руб.
Индекс потребительских цен рассчитаем по формуле Ласпейреса:
Ip = ∑p1q0 : ∑p0q0 = 1596 / 1527 = 1,045. Полученное значение индекса показывает, что уровень потребительской инфляции по рассматриваемой группе товаров составил 4,5%.
Онлайн калькулятор индекса цен
Для вычисления агрегатного индекса цен и индекса потребительских цен приводим простую форму онлайн-калькулятора, используя который, Вы можете самостоятельно выполнить расчет данных показателей и заполнить таблицу. Для получения правильных результатов работы онлайн-калькулятора в процессе ввода данных необходимо внимательно соблюдать размерность полей, что позволит выполнить необходимые вычисления быстро и точно. Дробные величины должны вводиться с ТОЧКОЙ, а не с запятой! В представленной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает расчет индекса потребительских цен онлайн. Для вычисления указанных показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет».
Источник
Средние индексы и индексы средних показателей



Средний индекс — это индекс, вычисленный как средняя величина из индивидуальных индексов.
При исчислении средних индексов используются две формы средних: средняя арифметическая и средняя гармоническая.
Средний арифметический индекс будет тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.
Зависимость для определения среднего арифметического индекса физического объема продукции будет иметь вид:
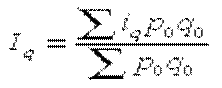
Поскольку iq × q0 = q1 , то формула этого индекса легко преобразуется в полученную ранее
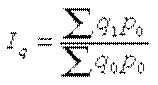
Пример расчета среднего индекса цен и физического объема продукции по данным табл. 9.1:

Средние индексы широко используются при анализе рынка ценных бумаг. Наиболее известными являются индексы Доу—Джонса, Стандард и Пур, индекс акций высокотехнологичной фирмы «НАСДАК» и др.
Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени.
Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:
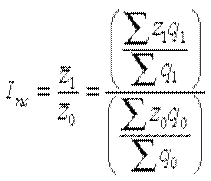
где Iпс — индекс переменного состава.
Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае — себестоимости), но и структуры совокупности (весов).
Индекс постоянного (фиксированного) состава — это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции рассчитывается по формуле:
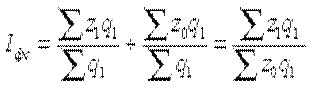
где Iфс — индекс фиксированного состава.
Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения только структуры изучаемого явления на динамику среднего уровня этого явления. Например, индекс изменения среднего уровня себестоимости определяется по формуле:
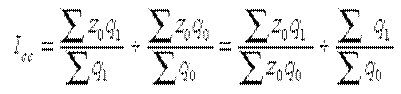
где Iсс — индекс структурных сдвигов.
Система взаимосвязанных индексов имеет следующий вид:
Пример 9.1 . Пусть имеются данные о себестоимости единицы продукции на трех предприятиях в текущий и базисный периоды (табл. 9.2).
Количество произведенной продукции и себестоимость единиц продукции одного вида по трем предприятиям отрасли
| Номер предприятия | Произведено продукции | Себестоимость единицы продукции, тыс. руб. | Индивидуальные индексы себестоимости, % Iz = z1 / z0 | Издержки производства, млн. руб. | ||
| Всего единиц | % к итогу | Базисный период, z0 | Текущий период, z1 | Базисный период, z0q0 | Текущий период, z1q1 | z0q1 |
| Базисный период, q0 | Текущий период, q1 | Базисный период | Текущий период | |||
| А | 7 = 6 / 5 | 8 = 5 × 1 | 9 = 6 × 2 | 10 = 5 × 2 | ||
| 20,3 | 101,5 | 33,6 | 30,45 | |||
| 18,4 | 102,2 | 8,64 | 11,04 | 10,8 | ||
| 15,5 | 103,3 | 3,6 | 13,95 | 13,5 | ||
| Всего | 54,2 | 45,84 | 55,44 | 54,3 |
На текущий период по сравнению с базисным себестоимость производства продукции возросла на каждом предприятии (гр. 5—6); изменилась структура производства; уменьшилась доля первого предприятия в общем выпуске продукции, возросла доля третьего, а доля второго уменьшилась (гр. 3—4).
Рассчитаем индекс переменного состава. Для этого сначала определим среднюю себестоимость единицы продукции в текущий и базисный периоды:
Тогда Iпс = 18,48 × 19,1 = 0,9675, или 96,75%.
Следовательно, средняя себестоимость по трем предприятиям снизилась в текущий период по сравнению с базисным на 3,25%, несмотря на то, что на каждом из них в отдельности она возросла. Это объясняется тем, что исчисленный индекс, помимо прочего, учитывает дополнительно влияние структурного фактора.
Рассчитаем индекс себестоимости фиксированного состава:
Iфс = 55,44 / 54,3 = 1,021, или 102,1%.
Таким образом, себестоимость в текущий период по сравнению с базисным возросла на 2,1%.
Рассчитаем влияние изменения структуры на динамику средней себестоимости:
Iсс = (54,3/45,84) / (3000/2400) = 0,9476, или 94,76%.
Изменение доли предприятий в общем объеме произведенной продукции привело к снижению себестоимости на 5,24%.

Аналогично строятся системы индексов для других показателей.
Источник
9.6. Средние индексы
Во всех случаях, когда информация о физических объемах в натуральном исчислении отсутствует, для определения изменения показателей используется средняя форма индексов.
В практических расчетах используются два вида средних
средний индекс качественного показателя, •
средний индекс физического объема.
Каждый из средних индексов может быть рассчитан по формулам средней арифметической взвешенной или средней гармонической взвешенной.
Средний индекс физического объема используется в тех случаях, когда отсутствует информация об объемах выпуска в натуральных измерителях.
Средняя арифметическая форма индекса физического объема применяется, когда имеется информация о стоимости реализованной продукции в базисном периоде, и об индивидуальных индексах физического объема iq. Формулу среднеарифметического индекса физического объема можно получить на основе агрегатного индекса физического объема Ласпейреса
I — Z 91 Р» , заменив физические объемы текущего периода на их Z 90 ^0
выражение через индивидуальный индекс физического объема iq.
i — — , следовательно q1 — / • 90;
где iq — усредняемая величина, а p0 •q0 — статистический вес.
Полученная формула является формулой среднеарифметического индекса.
Среднеарифметический индекс показывает, во сколько раз в среднем изменится физический объем в планируемом (предстоящем) периоде.
Разница между числителем и знаменателем характеризует изменение стоимости продукции в планируемом периоде.
AP9q — ZVP0 9-Z90 • Р0 .
Пример расчета среднеарифметического индекса физического объема.
Известна стоимость реализованной продукции в текущем периоде (товаров А, В и С) и планируемое изменение физических объемов в предстоящем периоде, в % (таблица 9.2.).
продукц ии Продукция текущего к. периода, тыс.
руб. Изменение физического объема в планируемом периоде, % Вспомогательные расчеты i _ 4-
9o ? PO • 9o А 24ooo +io 1,1 264oo В 4oooo +5 1,o5 42ooo С 15ooo -2o o,8 12ooo Z 79ooo — — 8o4oo для каждого товара
По данным таблицы 9.2 рассчитаем
индивидуальным индекс: i _-
Тогда величина среднеарифметического индекса физического 8o4oo
объема составит I4 _
_ 1,oi8, — в планируемом периоде
Z 9o • p o 79ooo
прирост объема продукции в среднем по данной группе товаров составит приблизительно 1,8%, что соответствует общей сумме прироста объема продаж Apqq _ 8o4oo — 79ooo _ 14ooтыс. руб. Этот прирост произойдет за счет
изменения физических объемов продаж.
Средний индекс физического объема можно рассчитать по формуле средней гармонической взвешенной. Она применяется в случае, если исходная информация представлена индивидуальными индексами физического объема iq (или их легко рассчитать), или фактической
стоимостью продукции текущего периода q • p\.
Формула среднего геометрического индекса физического объема
может быть получена из агрегатной формы общего индекса физического объема Пааше : Z 9i • p\
o которая показывает, во сколько раз изменяется стоимость продукции за счет изменения физических объемов.
В указанной формуле физические объемы базисного периода q0 заменяются их выражением через индивидуальный индекс физического объема:
Таким образом, средний гармонический индекс физического объема рассчитывается по формуле:
где iq — усредняемая величина; p1 • q1 — статистический вес.
Разница между числителем и знаменателем дает показатель среднего изменения стоимости в текущем периоде за счет изменения физического объема:
Apqp = Z qr P1-Z — •qr P1.
Пример расчета: необходимо определить среднее изменение стоимости продукции за счет изменения физических объемов продаж в текущем периоде по данным, приведенным в таблице 9.3.
Данные для расчета среднего геометрического индекса физического
продукции Продукция текущего периода, P1 • q1 дьгс.
руб. Изменение в текущем периоде, % iq 1
‘q А 24000 +20% 1,2 0,833 20000 В 40000 + 12,5% 1,25 0,80 32000 С 15000 -25% 0,75 1,33 20000 Итого 79000 — — — 72000 Iq = Z q1- P1 = 79000 = 1,097 = 109,7%.
Общий прирост стоимости продукции в текущем периоде за счет изменения физических объемов составил Apqp = 79000 — 72000 = 5000 тыс.
руб. Такое же значение прироста стоимости продукции получаем по формуле агрегатного индекса физического объема Пааше.
Содержание и расчет среднего индекса качественного показателя рассмотрим на примере цен.
Общий индекс цен в средней арифметической форме используется в плановых расчетах (при прогнозировании).
Информация для расчета должна быть представлена в виде индивидуальных индексов цен или планируемых изменений цен и стоимости продукции базисного периода (отчетного).
Формулу для расчета общего индекса цен в средней арифметической форме легко получить преобразованием формулы агрегатного индекса цен
Ласпейреса IP = , выразив цены отчетного периода P1 через
индивидуальные индексы цен i и цены базисного периода p0 : i = — ,
следовательно P1 = iP • p0 .
где iP — усредняемая величина, P0 q0 — статистический вес усредняемой величины. Средний арифметический индекс цен показывает, во сколько раз в среднем изменится стоимость продукции предстоящего периода за счет изменения цен. Разность числителя и знаменателя Apqp = Zipq0 • P0 -Z q0 • P0
определяет общее изменение стоимости продукции предстоящего (планового) периода за счет изменения цен.
Пример расчета: известны объемы продаж и цены на продукцию по 3-м видам товаров, данные приведены в таблице 9.4. Данные для расчета среднего арифметического индекса цен Вид Объем продаж Оптовые цены Вспомогательные товара в текущем расчеты периоде, шт. Текущие
Л ip ip • pO • qo А 24000 20 22 1,1 26400 В 40000 16 20 1,25 50000 С 15000 10 10 1,0 15000 Итого 79000 — — — 91400 I = 91400 = 1Д57 = 115,7% . p 79000
В предстоящем периоде средний рост стоимости продукции за счет роста цен составит 115,7% или Apqp = 91400 — 79000 = 12400 тыс. руб. Средняя гармоническая форма общего индекса цен используется, когда информация представлена в виде индивидуальных индексов цен или их изменений и стоимости продукции текущего периода pl • q1.
Формулу для расчета среднего гармонического индекса цен можно получить преобразованием агрегатного индекса цен Пааше, заменив цены базисного периода p0 его выражением через индивидуальный индекс цен
ip. Так как ip =—, то p0 = —; следовательно
Z P1 • q1 = Z P1 • q1
Средний гармонический индекс цен Ip показывает, во сколько раз в
среднем изменилась стоимость продукции текущего периода за счет изменения цен:
Разность между числителем и знаменателем формулы показывает абсолютное изменение стоимости продукции за счет изменения цен
Ap = Z q1 • л-Z у- • q1 • P1 .
Пример расчета индекса цен в гармонической форме приведен в таблице 9.5.
Таблица 9.5. Расчет среднего гармонического индекса цен Вид продукции Стоимость продукции, тыс. руб. Изменение цен в
текущем периоде, % Расчет индексов Po •qo P1 •q ‘Р = P
‘P А 18000 24000 11 1,11 21600 В 30000 40000 7 1,07 37500 С 20000 15000 Не изменились 1,00 15000 Итого 68000 79000 — — 74100 — 79000
По данным таблицы 9.5. I = = 1,066 = 106,6%, следовательно,
в текущем периоде изменение цен привело к росту стоимости продукции в 1,066 раза или на Ар = 79000 — 74100 = 4900 тыс. руб.
Источник