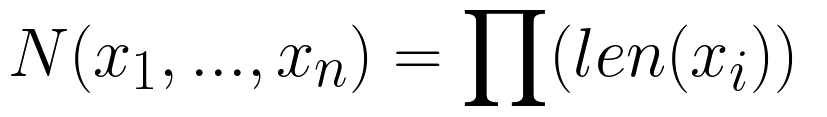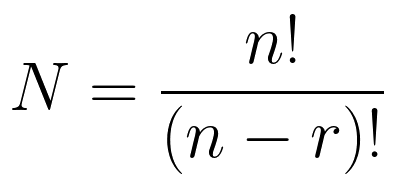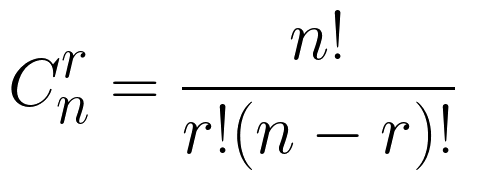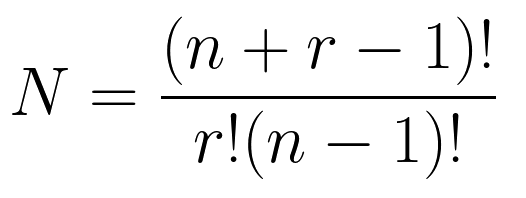Как вывести все возможные комбинации python

Использование модуля Itertools Python

Модуль Python itertools очень полезен, если вы хотите создать разные типы итераторов, подходящие для различных задач. Также библиотека itertools содержит встроенные функции для вычисления перестановок и комбинаций.

В этом разделе мы рассмотрим некоторые полезные методы, которые генерируют итераторы.

Чтобы использовать этот модуль, мы должны сначала импортировать его. Он уже доступен в стандартной библиотеке, поэтому предустановлен.

Использование Python itertools.chain() для объединения итераций

Метод Python itertools.chain() генерирует итератор из нескольких итераций.

Это просто связывает все итераторы вместе в одну последовательность и возвращает единственный итератор для этой объединенной последовательности.

Синтаксис этого метода следующий

Давайте посмотрим на простой пример.

Здесь мы используем итератор напрямую, перебирая его, используя for item in .

Хотя мы получаем содержимое наших списков правильно, значения словаря не отображаются.

Чтобы исправить это, мы могли бы использовать dict.items() для получения кортежа пар (key, value) .

Теперь у нас также есть напечатанные значения.

Для генерации последовательности на основе счетчика

Мы можем использовать функцию Python itertools.count() чтобы сделать итераторы соответствующими itertools.count() .

Здесь это итератор, который ведет счет бесконечно, начиная с 0 и далее. Продолжает увеличивать счет на step=1 . Мы также можем установить десятичное или отрицательное число.

Например, если вы хотите доказать, что у вас бесконечный цикл, вы можете запустить приведенный ниже фрагмент, но это НЕ рекомендуется.

Просто убедитесь, что itertools.count() считается бесконечно.

Использование этой функции может не сразу показаться вам очевидным, вы можете комбинировать ее с другими функциями, такими как метод zip, для создания последовательностей.

Рассмотрим пример ниже:

Здесь вы можете увидеть мощь итераторов. Поскольку итераторы производят выходные данные только по запросу, мы можем использовать zip() с другой конечной итерацией, например списком.

Теперь это используется для создания индексов для элементов в списке.

Теперь, если вы хотите иметь подмножество последовательности итератора с помощью Python itertools.count() , вы также можете использовать itertools.islice() для создания только части итератора.

Как видите, обе последовательности идентичны. Это показывает, что у вас может быть несколько подходов к созданию последовательностей.

Для повторения значения

Предположим, вы хотите повторить определенное значение, вы можете создать итератор для повторяющегося значения, используя itertools.repeat(value) .

Например, если вы хотите построить последовательность вида (i, 5) , где i находится в диапазоне от 0 до 10, вы можете использовать эту функцию.

Действительно, нам удалось легко сделать эту последовательность.

Другой пример, в котором эта функция полезна, — если вы пытаетесь построить квадраты с помощью map() в Python.

Видите, как легко мы смогли построить его с помощью map() .

Использование itertools.tee() для клонирования последовательностей

Есть еще одна полезная функция под названием tee() , которая клонирует последовательность и производит две последовательности.

Это основано на команде Linux tee, которая клонирует свои выходные данные.

Здесь, когда вы клонируете последовательность с помощью tee() , вы не можете снова использовать тот же итератор. Вы должны быть очень осторожны при использовании этой функции.

Действительно, мы могли видеть две клонированные последовательности с одинаковыми выходами.

Перебор последовательности с помощью itertools.cycle()

Функция itertools.cycle() предоставляет итератор, который мы можем перебирать бесконечно. Это полезно, если вы хотите постоянно переключаться между состояниями в приложении.

Рассмотрим два состояния лампочки: «включено» и «выключено».

Вы можете создать итератор, который циклически перебирает два состояния при каждом нажатии переключателя.

Состояние лампочки постоянно меняется между двумя значениями «включено» и «выключено».

Как отфильтровать элементы с помощью takewhile() и drop while()

Мы можем использовать itertools.takewhile() Python itertools.takewhile() для фильтрации элементов последовательности, если условие True . Если условие становится False , фильтрация прекращается.

Вот простой пример, который фильтрует числа, если число положительное.

Здесь последовательность остановилась после 3, поскольку следующий элемент равен -1.

Точно так же itertools.dropwhile() фильтрует элементы, пока условие имеет значение False и возвращает все элементы после первого значения, отличного от false.

Создать комбинации с помощью combinations()

Мы также можем создавать последовательности комбинаций, используя Python itertools.combinations() .

Вот простой пример:

Если вы хотите, чтобы в комбинациях повторялись последовательные элементы, вы можете использовать combinations_with_replacement() .

Точно так же вы можете перечислить перестановки, используя permutations() и permutations_with_replacement() .

Поиск перестановок

Математически перестановка относится к «расположению определенных чисел или букв». Именно это и делает функция permutations() в библиотеке itertools .

Перестановки строки Python

Если есть строка в Python и нужно выяснить, как можно расположить ее буквы, то эту задачу легко решить с помощью функции permutations() .

Функция permutations() принимает аргумент String и предоставляет объект itertools . Если мы попробуем напечатать переменную ‘per’ напрямую, мы получим следующее:

Поэтому необходимо запускать цикл для печати каждой записи.

Перестановки нескольких чисел

Функция permuatations() принимает итеративный аргумент, поэтому для того, чтобы узнать перестановки чисел, нам нужно передать числа в виде списка, набора или кортежа.

В описанных выше методах вычисления перестановок мы включаем все числа или буквы. Есть возможность ограничить количество элементов в перестановках.

Перестановки с определенным количеством элементов

Подобно концепции ‘nPr’, которая гласит: «Размещение r элементов из n», это может быть достигнуто путем передачи целого числа после набора элементов.

В приведенном выше фрагменте кода функции permutations() предлагается упорядочить только 2 элемента за раз из предоставленного списка чисел.

Поиск комбинаций

Термин «Комбинации» относится к способам подбора элементов из набора объектов. Библиотека itertools предоставляет методы combinations() именно для этой функции.

Здесь следует отметить, что выбор набора объектов не требует их упорядочивания. Функция combinations() принимает два аргумента:

1. набор.
2. целое число, обозначающее количество значений, выбираемых для комбинации.

Комбинации букв в слове

Для данного слова, если нам нужно найти все комбинации, содержащие ровно 2 буквы из слова, то combinations() — это функция перехода.

Комбинации набора чисел

Подобно результатам комбинаций, которые мы получили для букв в слове, это может быть достигнуто для чисел в списке.

Примечание. Сгенерированные комбинации основаны на значениях индексов каждого объекта, а не на их фактических значениях, поэтому, если какое-либо значение повторяется, функция печатает аналогичные комбинации, считая, что каждое значение отличается.

Комбинации для повторяющихся номеров

Чтобы подробнее объяснить приведенное выше примечание, давайте запустим для него пример.

Результат не требует пояснений, поскольку числа в списке повторяются.

Комбинации элементов между собой

В библиотеке itertools есть еще одна функция, связанная с перестановками и комбинациями, называемая combinations_with_replacement() . Эта функция является разновидностью функции combinations() , с той небольшой разницей, что она включает комбинации элементов между собой.

Мы можем видеть четкое отличие вышеприведенного вывода от вывода с теми же параметрами при передаче в функцию combinations() .

Есть комбинации чисел, как будто их несколько экземпляров в списке. В основном это происходит потому, что, когда мы выбираем элемент из списка, вышеуказанная функция снова помещает то же значение, чтобы получить комбинации.

Еще пример. Наша задача — отобразить перестановку заданной строки. Здесь решаем эту проблему в python, используя перестановки встроенных функций (итерируемые).

Источник

Комбинаторика в Python

Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Короче, это все о сочетаниях, перестановках, числе способов и тому подобному.

Почему важна комбинаторика? Нет, не только лишь для решения олимпиадных задач, но также комбинаторика – один из столпов теории вероятностей, которая в свою очередь служит фундаментом для машинного обучения – одно из мощнейших трендов в ПО начале 21-го века!

В встроенном в Python модуле itertools существует ряд комбинаторных функций. Это:

• product() – прямое (Декартово) произведение одного или нескольких итераторов.
• permutations() – перестановки и размещения элементов множества.
• combinations() – уникальные комбинации из элементов множества.
• combinations_with_replacement() – комбинации с замещением (повторами, возвратами).

О каждой из них расскажу подробно. Для начала импортируем все нужные функции из модуля:

Прямое произведение

Прямое, или декартово произведение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств. Проще говоря мы берем из первого множества один элемент, а потом из второго выбираем элемент и составляем их в кортеж. Так вот все способы выбрать так элементы – составят декартово произведение. Пример:

Примечания. Во-первых, заметьте, что элементы следуют в строгом лексографическом порядке: сначала берется нулевой элемент из первой последовательности и сочетается с каждым по очереди из второй последовательности. Во-вторых, аргументами функции могут быть любые итерируемые объекты конечной длины. Я взял для примера список и строку, причем строка автоматически разбивается на символы.

В коде произведение множеств эквивалентно вложенным циклам:

Результат такой же, но рекомендую использовать именно библиотечную функцию, так как ее реализация, наверняка, будет лучше.

Вы можете передать в функцию больше последовательностей:

Каждый выходной элемент будет кортежем (даже в случае, если в нем только один элемент!). Также обратите внимание на то, что функция product (как и все остальные из сегодняшнего набора) возвращает не список, а особый ленивый объект. Чтобы получить все элементы, нужно преобразовать его в список функцией list:

Количество элементов на выходе будет произведением длин всех последовательностей на входе:

В функцию product можно передать именованный параметр repeat, который указывает сколько раз повторять цепочку вложенных циклов (по умолчанию один раз). Если repeat >= 2, то это называют декартовой степенью. То есть множество умножается на себя несколько раз. Так при repeat=2 эквивалентным кодом будет:

В таком случае количество элементов в результате будет вычисляться по схожей формуле с учетом того, что каждый множитель будет в степени repeat:

Перестановки

Функция permutations возвращает последовательные перестановки элементов входного множества. Первый элемент – будет исходным множеством. Второй – результат перестановки какой-то пары элементов и так далее, пока не будут перебраны все уникальные комбинации. Уникальность здесь рассматривается по позициям элементов в исходной последовательности, а не по и их значению, то есть элементы между собой алгоритмом не сравниваются. Важны только их индексы.

Число объектов остается неизменными, меняется только их порядок.

Второй параметр r отвечает за количество элементов в перестановках. По умолчанию будут выданы полные перестановки (длиной, равной длине n исходной последовательности), никакие элементы исходного множества не будут выброшены, а просто переставлены местами. Если задать 0

При r > n будет пустое множество, потому что невозможно из более короткой последовательности выбрать более длинную. Максимальное число вариантов – для полной перестановки равняется n! (факториал).

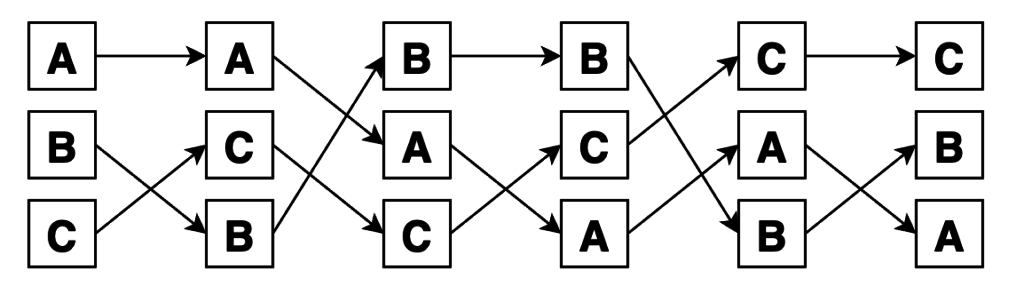
Размещения выглядят так. Сначала выбрали по 2 элемента из 3, а потом переставили их внутри групп всеми способами. Итого 6 вариантов:

Сочетания

combinations – функция, коротая выбирает все сочетания из входной последовательности. Пусть в ней имеется n различных объектов. Будем выбирать из них r объектов всевозможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по r, а их число равно:

Разница сочетаний и перестановок в том, что для сочетаний нам не важен порядок, а для перестановок он важен. Пример:

(1, 2) и (2, 1) – разные перестановки, но с точки зрения сочетаний – это одно и тоже, поэтому в combinations входит только один вариант из двух.

Второй параметр r – обязателен для этой функции. 0 n будет пустое множество.

Вот графический пример сочетаний из 3 по 2. Как видно, их вдвое меньше, чем размещений из 3 по 2, так как варианты с перестановками внутри групп не учтены по определению:

Сочетания с повторами

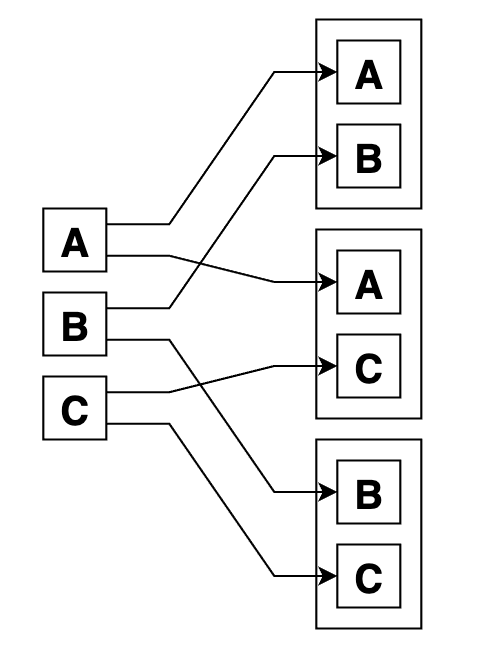
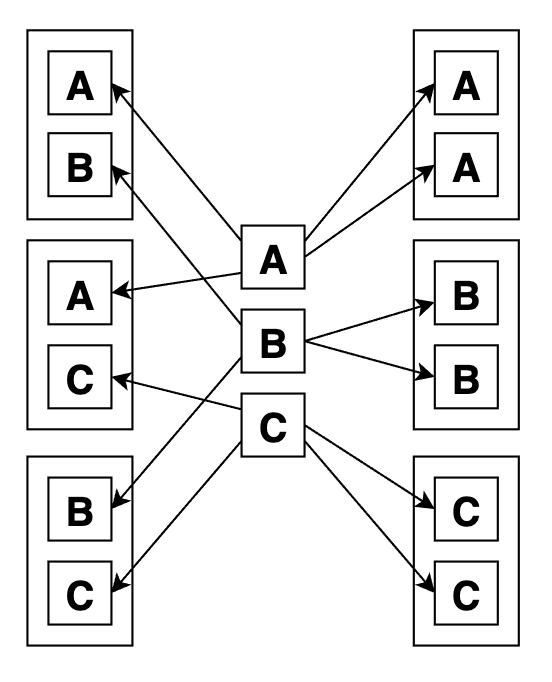
Функция combinations_with_replacement описывает, сколькими способами можно составить комбинацию по r элементов из элементов n типов (элементы в комбинации могут повторяться, но порядок их не важен). Обратите внимание на слово « тип «, в простых сочетаниях элементы не повторялись внутри одной выборки, они были как бы конкретными экземплярами.

На языке мешка с шарами, сочетания с повторами значит, что мы достаем шары из мешка, а потом кладем их обратно, записывая их цвета (цвет это и есть в данном случае аналог типа). Вполне может быть так, что мы достали красный шар два раза подряд, ведь после первого раза мы сунули его обратно в мешок. Пример:

Поэтому, имея возможность брать один и тот же элемент несколько раз, можно выбрать из последовательности в три элемента 4, и 5, и сколь угодно много (больше, чем было исходных типов). Например, по 4 из 2:

Вот графически сочетания с повторами по 2 из 3:

Формула числа элементов на выходе такова:

Бонус – брутфорс пароля

Как бонус предлагаю вам применение функции product() для брутфорса паролей. Сперва мы задаем набор символов, которые могут встречаться в пароле, наш алфавит, например такой:

А потом перебираем все возможные сочетания с длинами от минимальной до максимальной. Не забываем их склеить в строку:

Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈

Источник