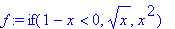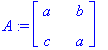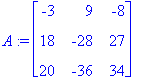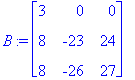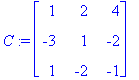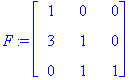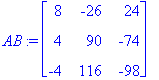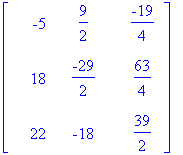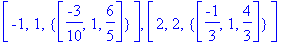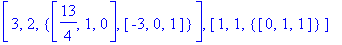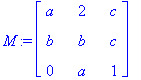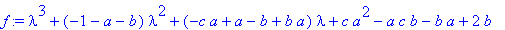Как вывести значение maple
Maple V представляет собой один из наиболее мощных математических пакетов Его возможности охватывают достаточно много разделов математики и могут с пользой применяться на разных уровнях, включая и уровень серьезных научных исследований.
Работать с ним можно как в режиме интерактивного диалога, так и путем составления и отладки программ на специальном Maple-языке, ориентированном на сложные математические вычисления.
Основу пакета составляет специальное ядро — программа символьных преобразований. Кроме того, имеется несколько тысяч специальных функций, хранящихся в подгружаемых к ядру пакетах и библиотеках.Общая ориентированность пакета на символьные преобразования (компьютерную алгебру) конечно не означает, что с помощью Maple нельзя решать задачи численно.
Maple умеет не только вычислять, но и обладает богатыми возможностями графического представления математических объектов и процессов.
Интерфейс пользователя
Здесь мы кратко рассмотрим лишь интерфейс пакета, работающего под Windows.
Окно Maple содержит многие атрибуты, привычные пользователю других приложений Windows: заголовочную часть, строку ниспадающих меню, панель управления, линейку вертикальной прокрутки, строку состояния и т.д. Основную часть базового окна занимает еще одно окно, в котором обычно располагаются один или несколько рабочих документов (Maple worksheet). В этом же окне могут располагаться окна помощи. Состояние ниспадающих и контекстного меню и кнопок на панели управления зависит от того, какое именно окно активно в настоящий момент и месторасположения курсора в окне Maple worksheet.
Рассмотрим наиболее типичный случай — работу пользователя с рабочим документом в режиме непосредственного диалога с программой. В этом случае на рабочем документе может быть представлена текстовая информация трех видов, а также объекты двумерной и трехмерной графики.
Исполняемые команды вводятся после специльного приглашения ‘ > ‘, красным цветом и должны заканчиваться точкой с запятой или двоеточием. Обычно команды вводятся в строчном формате, но пользователь имеет возможность перейти к специальному математическому формату ( который по умолчанию применяется при выводе). В одной строке может быть расположено более одной команды. Если после команды стоит двоеточие, то результат ее выполнения не будет отображен на экране. Если же после команды стоит точка с запятой, то после ее выполнения на экране появится результат. Если Maple не сможет вычислить введенное выражение, то результатом будет перевод введеннного выражения в матматический формат, принятый для вывода. Выходная информация печатается по умолчанию синим цветом. Исполнение Maple-команды инициируется нажатием ввода.
Команды можно объединять в исполняемые группы. Каждая такая группа выделяется слева общей для всех содержащихся в ней строк квадратной скобкой. Группа запускается на исполнение одним нажатием клавиши Enter и является по существу простейшей Maple-программой. Для того чтобы не исполнять каждую строку отдельно, а набрать целую исполняемую группу, достаточно осуществлять перевод строки с помощью комбинации клавиш Shift+Enter. Объединять исполняемые группы можно нажатием функциональной клавиши F4, а разбивать — нажатием F3. Разумеется, эти же действия можно проделать, выбрав соответствующие пункты в верхнем меню.
Текст черного цвета, которым написаны этот и предыдущие абзацы, используется для комментариев и никак не обрабатывается системой.
Для того чтобы вводить такой текст, достаточно, находясь в командной строке, нажать кнопку « Т « на панели управления, или вставить параграф, выбрав соответствющий пункт раздела «Insert» нисподающего меню.
Рабочий документ Maple можно структурировать, создавая вложенные друг в друга секции. Эти секции можно сворачивать. В свернутом виде каждая секция представлена лишь своим заголовком и признаком секции — кнопкой, снабженной знаком «+». Для разворачивания/сворачивания секции достаточно нажать на эту кнопку мышкой (впрочем, раз Вы читаете этот текст, то Вы, наверное, уже освоили эту возможность).
С помощью пункта меню «HyperLink. » из раздела » I nsert» можно создавать ссылки на определенные разделы других рабочих документов и топиков помощи. Тем самым Maple-документ может обладать структурой гипертекста.
Первые примеры
Рассмотрим простейшие примеры работы с Maple в интерактивном режиме:
Источник
Как вывести значение maple
Настоящее пособие посвящено работе с Maple в интерактивном режиме. Поэтому мы не будем здесь рассматривать внутренний язык программирования Maple в полном объеме. В частности, не будут затронуты вопросы написания и отладки процедур, объявления статуса переменных, создания библиотек и т.д. Мы рассмотрим лишь организацию основных алгоритмических структур: ветвлений и циклов. Используя эти конструкции в блоке команд Maple, объединенных в рабочую группу, мы, с одной стороны, продолжаем работать в интерактивном режиме, а с другой — фактически создаем простейшие программы.
Составной оператор условного перехода имеет структуру:
if then elif then . else fi ;
Здесь cond — выражение булевского типа, а block — любая группа команд Maple.
Конструкция elif then может повторяться несколько раз или вовсе отсутствовать. Часть else тоже не является обязательной.
Часто вместо составного оператора ветвления бывает удобнее использовать функцию ветвления — `if `. Она имеет три аргумента, первый из которых является условием, а второй и третий — возвращаемыми значениями. Если первый аргумент принимает значение true, то возвращаемым значением функции является второй аргумент, а если false — третий. Приведем пример использования функции `if ` :
В Maple существует несколько разновидностей циклов. Стандартный арифметический цикл имеет следующую структуру:
for from by to do od;
Здесь группа команд block выполняется для каждого значения переменной цикла var, которая меняется от значения exp1 до значения exp3 с шагом exp2. Если конструкция from и/или by отсутствует, то соответствующие им выражения принимаются равными 1. Отметим, что переменная цикла может изменять свое значение не только при переходе к следующему шагу цикла, но и внутри тела цикла. Проиллюстрируем это на примере:
> for i from 1 by 1 to 10 do i:=i+3 od;
Итерационный цикл имеет структуру:
while do od ;
Возможен и «гибрид» арифметического и итерационного циклов. Соответствующая конструкция имеет вид:
for from by while do od ;
Рассмотренные варианты организации циклов характерны (с теми или иными изменениями) для большинства языков программирования. Кроме них, в Maple имеется еще один специфический вид цикла. Как уже упоминалось, выражения в Maple имеют структуру дерева. Перебрать все ветви (операнды) первого уровня можно с помощью специального цикла, имеющего такой синтаксис:
for in do od ;
Проиллюстрируем работу этого цикла на примерах:
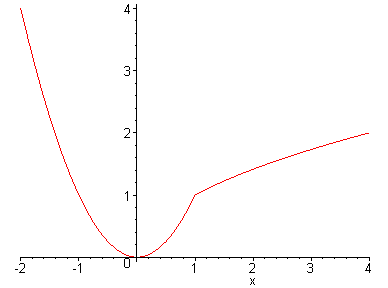
> for g in expand(f) do g od;
> s:=0:for i in numtheory[divisors](60) do if numtheory[mobius](i)=1 then s:=s+i fi od;s;
В последнем примере мы нашли сумму тех делителей числа 60, значение функции Мёбиуса от которых, равно 1.
В качестве иллюстрации использования циклов и условных операторов решим такую задачу: найти все пары простых чисел близнецов (так называют простые числа, отличающиеся друг от друга на 2) на отрезке натурального ряда чисел от 8000 до 9000.
8009, 8011
8087, 8089
8219, 8221
8231, 8233
8291, 8293
8387, 8389
8429, 8431
8537, 8539
8597, 8599
8627, 8629
8819, 8821
8837, 8839
8861, 8863
8969, 8971
Обратите внимание на то, что перед началом вычислений мы присвоили значение 0 зарезервированной переменной printlevel. Дело в том, что на команды, вызываемые из вложенных структур, не распространяется правило регулирования вывода результатов выполнения команды на экран с помощью помещения точки с запятой или двоеточия после соответствующей команды. В этом случае отображаются результаты выполнения всех команд, глубина вложенности которых не превышает текущего значения зарезервированной переменной printlevel. Это делается для того, чтобы программа не печатала слишком много промежуточных результатов. Если же мы все же хотим вывести на экран результаты, получаемые на глубине вложенности, превышающей значение printlevel, достаточно использовать оператор print. По умолчанию значение printlevel равно 1. (Именно этим объясняется, что в примере, где мы вычисляли сумму части делителей числа 60, не были отображены на экране результаты присваиваний s := s+i)
Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики
Источник
Как вывести значение maple
В состав Maple входит большое число специализированных пакетов, ориентированных, как правило, на конкретные разделы математики. Подгрузка пакета осуществляется с помощью команды with, аргументом которой служит имя пакета:
Warning, new definition for maximize
Warning, new definition for minimize
[basis, convexhull, cterm, define_zero, display, dual, feasible, maximize, minimize, pivot, pivoteqn, pivotvar, ratio, setup, standardize]
Нередко пакеты содержат функции, называющиеся так же, как функции, входящие в ядро Maple, но отличающиеся от них. В таких случаях после подгрузки пакета содержащиеся в них функции получают более высокий приоритет по сравнению со своими «тезками». В нашем примере система предупредила нас, что после подключения пакета линейной оптимизации будет действовать новое определение функций maximize и minimize .
В качестве результата успешного выполнения команды with Maple выводит на дисплей (курсивом в квадратных скобках) перечень функций, ставших доступными после активизации пакета.
Нередко пользователю нужны не все функции пакета, а лишь незначительная их часть. В этих случаях для экономии оперативной памяти компьютера полезно использовать команду with с несколькими аргументами. При этом первый из них по-прежнему будет означать имя подключаемого пакета, а остальные — имена тех функций пакета, которые следует подгрузить. Например, вместо нескольких десятков функций, входящих в состав пакета по теории чисел, можно подключить лишь несколько функций, интересующих пользователя в текущий момент:
> with(numtheory, divisors, factorset, phi, order, primroot);
[divisors, factorset, order, ф, primroot]
Возможно и «одноразовое» использование функции из специализированного пакета без сохранения ее в оперативной памяти после обращения. Для такого вызова необходимо указать имя пакета, сопроводив его именем вызываемой функции, заключенным в квадратные скобки:
При повторном вызове функции определителя (без указания пакета линейной алгебры, в котором она хранится). Maple «забыл», что такое det и посчитал ее пользовательской функцией.
Следует иметь в виду, что некоторые функции, «приписанные» к тем или иным специализированным пакетам, на самом деле доступны из ядра Maple. Таковы, например, функции ifactor, isolve, isprime, ithprime , nextprime и prevprime из пакета numtheory, matrix и vector из пакета linalg, инертные функции из пакета student . Учет этой особенности позволит экономнее использовать оперативную память компьютера и в конечном итоге ускорить вычисления.
Линейная алгебра
В предыдущем разделе мы рассмотрели общие принципы работы со специализированными пакетами Maple. Остановимся несколько подробнее на изучении одного из самых объемных (по числу функций) и часто используемых пакетов — linalg . (Отметим, что начиная с 6-й версии в комплект Maple входит еще один пакет по линейной алгебре — LinearAlgebra.)
Подгрузив пакет с помощью команды with, мы увидим перед собой перечень входящих в него функций, а также предупреждение о новом определении нормы и следа:
Warning, new definition for norm
Warning, new definition for trace
[BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp, QRdecomp, Wronskian, addcol, addrow, adj, adjoint, angle, augment, backsub, band, basis, bezout, blockmatrix, charmat, charpoly, cholesky, col, coldim, colspace, colspan, companion, concat, cond, copyinto, crossprod, curl, definite, delcols, delrows, det, diag, diverge, dotprod, eigenvals, eigenvalues, eigenvectors, eigenvects, entermatrix, equal, exponential, extend, ffgausselim, fibonacci, forwardsub, frobenius, gausselim, gaussjord, geneqns, genmatrix, grad, hadamard, hermite, hessian, hilbert, htranspose, ihermite, indexfunc, innerprod, intbasis, inverse, ismith, issimilar, iszero, jacobian, jordan, kernel, laplacian, leastsqrs, linsolve, matadd, matrix, minor, minpoly, mulcol, mulrow, multiply, norm, normalize, nullspace, orthog, permanent, pivot, potential, randmatrix, randvector, rank, ratform, row, rowdim, rowspace, rowspan, rref, scalarmul, singularvals, smith, stack, submatrix, subvector, sumbasis, swapcol, swaprow, sylvester, toeplitz, trace, transpose, vandermonde, vecpotent, vectdim, vector, wronskian]
Для знакомства с основными функциями пакета зададим несколько матриц, проиллюстрировав при этом различные способы их задания.
> F:=transpose(randmatrix(3, 3, unimodular, entries=rand(-3..3)));
В последнем случае мы сгенерировали верхнетреугольную унимодулярную матрицу (с указанием диапазона разброса коэффициентов) и затем транспонировали ее.
Найдем определитель матрицы C:
Для умножения согласованных матриц в Maple используется операция &* . Найдем разность произведений матриц A и B, взятых в противоположных порядках:
Мы видим, что вместо привычного для нас окончательного результата Maple вернул в качестве ответа некий «полуфабрикат» (умножение и вычитание матриц обозначены, но не выполнены). Дело в том, что для сложных объектов (матриц, массивов, таблиц, процедур) в Maple используется так называемое «правило вычисления до последнего имени» (last name evaluation). Это правило (в отличие от «правила вычисления до конца», используемого для менее громоздких объектов) применяется во избежание лишнего вывода на экран. Для того, чтобы все же вывести на экран интересующую нас матрицу, воспользуемся функцией evalm (другая возможность — использовать уже известную нам функцию op ):
Найдем ранг полученной матрицы:
Найдем матрицу, обратную к A. В этом случае, в отличие от бинарной операции умножения матриц, Maple вычисляет результат до конца:
Для матриц A и B найдем собственные значения и принадлежащие им собственные векторы:
Обратите внимание, что при обращении к функции eigenvectors (eigenvects) Maple возвращает собственные значения матрицы, их кратность как корней характеристического многочлена и базис подпространства из собственных векторов, принадлежащего каждому собственному значению.
Разумеется, Maple умеет работать не только с числовыми матрицами:
> f:=collect(charpoly(M, lambda), lambda);
В последнем примере мы нашли характеристический многочлен матрицы M и сгруппировали его относительно 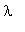
Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики
Источник