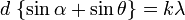Кольца ньютона вывести формулу для радиуса темного светлого кольца
Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании интерференционной картины не принимает. Поэтому мы ее и не будем учитывать.
При нормальном падении света кольца в отраженном свете имеют вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. Найдем радиусы темных колец (минимумов).
Сначала запишем условие образования темных колец. Они возникают там, где оптическая разность хода волн, отраженных от обеих поверхностей зазора, равна нечетному числу полуволн:
где связано с «потерей» полуволны при отражении от пластинки и . Отсюда
Далее, согласно теореме Пифагора (см. рис. 13), . Учитывая, что , получим
Из (37) и (38) следует, что радиус -го темного кольца
Заметим, что значению соответствует минимум темного пятна (не кольца). Аналогичный расчет можно провести и для светлых колец. Пример . Найдем радиус 5-го светлого кольца, если радиус кривизны выпуклой поверхности линзы и контакт ее с плоской поверхностью стекла идеальный (в точке). Длина волны света . Условие максимумов в данном случае имеет вид
где — толщина зазора в месте — го максимума (заметим, что если бы мы взяли , то значения надо было начинать с нуля). Согласно (38), . Из этих двух соотношений следует, что искомый радиус
Следует обратить внимание на то, что формула (39) справедлива лишь в случае идеального (точечного) контакта сферической поверхности линзы с пластинкой. Но идеальных контактов не бывает, номера колец не равны, вообщя говоря, порядку интерференции , и это обстоятельство необходимо учитывать при расчетах (см. задачу 5 из раздела 1.4 «Примеры решения задач»). Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру. С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей. Рассмотрим теперь на конкретном примере вопрос, связанный с причиной локализации колец Ньютона в очень малой области для обычных линз (кольца приходится рассматривать в микроскоп).
Пример . Плосковыпуклая линза, радиус кривизны сферической поверхности которой мм, соприкасается со стеклянной пластинкой. Оценим радиус наблюдаемой в отраженном свете интерференционной картины, если длина волны света и . Свет падает практически нормально. При нормальном падении света ограничивать интерференционную картину будет только длина когерентности . Кольца исчезают при условии , где — ширина зазора в месте исчезновения колец. Согласно (38), , а . Из этих формул получим , откуда
Число видимых колец равно . Этот результат можно получить и с помощью (39).
Источник
Кольца Ньютона в отражённом свете. Радиус светлых колец.
Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).
Радиус светлых колец Ньютона в отраженном свете:
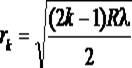
Вывод формулы смотреть в лекциях.
Кольца Ньютона в отражённом свете. Радиус тёмных колец.
Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).
Радиус темных колец Ньютона в отраженном свете:

Вывод формулы смотреть в лекциях.
Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля.
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.
Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.
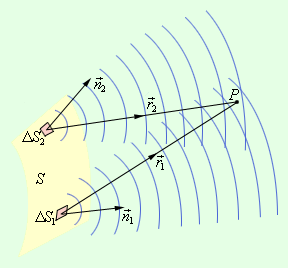 |
Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта,  и и 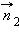 – нормали – нормали |
Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки Pдолжны отличается на половину длины волны, т. е.
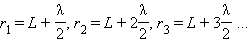 |
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности.
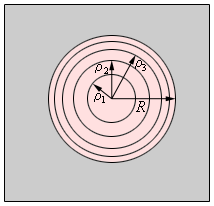 |
| Границы зон Френеля в плоскости отверстия |
Легко найти радиусы ρm зон Френеля:
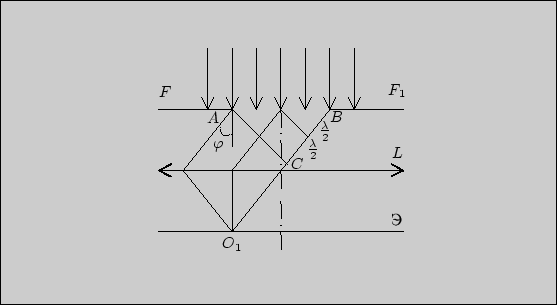
Дифракция на щели. При прохождении света через узкую щель за нею получаются дифракционные полосы. Кроме того, происходит интерференция отдельных лучей. В зависимости от наклона лучей к оси симметрии системы получаются неодинаковые разности хода — чередование светлых и темных полос
Дифракционная решётка. Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d. Если известно число штрихов ( Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид: Если же свет падает на решётку под углом Источник Кольца НьютонаПростая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона. Кольца НьютонаВозьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину, как было указано выше. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса. Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус. Все это вы можете проверить с помощью самостоятельных наблюдений. Но объяснить, почему возникают кольца Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе. Напротив, если вторая волна отстанет от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга. Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив, радиусы колец, можно вычислить длины волн. Кольца Ньютона в отражённом свете Длина световой волныДлина световой волны. Для красного света измерения дают λ = 8∙10 -7 м, а для фиолетового — λ = 4∙10 -7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы. Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому, как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны. Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10 -6 см) разница в длине световых волн. Интересно, что большинство животных не способны различать цвета. Они всегда видят черно-белую картину. При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся. Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в п раз. Так как v=λv, то при этом должна уменьшиться в п раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в п раз именно длина волны, а не частота. Источник |
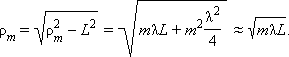
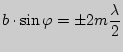
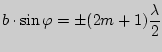

 ), приходящихся на 1 мм решётки, то период решётки находят по формуле:
), приходящихся на 1 мм решётки, то период решётки находят по формуле: 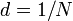 мм.
мм.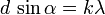
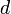 — период решётки,
— период решётки,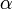 — угол максимума данного цвета,
— угол максимума данного цвета, — порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
— порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,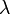 — длина волны.
— длина волны. , то:
, то: