Кто вывел 2 закон термодинамики

Необратимость тепловых процессов. Второй закон термодинамики. Понятие энтропии

Первый закон термодинамики – закон сохранения тепловых процессов, устанавливающий связь между количеством теплоты Q и изменением ∆ U внутренней энергии и работой А , совершенной над внешними телами:

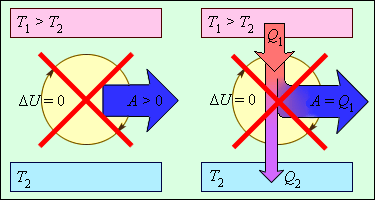
Исходя из закона, энергия не может быть создана или уничтожена: производится процесс передачи от одной системы к другой, принимая другую форму. Еще не было получено процессов, нарушающих первый закон термодинамики. Рисунок 3 . 12 . 1 показывает устройства, противоречащие первому закону.

Рисунок 3 . 12 . 1 . Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1 .

Обратимый и необратимый процессы

Первый закон термодинамики не устанавливает направления тепловых процессов. Опыты показывают, что большинство тепловых процессов протекают в одном направлении. Их называют необратимыми.

Если имеется тепловой контакт двух тел с разными температурами, тогда направление теплового потока направляется от теплого к холодному. Самопроизвольной передачи тепла от тела с низкой температуры к телу с высокой не наблюдается. Отсюда следует, что теплообмен с конечной разностью температур считается необратимым.

Обратимым процессом называется переход системы из одного равновесного расстояния в другое, которые возможно проводить в обратном направлении в той же последовательности промежуточных равновесных состояний. Она вместе с окружающими телами возвращаются к исходному состоянию.

Если система находится в состоянии равновесия во время процесса, она называется квазистатической.

Когда рабочее тело тепловой машины контактирует с тепловым резервуаром, температура которого неизменна во время всего процесса, то только изотермический квазистатический процесс считается обратимым, так как протекает с бесконечно малой разницей температур рабочего резервуара. Если имеется два резервуара, причем с разными температурами, тогда обратимым путем можно провести процессы на двух изотермических участках.

Так как адиабатический процесс проводится в обоих направлениях (сжатие и расширение), наличие кругового процесса с двумя изотермами и двумя адиабатами (цикл Карно) говорит о том, что это и есть единственный обратимый круговой процесс, где рабочее тело контактируется с двумя тепловыми резервуарами. Остальные при наличии 2 тепловых резервуаров считаются необратимыми.

Превращение механической работы во внутреннюю энергию считаются необратимыми при наличии силы трения, диффузии в газах и жидкостях, а процесс перемешивания по причине начальной разности давлений и так далее. Все реальные процессы считаются необратимыми, даже если значения будут максимально приближены к обратимым. Обратимые рассматриваются как пример реальных процессов.

Первый закон термодинамики не различает их. Правило требует от термодинамического процесса определенного энергетического баланса, но не говорит о том, возможен ли он. Установка направления прохождения процесса определяется вторым законом термодинамики. Его формулировка может звучать как запрет на определенные термодинамические процессы.

Второй закон был трактован У. Кельвином в 1851 .

В циклически действующей тепловой машине невозможно прохождение процесса, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.

Предположительно, машина с такими процессами могла бы получить название вечного двигателя второго рода.

При земных условиях могла бы быть отбита энергия Мирового океана и полностью превратилась бы в ее работу. Масса воды Мирового океана – 10 21 к г . Для его охлаждения хотя бы на 1 градус потребуется огромное количество энергии ≈ 10 24 Д ж , которое сравнимо с сжиганием 10 17 к г угля. Вырабатываемая энергия на Земле за год в 10 4 раз меньше. Отсюда и вывод о том, что вечный двигатель второго рода мало вероятен, как и двигатель первого, потому как оба они недопустимы, исходя из первого закона термодинамики.

Второй закон термодинамики

Формулировка 2 -го закона термодинамики была дана физиком Р. Клаузиусом.

Невозможно прохождение процесса, единственным результатом которого была бы передача энергии при помощи теплообмена от тела с низкой температуры к телу с более высокой.

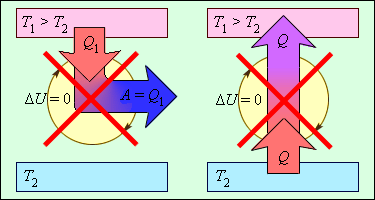
Рисунок 3 . 12 . 2 объясняет процессы, которые запрещены вторым законом, но разрешены согласно первому. Они соответствуют трактовкам второго закона термодинамики.

Рисунок 3 . 12 . 2 . Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – вечный двигатель второго рода; 2 – самопроизвольный переход тепла от холодного тела к более теплому (идеальная холодильная машина).

Формулировки обоих законов считаются эквивалентными.

Когда тело без помощи внешних сил переходит при теплообмене от холодного к горячему, то возникает мысль о возможности создания вечного двигателя второго рода. Если такая машина получит количество теплоты Q 1 от нагревателя и отдаст холодильнику Q 2 , тогда совершается работа A = Q 1 — Q 2 . Если бы Q 2 самопроизвольно перешло к нагревателю, то конечный результат тепловой машины и идеальной холодильной машины выглядело бы таким образом Q 1 — Q 2 . Причем сам переход происходил бы без изменений холодильника. Отсюда вывод – комбинация тепловой машины и идеальной холодильной машины равноценна двигателю второго рода.

Прослеживается связь между вторым законом термодинамики и необратимостью реальных тепловых процессов. Энергия теплового движения молекул отлична от механической, электрической и так далее. Она способна превратиться в другой вид энергии только частично. Поэтому при наличии энергии теплового движения молекул любой процесс считается необратимым, так как полностью в обратном направлении он не осуществим.

Свойство, относящееся к необратимым процессам, говорит о том, что они проходят в термодинамически неравновесной системе, а результат получается в виде замкнутой системы, приближающейся к состоянию термодинамического равновесия.

Теоремы Карно

Имеются теоремы Карно, которые могут быть доказаны, исходя из второго закона термодинамики.

КПД тепловой машины, работающей при данных значениях температур нагревателя холодильника, не может иметь значение больше, чем КПД действия машины, работающей согласно обратимому циклу Карно с теми же значениями температур нагревателя и холодильника.

КПД действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.

Отсюда следует, что КПД действия машины с циклом Карно считается максимальным.

η = 1 — Q 2 Q 1 ≤ η m a x = η К а р н ю = 1 — T 2 T 1 .

Знак равенства данной записи говорит об обратимости процесса. Если машина работает по циклу Карно, тогда:

Q 2 Q 1 = T 2 T 1 или Q 2 T 2 = Q 1 T 1 .

Знаки Q 1 и Q 2 всегда отличаются независимо от направления цикла. Поэтому получаем:

Q 1 T 1 + Q 2 T 2 = 0 .

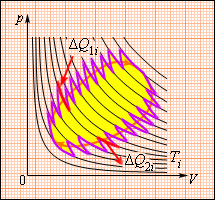
Рисунок 3 . 12 . 3 говорит о том, что данное соотношение обобщается и представляется в виде последовательности малых изометрических и адиабатических участков.

Рисунок 3 . 12 . 3 . Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.

Полный обход замкнутого обратимого цикла имеет вид:

∑ ∆ Q i T i = 0 (обратимый цикл).

Откуда ∆ Q i = ∆ Q 1 i + ∆ Q 2 i – количество теплоты, полученное рабочим телом на двух изотермических участках с температурой T i . Чтобы данный цикл провести наоборот, нужно рабочее тело сконтактировать со многими тепловыми резервуарами с T i .

Энтропия

Отношение Q i T i получило название приведенного тепла. Формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Благодаря ей вводится еще одно понятие – энтропия, обозначаемая S . Ее открыл Р. Клаузиус в 1865 году.

При переходе из одного равновесного состояние в другое изменяется и ее энтропия. Разность энтропий двух состояний равняется приведенному теплу, полученному системой во время обратного перехода состояния.

∆ S = S 2 — S 1 = ∑ ( 1 ) ( 2 ) ∆ Q i о б р T .

Если рассматривается адиабатический процесс ∆ Q i = 0 , тогда энтропия S не изменяется.

Изменение энтропии ∆ S во время перехода в другое состояние фиксируется как формула:

∆ S = ∫ ( 1 ) ( 2 ) d Q о б р T .

Определение энтропии достаточно точное. Разность ∆ S двух состояний системы подразумевает физический смысл. Если имеется необратимый переход, а необходимо найти энтропию, тогда нужно придумать обратимый процесс, который свяжет начальное и конечное состояние. После этого перейти к нахождению приведенного тепла, полученного системой.

Рисунок 3 . 12 . 4 Модель энтропии и фазовых переходов.

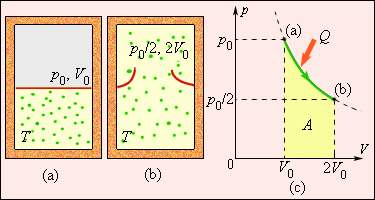
Рисунок 3 . 12 . 5 показывает необратимый процесс расширения шага с отсутствием теплообмена. Равновесными считаются начальное и конечное значение, изображаемые на диаграмме p , V . Точки a и b соответствуют состояниям и располагаются на одной изотерме. Чтобы найти ∆ S , следует перейти к рассмотрению обратимого изотермического перехода из a в b . При изопроцессе газ получает определенное количество теплоты окружающих тел Q > 0 , тогда при необратимом расширении энтропия возрастет до ∆ S > 0 .

Рисунок 3 . 12 . 5 . Расширение газа в «пустоту». Изменение энтропии ∆ S = Q T = A T > 0 где A = Q – работа газа при обратимом изотермическом расширении.

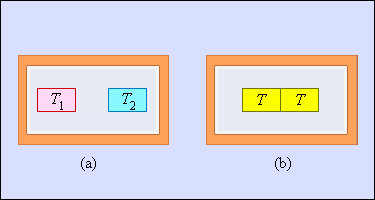
Еще одним примером необратимого процесса считается теплообмен при конечной разности температур. Рисунок 3 . 12 . 6 и показывает два тела, заключенные в адиабатическую оболочку, где начальные температуры обозначаются как T 1 и T 2 T 1 . Течение процесса теплообмена способствует выравниванию температур. Очевидно, что теплое тело отдает, а холодное принимает. Холодное тело превосходит по модулю приведенное тепло, отдаваемое горячим. Отсюда вывод – изменение энтропии в замкнутой системе необратимого процесса ∆ S > 0 .

Рисунок 3 . 12 . 6 . Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии Δ S > 0 .

Все самопроизвольно протекающие процессы в изолированных термодинамических процессах характеризуются ростом энтропии.

Обратимые процессы имеют постоянную энтропию ∆ S ≥ 0 . Соотношение называют законом возрастания энтропии.

При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо не меняется, либо возрастает.

Наличие энтропии говорит о самопроизвольно протекающем процессе, а ее рост – приближение всей системы к термодинамическому равновесию, где S принимает максимальное значение. Возрастание энтропии можно трактовать как формулировку второго закона термодинамики.

В 1878 году Л. Больцман дал вероятностное определение понятию энтропии, так как было предложено рассматривать ее в качестве меры статистического беспорядка замкнутой термодинамической системы. Все самопроизвольно протекающие процессы в таких системах приближают ее к равновесному состоянию, так как сопровождаются ростом энтропии, и направляют в сторону увеличения вероятности состояния.

Если состояние макроскопической системы содержит большое число частиц, то его реализация может предусматривать несколько способов.

Термодинамическая вероятность W системы – это количество способов, которыми реализуется данное состояние макроскопической системы, макросостояний, осуществляющих его.

Из определения имеем, что W ≫ 1 .

При наличии 1 м о л ь газа в емкости существует число N способов размещения молекулы по двум половинам емкости: N = 2 N А , где N А — число Авогадро. Каждое из них – это микросостояние.

Одно из них соответствует случаю с молекулами, собранными в одной половине сосуда. Вероятность такого события приравнивается к нулю. Большое количество состояний соответствует такому, где молекулы распределяются равномерно по всей площади емкости.

Тогда равновесное состояние является наиболее вероятным.

Равновесное состояние считается состоянием наибольшего беспорядка в термодинамической системе с максимальной энтропией.

Исходя из трактовок Больцмана, энтропия S и термодинамическая вероятность W связаны:

S = k · ln W , где k = 1 , 38 · 10 — 23 Д ж / К является постоянная Больцмана. Отсюда следует, что определение энтропии определяется логарифмом числа микросостояний. Именно они способствуют реализации данного макросостояния. Тогда энтропия может быть рассмотрена в качестве меры вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Их называют флуктуациями.

В системах с большим числом частиц отклонения от состояния равновесия имеют достаточно малую вероятность на существование.

Источник

Второе начало термодинамики: вечный двигатель второго рода и тепловая смерть Вселенной

• 12 января 2021 г.
• 14 минут
• 13 981

Пришла пора разобраться со вторым фундаментальным постулатом термодинамики, который именуется второе начало термодинамики. Второе начало не является доказуемым в рамках классической термодинамики. Его формулировки – результат обобщения опытов, наблюдений и экспериментов. Попытаемся рассказать о нем кратко и понятно.

В прошлой статье по термодинамике мы говорили о термодинамических системах, состоящих из большого числа частиц. Для описания подобных систем используются так называемые функции состояния.

Термодинамическая функция состояния (или термодинамический потенциал) – это функция, зависящая от нескольких независимых параметров, определяющих состояние системы. Чтобы было понятнее, приведем пример. Одна из функций состояния системы – это ее внутренняя энергия. Она не зависит от того, как именно система оказалось в данном состоянии

Энтропия

Еще одно понятие, с которым нужно познакомиться – это энтропия. Для понимания второго начала термодинамики энтропия очень важна. А еще это красивое слово, которое многих ставит в ступор и которым можно блеснуть в компании.

В самом общем случае, энтропия – мера хаотичности некоторой системы

Энтропия

Простой пример : представим, что у вас есть ящик с носками. Если все носки в ящике разбросаны и валяются вперемешку и по одному, энтропия такой системы максимальна. А если носки собраны по парам и лежат аккуратненько в рядок — минимальна.

В термодинамике, энтропия – это функция состояния термодинамической системы, которая определяет меру необратимого рассеивания энергии. Что это значит? Это значит, что какая-то часть внутренней энергии системы не может перейти в совершаемую системой механическую работу. Например, процесс преобразования теплоты в механическую работу всегда сопровождается потерями, в результате которых теплота трансформируется в другие виды энергии.

Энтропия при необратимых термодинамических процессах увеличивается, а при обратимых – остается постоянной. Математическая запись энтропии (S):

Здесь дельта Q – количество теплоты, подведенное или отведенное от системы, T – температура системы, dS – изменение энтропии.

Существует несколько различных формулировок второго начала термодинамики, и вот одна из них:

Энтропия замкнутой системы возрастает при любых необратимых процессах в этой системе

Так как нас интересует именно понимание сути вещей, приведем еще одно самое простое определение:

Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему

К слову, данная формулировка второго начала термодинамики принадлежит Рудольфу Клаузиусу, который и ввел в обиход понятие энтропии.

Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему

И снова вечный двигатель

После разочарования с идеей вечного двигателя первого рода люди и не думали сдаваться. Через какое-то время был придуман вечный двигатель второго рода, работа которого основывалась на передаче тепла и не перечила закону сохранения энергии. Такой двигатель преобразует все тепло, полученное от окружающих тел, в работу. Например, в качестве его реализации предполагалось путем охлаждения океана получить огромное количество теплоты. Но к счастью до охлаждения океана и заморозки рыб дело не дошло, т.к. данная идея противоречит второму началу динамики. КПД любой машины не может быть равен единице, также как тепло не может быть преобразовано в работу полностью. Так что сколько ни старайтесь, а вечный двигатель второго рода создать невозможно, так же как и вечный двигатель первого рода.

Тепловая смерть Вселенной

После введения Рудольфом Клаузиусом понятия энтропии в 1865 году возникло множество споров, домыслов и теорий, связанных с этим понятием. Одна из них – гипотеза о тепловой смерти Вселенной, сформулированная самим Клаузиусом на основе второго начала термодинамики.

Рудольф Клаузиус (1822-1888)

Данная теория, сформулированная Клаузиусом, гласит, что Вселенная, как любая замкнутая система, стремится к состоянию термодинамического равновесия, характеризующемуся максимальной энтропией и полным отсутствием макроскопических процессов, что в свою очередь обессмысливает привычное нам понятие времени. По Клаузиусу: «Энергия мира остается постоянной. Энтропия мира стремиться к максимуму». Это означает, что когда Вселенная придет в состояние термодинамического равновесия, все процессы прекратятся и мир погрузиться в состояние «тепловой смерти». Температура в любой точке Вселенной будет одной и той же, более не будет каких-либо причин, способных вызвать возникновение каких бы то ни было процессов.

Концепция тепловой смерти вселенной еще в недалеком прошлом была довольно широко распространена и являлась предметом активных дискуссий. Так, в книге Джинса «Universe around us» (1932г.) можно найти следующие строки касательно тепловой смерти Вселенной: «Вселенная не может существовать вечно; рано или поздно должно наступить время, когда ее последний эрг энергии достигнет наивысшей степени на лестнице падающей полезности, и в этот момент активная жизнь Вселенной должна будет прекратиться».

Где-то во Вселенной

При выводе своей теории Клаузиус прибегал в своих рассуждениях к следующим экстраполяциям (приближениям):

1. Вселенная рассматривается как замкнутая система.
2. Эволюция мира может быть описана как смена его состояний.

Интересный факт : рассуждения о тепловой смерти позволили церкви заявить, что с научной точки зрения (в том числе и благодаря теории Клаузиуса) можно найти предпосылки, указывающие на существование бога. Так, в 1952 году на заседании «папской академии наук» папа Пий 12-й в своей речи сказал: «Закон энтропии, открытый Рудольфом Клаузиусом, дал нам уверенность, что спонтанные природные процессы всегда связаны с некоторой потерей свободной, могущей быть использованной энергии, откуда следует, что в замкнутой материальной системе в конце концов эти процессы в макроскопическом масштабе когда-то прекратятся. Эта печальная необходимость. красноречиво свидетельствует о существовании Необходимого Существа».

Опровержение теории тепловой смерти Вселенной

Как уже отмечалось выше Клаузиусом, при выводе его теории применялись определенные экстраполяции. Сегодня несмотря на некоторые сложности можно с уверенностью сказать, что подобные выводы являются антинаучными. Дело в том, что существуют определенные границы применимости второго начала термодинамики: нижняя и верхняя. Так, второе начало термодинамики не может быть применено для описания микросистем, размеры которых сравнимы с размерами молекул, и для макросистем, состоящих из бесконечного числа частиц, т.е. для Вселенной в целом.

Второе начало термодинамики не применимо ко Вселенной как замкнутой системе

Собственно первым ученым, установившим статистическую природу второго начала термодинамики и противопоставившим теории тепловой смерти Вселенной так называемую флуктуационную гипотезу, был выдающийся физик-материалист Больцман. Имеет место формула Больцмана, позволяющая дать статистическое истолкование второму началу термодинамики

Здесь S – энтропия системы, k – постоянная Больцмана, P – термодинамическая вероятность состояния, определяющая число микросостояний системы, соответствующих данному макросостоянию. Согласно формуле Больцмана,

То есть термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать. Однако т.к. для систем, состоящих из бесконечного числа частиц, все состояния будут равновероятными , вышеописанное соотношение неприменимо ко Вселенной. В подобных системах имеют место значительные флуктуации (флуктуация – отклонение истинного значения некоторой величины от ее среднего значения), представляющие собой отклонения от второго начала термодинамики. Согласно Больцману, состояние термодинамического равновесия представляет собой лишь наиболее часто встречающееся и наиболее вероятное; наряду с этим в равновесной системе могут самопроизвольно возникнуть сколь угодно большие флуктуации. То есть во Вселенной, находящейся в состоянии термодинамического равновесия, постоянно возникают флуктуации, причем одной такой флуктуацией является та область пространства, в которой находимся мы.

Людвиг Больцман (1844-1906)

Современный подход безусловно отвергает теорию тепловой смерти Вселенной. Учитывая огромный возраст Вселенной и тот факт, что она не находится в состояние тепловой смерти, можно сделать вывод о том, что во Вселенной протекают процессы, препятствующие росту энтропии, т.е. процессы с отрицательной энтропией. Однако выводам Больцмана о том, что во Вселенной преобладает состояние термодинамического равновесия, все более противоречит растущий экспериментальный материал астрономии. Материя обладает никогда не утрачиваемой способностью к концентрации энергии и превращения одних форм движения в другие. Так, например, процесс образования из рассеянной материи звезд подчиняется определенным закономерностям и не может быть сведен исключительно к случайным флуктуациям распределения энергии во Вселенной.

Дорогие друзья! Сегодня мы по возможности выяснили, какой смысл имеет понятие энтропии для второго начала термодинамики, узнали, что вечный двигатель второго рода невозможен, а также порадовались, что тепловой смерти Вселенной все-таки не случится. Мы как всегда надеемся на то, что вам понравилась наша статья, в которой мы старались рассказать о термодинамике просто, понятно и интересно. Желаем успехов в учебе и напоминаем – подсказать, помочь, проконсультировать и взять часть нагрузки на себя всегда готовы наши специалисты. Учитесь и живите в свое удовольствие!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник