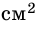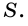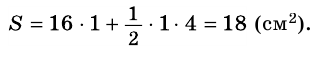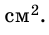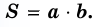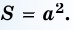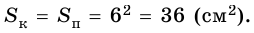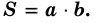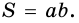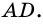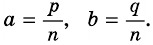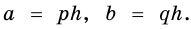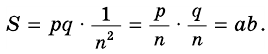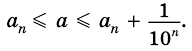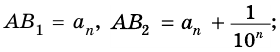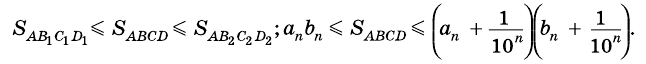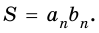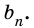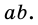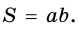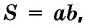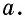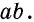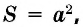- Кто вывел формулу площади прямоугольника
- Содержание
- Что такое площадь и что такое прямоугольник
- Как найти площадь прямоугольника
- Зачем уметь находить площадь
- Единицы измерения площади
- Задачи и упражнения
- Вопросы и задания
- Историческая справка
- Площадь прямоугольника — определение и вычисление с примерами решения
- Определение площади прямоугольника
- Теорема о площади прямоугольника
- Площадь прямоугольника с доказательством
Кто вывел формулу площади прямоугольника
Площадь. Формула площади прямоугольника
Содержание
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры.
На протяжении многих веков так повелось, что вычисление площади называли квадратурой. То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.
Поэтому, можно подвести итог, что площадь – это такая величина, которая показывает нам размер части плоскости, соединенной между собой отрезками.
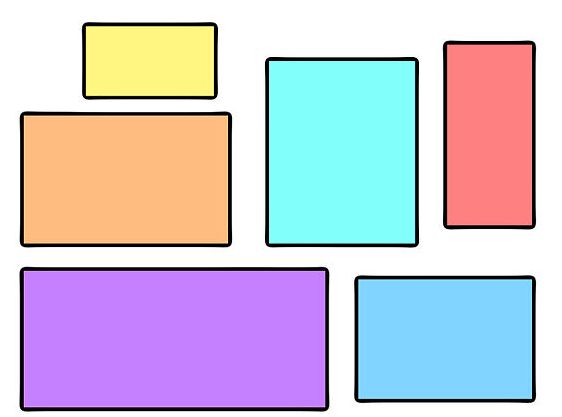
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть, четырехстороннюю фигуру, которая имеет четыре прямых угла и ее противоположные стороны равны, называют прямоугольником.
Как найти площадь прямоугольника
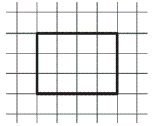
Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв. см.
Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.
А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.
В итоге получаем вот такую формулу:
Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.
Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.
Зачем уметь находить площадь
• Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
• Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
• В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.
То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:
Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.
А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника? Какая разница между площадью и периметром
Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Единицы измерения площади
Если периметр одномерный измеряется в линейных единицах, которыми являются дюймы, футы и метры, то S относится к двумерным исчислениям и имеет свою длину и ширину.
И измеряется S в квадратных единицах, таких, как:
• Один квадратный миллиметр, где S квадрата имеет сторону, равную одному миллиметру;
• Квадратный сантиметр, имеет S такого квадрата, у которого сторона равна одному сантиметру;
• Квадратный дециметр равен S этого квадрата со стороной в один дециметр;
• Квадратный метр имеет S квадрата, сторона которого равна одному метру;
• И наконец, квадратный километр имеет S квадрата, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли используют такие единицы, как:
• Один ар или сотка – если S квадрата имеет сторону десять метров;
• Один гектар равен S квадрата, у которого сторона имеет сто метров.
Задачи и упражнения
А теперь давайте рассмотрим несколько примеров.
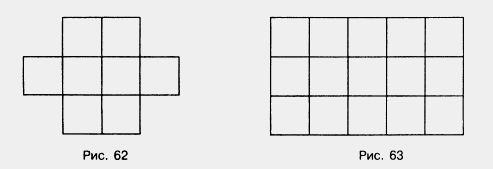
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.
Если записать, то это будет выглядеть так:
1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:
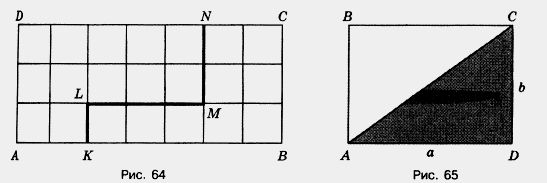
Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2. Теперь давайте найдем площадь всего прямоугольника:
Итак, берем три и умножаем на семь и получаем 21 кв.см:
3 • 7 = 21 кв.см. При этом 21 = 12 + 9.
И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.
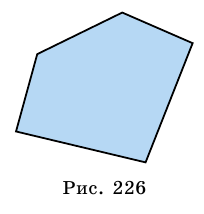
Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC
А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.
Представим, что сторона квадрата равна а, то:
Делаем вывод, что формула площади квадрата будет иметь такой вид:
А запись a2 называется квадратом числа а.
И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 • 4, то есть 4 * 2 = 16 кв.см.
Вопросы и задания
• Найдите площадь фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
• Вспомните формулу прямоугольника и запишите ее.
• Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
• Дайте определение равным фигурам.
• Могут ли иметь равные фигуры различные площади? А периметры?
• Если вам известны площади отдельных частей фигуры, как узнать ее общую площадь?
• Сформулируйте и запишите, чему равняется площадь квадрата.
Историческая справка
А известно ли вам, что древние люди в Вавилоне умели рассчитать площадь прямоугольника. Так же древние египтяне делали расчеты различных фигур, но так как точных формул они не знали, то вычисления имели небольшие погрешности.
В своей книге «Начала» знаменитый древнегреческий математик Евклид, описывает различные способы вычисления площадей разных геометрических фигур.
Источник
Площадь прямоугольника — определение и вычисление с примерами решения
Содержание:
Любой многоугольник ограничивает некоторую часть плоскости. Эту часть плоскости называют внутренней областью многоугольника. На рисунке 226 внутренняя область многоугольника закрашена. Будем рассматривать многоугольник вместе с его внутренней областью.
Определение площади прямоугольника
Каждому многоугольнику можно поставить в соответствие значение его площади, считая, что площадь многоугольника — это та часть плоскости, которую занимает многоугольник. Понятие площади нам известно из повседневной жизни (площадь комнаты, площадь огорода, площадь страницы). С понятием площади вы также знакомились на уроках математики в 5-6-х классах.
Сформулируем основные свойства площади:
- площадь каждого многоугольника является положительным числом;
- равные многоугольники имеют равные площади;
- если многоугольник разбит на несколько многоугольников, то его площадь равна сумме площадей этих многоугольников;
- единицей измерения площади является площадь квадрата со стороной, равной единице измерения длины (такой квадрат еще называют единичным квадратом).
Например, если за единицу измерения длины взять 1 см, то соответствующей единицей измерения площади будет площадь квадрата со стороной 1 см. Такой квадрат имеет площадь 1
Площадь фигуры принято обозначать буквой
Пример:
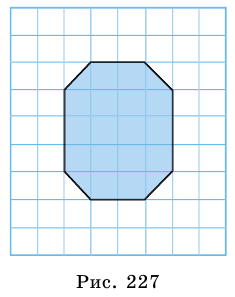
Найдите площадь многоугольника, изображенного на рисунке 227, если сторона клетки равна 1 см.
Решение:
Внутренняя область многоугольника состоит из шестнадцати клеток со стороной 1 см, площадь каждой из которых 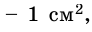
Ответ. 18
Площади некоторых фигур можно находить по формулам. Например, из курса математики предыдущих классов нам известны формулы для вычисления площадей прямоугольника, квадрата, круга.
Теорема (о площади прямоугольника). Площадь 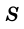
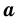
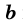
Доказательство этой теоремы достаточно громоздко, ознакомиться с ним можно в Приложении 2 (с. 194).
Если стороны прямоугольника 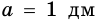
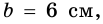
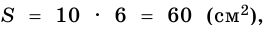
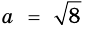
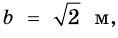
Следствие. Площадь 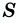
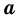
Пример:
Квадрат и прямоугольник имеют равные площади. Сторона квадрата равна 6 см, а одна из сторон прямоугольника в 4 раза больше другой. Найдите периметр прямоугольника.
Решение:
Пусть 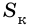
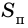
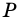
1)
2) Пусть одна из сторон прямоугольника равна 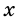
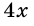
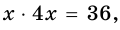
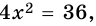
Учитывая, что 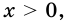
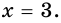
3) 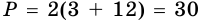
Геометрические знания, связанные с измерением площади, берут свое начало в глубине тысячелетий.
Еще за 2-3 тысячи лет до н. э. вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Эталоном при измерении площадей им служил квадрат со стороной, равной единице длины.
Древние египтяне 4000 лет назад для измерения площади прямоугольника, треугольника и трапеции уже пользовались теми же формулами, что и мы сейчас.
В своих «Началах» Евклид не употреблял слово «площадь», так как он уже под самим словом «фигура» понимал часть плоскости, ограниченную той или иной замкнутой линей, т. е. площадь. Евклид не выражал результат измерения площади числом, а сравнивал площади разных фигур между собой, употребляя слово «равновеликие». Как, например, в Задаче 16 из первой книги «Начал»: «Параллелограммы, находящиеся на равных основаниях и между теми же параллельными, равны между собой, т. е. равновелики. Докажите!».
Как и другие ученые древности, Евклид занимался вопросами превращения одних фигур в другие, им равновеликие. Так, в «Началах» решалась задача о построении квадрата, равновеликого любому данному многоугольнику.
Теорема о площади прямоугольника
Теорема (о площади прямоугольника). Площадь 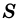
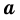
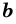
Доказательство:
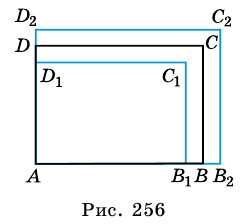
Пусть 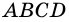
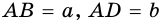
1) Если длины отрезков 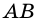
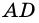
(целыми или дробными), то существует отрезок такой длины 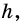
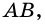
Приведем числа 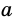
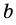
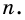
Тогда 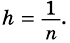
Разобьем отрезок 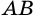
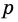
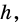
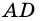
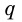
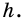
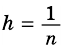
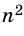
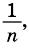
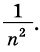
2) Рассмотрим случай, когда хоть одна из длин отрезков 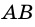
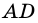
Пусть число 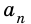
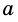
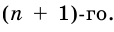
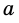
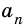
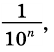
Аналогично рассмотрим число 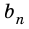
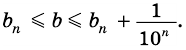
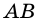
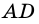
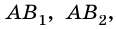
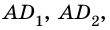
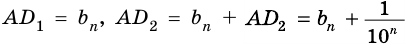
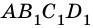
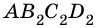
Будем неограниченно увеличивать число 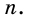
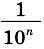
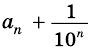
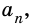
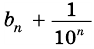
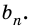
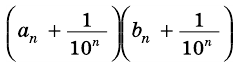
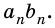
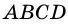
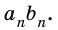
Но из неравенств 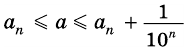
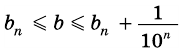
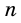
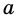

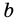
Следовательно, число 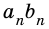
Окончательно имеем:
Площадь прямоугольника с доказательством
Самой простой фигурой с точки зрения вычисления площади является прямоугольник.
Теорема (формула площади прямоугольника)
Площадь прямоугольника равна произведению его соседних сторон:
где 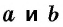
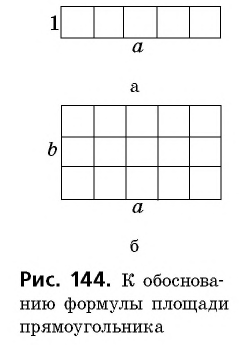
Приведем рассуждения, на которых основывается доказательство этой теоремы.
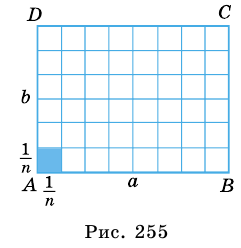
Сначала необходимо рассмотреть прямоугольник со сторонами 1 и 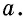
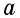
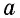
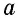
В общем случае для прямоугольника со сторонами 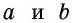
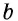
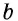
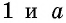
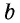
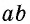
Полное доказательство этой теоремы приводится в Приложении 1.
Следствие (формула площади квадрата)
Площадь квадрата равна квадрату его стороны:
где 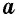
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Многоугольник
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник