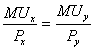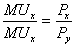Дополнения



Условия и формула потребительского равновесия
Существует тесная взаимосвязь между количеством товара, его предельной полезностью и ценой. Она состоит в том, что чем больше товара, тем относительно меньше стремление потребителя приобретать его последнюю единицу. Избыточное количество товаров значительно снижает их предельную полезность, и соответственно этому падают цены. Если воспользоваться принятыми обозначениями предельной полезности и цены, то эту зависимость можно выразить математически
| MUА /РА = MUВ / РВ = MUС / РС = MUZ / РZ = l, |
где l — величина, характеризующая предельную полезность на единицу денежных затрат бюджета.
Каждое из приведенных в данной формуле отношений, например MUА /РА или MUВ / РВ означает прирост общей полезности в результате увеличения расходов потребителя на товар А или товар В на один рубль. Каждое отдельно взятое отношение данной формулы расценивается как предельная полезность, приходящаяся на один рубль. Данное условие максимизации полезности потребителем можно представить в другой пропорции, переставив члены исходных отношений: MUА / MUВ = РА / РВ. Это уравнение означает, что отношение предельных полезностей двух товаров должно равняться отношению цен этих товаров. Оно также указывает на то, что равновесие потребителя устанавливается при условии, что он тратит доход так, что предельная полезность на каждую потраченную денежную единицу устанавливается по любому купленному товару. При отсутствии равенства потребитель может максимизировать полезность в пределах тех же затрат, но перераспределяя их в пользу того товара, у которого предельная полезность выше.
Если все отношения в любом наборе товаров и услуг равны между собой и их можно представить в виде вышеприведенной формулы, то в таких случаях говорят о равновесии потребителя, или потребительском равновесии. Суть потребительского равновесия состоит в том, что предельная полезность, получаемая в расчете на рубль, потраченный на один товар, равна предельной полезности, получаемой на рубль, потраченный на другой товар. В состоянии равновесия потребитель не склонен к каким бы то ни было переменам в структуре расходов.
Рациональный человек, совершая тот или иной выбор, не всегда с полной определенностью знает его последствия. Это относится и к потребительскому выбору. Вы приобрели фарфоровую чашку и желаете насладиться ее красотой, но назавтра после покупки случайно поставили ее мимо стола, и покупка оказалась “менее полезной”, чем вы рассчитывали.
Или вы купили арбуз, и он оказался гораздо вкуснее, чем можно было подумать по его виду. Но все могло случиться по-иному: чашка могла бы служить вам много лет и ее ценность повышалась бы, а арбуз мог оказаться невкусным. Полезность покупки могла оказаться той или иной и из-за изменения условий ее использования (классический пример в новелле О’Генри “Дары волхвов”). Помимо этих эпизодов человек сознательно совершает ряд действий, результаты которых носят случайный характер. Он участвует в лотереях и играет в азартные игры. Он страхует свою жизнь и свое имущество, регулярно внося страховую плату и надеясь, что с ним не произойдет “страховой случай”, но не исключая такой возможности. Теория игр, созданная в 20-е гг. одним из самых блестящих ученых XX в. Джоном фон Нейманом, рассматривала поведение “игрока” в условиях, когда последствия его “хода” полностью не определяются его выбором. Более того, оказалось, что игрок, стремящийся к максимальному выигрышу, при определенных условиях должен делать случайные ходы. Теория игр породила новые подходы к анализу поведения экономического субъекта. Основные теоретические результаты в этом направлении были изложены Джоном фон Нейманом и Оскаром Моргенштерном в фундаментальном труде “Теория игр и экономическое поведение”, вышедшем в свет в 1943 г. (в русском переводе в 1970 г.).
Основное допущение, принятое Дж. фон Нейманом и О. Моргенштерном, состоит в том, что потребитель и в случайных ситуациях ведет себя рационально. А это значит, что, производя свой выбор, он сопоставляет не только варианты с однозначными исходами, но и такие варианты, исходы которых имеют случайную полезность. В последнем случае потребитель должен знать как все возможные исходы, так и их вероятности.

Оказалось, что в таком допущении содержится все необходимое для существования количественной меры полезности.
Авторы приводят такой пример. Некто предпочитает стакан чая (Ч) чашке кофе (К), а чашку кофе — стакану молока (М). Допустим, что он поставлен перед выбором: чашка кофе или стакан с неизвестным содержимым, которое с равными вероятностями может оказаться чаем и молоком. Если субъект выбрал кофе, это значит, что из двух предпочтений (Ч > К) и (К > М) второе оказалось более значимым. Следовательно, по своей полезности кофе ближе к чаю, чем к молоку. Если бы он выбрал стакан с неизвестным содержимым, это позволило бы сделать противоположный вывод. Если, наконец, ему безразлично, какую из двух возможностей выбрать, то это означает, что оба предпочтения, Ч > К и К > М, для него равноценны и полезность чашки кофе находится ровно посредине между полезностями стакана чая и стакана молока. Как мы уже видели, возможность сравнивать пары благ или их наборов — это уже основание для построения количественной шкалы полезностей.
Имея дело со случайными последствиями решений и, используя для их оценки математические ожидания полезностей, мы не можем выбирать для измерения полезностей шкалы, согласованные друг с другом только в отношении порядка. Какая-то из рассмотренных нами шкал, а может быть, и обе, не годятся для представления случайных полезностей. Дж. фон Нейман и О. Моргенштерн разработали систему аксиом количественной полезности. Из этих аксиом следует существование такой функции полезности, математическое ожидание значений которой согласовано с предпочтениями субъекта.
А раз такая функция существует, можно представить себе инструмент для измерения ее значений. Всякое измерение есть сравнение с эталоном. В нашем случае в качестве эталона следовало бы выбрать такую вещь, приобретение которой вело бы к случайным результатам, сильно различающимся по полезности. Идеальным примером подобной вещи служит лотерейный билет: покупатель, изучив условия лотереи, знает, какие в ней разыгрываются призы и может оценить вероятность получения каждого из них. Единственное чего он не знает, достанется ли ему выигрыш.
Источник
Учебные материалы
Модель поведения потребителя предполагает, что покупатель стремится получить наивысший уровень полезности, т.е. максимизирует полезность при наличном бюджетном ограничении.
Для определения максимального уровня удовлетворения потребностей потребителя необходимо совместить бюджетную линию и карту кривых безразличия на одном графике. Мы практически совмещаем потребности потребителя и его возможности.
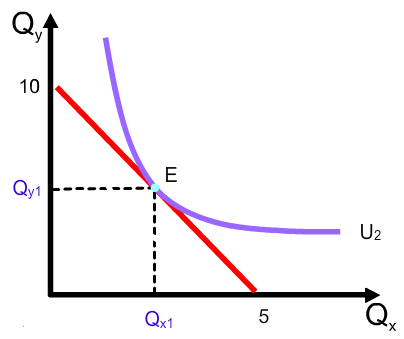
Максимизация достигается в точке, в которой бюджетная линия является касательной к кривой безразличия.
Эта точка является точкой потребительского равновесия.
На рис. 6.9 мы используем модель, чтобы определить выбор потребителя относительно недельного потребления апельсинов и яблок в рамках своего бюджетного ограничения.
Максимальная полезность, достигаемая при данном бюджете, обеспечивается набором в точке Е с координатами Qх1, Qу1. Это и есть выбранный потребительский набор. Ни одна из других комбинаций не доставит потребителю большей полезности при данном доходе.
Равновесие потребителя соответствует такой комбинации покупаемых товаров, которые максимизируют полезность приданном бюджетном ограничении. Это есть равновесие в том смысле, что при известных предпосылках модели, как только потребитель получает такой набор, у него нет больше стимула менять его на другой.
Можно показать равновесие потребителя с помощью предельной полезности, исходя из предположения, что ее можно количественно измерить. Каждый потребитель стремится повысить свою общую полезность, а значит использовать и распределить доход так, чтобы предельная полезность от израсходованной денежной единицы на тот или иной товар была одинаковой.
Общее условие равновесия потребителя (принцип равной полезности) указывает, что потребитель в равновесии распределяет расходы на все товары таким образом, что их предельные полезности в расчете на доллар (рубль, франк и т.д.) должны быть равными.
Если МUx – предельная полезность товара X, МUy – предельная полезность товара Y, Рx – цена товара X, Рy – цена товара Y, то вышесказанное можно определить формулой:
Например, если предельная полезность товара Х (скажем корзина яблок) равна 100, а его цена 10 долл., предельная полезность товара Y (скажем корзина апельсинов) – 50, а его цена 5 долл., то предельная полезность на доллар будет в обоих случаях равна 10. Это уравнение показывает, что при этих условиях потребитель не может переместить ни цента на другой товар и повышать его полезность.
Данное уравнение можно преобразовать:
Это уравнение отражает установление равновесия, когда потребитель сделал все возможное, чтобы максимизировать свой выбор, свою полезность. Ведь когда он приходит на рынок, то сталкивается с огромным количеством цен, ему приходится регулировать свой выбор, отдавать предпочтение товарам таким образом, чтобы их предельная полезность на один доллар (на одну денежную единицу) были равны.
Например, как потратить 4 доллара в буфете, где потребителю предлагают лишь два товара: пирожное по цене 2 долл. за штуку и сок по цене 1 долл. за стакан (таблица 6.4).
Таблица 6.4 – Принцип максимизации полезности, усл.ед.
Источник
V3: Теория поведения потребителя.
I: k = A
S:Предположим, что кривая производственных возможностей страны задаётся уравнением х²+у²=4500, где х,у- производимые блага. Каким будет оптимальный набор производства этих благ, если функция полезности задана уравнением u=2х+у:
I: k = A
S:Кем было введено в научный оборот понятие полезности:
I: k = A
S:Полезность товара для потребителя носит:
-: правильного варианта нет
I: k = В
S:Кто ставит задачу выявить предпочтение потребителей путем соизмерения и сопоставлении полезностей благ:
I: k = B
S:Предельная полезность:
-: прямо пропорциональная объему потребляемых товаров
+: обратно пропорциональная объему потребляемых товаров
+: определяется путем деления разности общих полезностей на изменение количества товара
-: определяется путем деления суммы общих полезностей на изменение количества товара
I: k = C
S:Величина предельной полезности составляет 3, изменение количества равно 12. Изменение общей полезности составит:
I: k = В
S:Распределите в порядке уменьшения предпочтительности товара для потребителя при следующих условиях. Товар А: предельная полезность-10, цена-1. Товар B: предельная полезность-10, цена-2. Товар C: предельная полезность-10, цена-3. Товар D: предельная полезность-10, цена- 4:
I: k = В
S:Распределите в порядке уменьшения предпочтительности товара для потребителя при следующих условиях. Товар А: предельная полезность 100, цена 10. Товар B: предельная полезность 150, цена 10. Товар C: предельная полезность 200 цена 15. Товар D: предельная полезность 300, цена 50:
I: k = A
S:Кто вывел формулу потребительского равновесия:
I: k = A
S:Представителями подхода, считающими, что полезность можно измерить являются:
I: k = A
S:Представителей подхода, считающих, что потребитель не точно определяет полезность какого-то блага, а осуществляет их ранжирование от более предпочтительных к менее предпочтительным называют:
I: k = A
S:Допустим, потребитель делает выбор между двумя товарами. Предельную полезность мобильного телефона он оценивает в 10 000 ютилей, а ноутбука в – 20 000 ютилей. Стоимость мобильного телефона составляет 5 000 ден. ед., а стоимость ноутбука – 30 000 ден. ед. Определите какой из этих товаров выберет потребитель:
-: все равно, так как полезности товаров одинаковые
-: нет правильного варианта
I: k =B
S:Установите соответствия:
L2: Карта безразличия
L4: Кривая безразличия
R1: Различные комбинации двух товаров, которые могут быть куплены при фиксированной величине дохода
R2: Совокупность кривых безразличия
R3: Способность товара удовлетворять какие-либо потребности
R4:Кривая, показывающая различные комбинации двух товаров, приносящих одинаковые полезности потребителю
I: k = B
S:Установите соответствия:
L1: Pa Qa + Pb Qb = I
L3:
R1: бюджетная линия
R2: предельную норму замещения товара Y товаром Х
R3: формула потребительского равновесия
I: k = A
S:Бюджетная линия может менять свое положение:
+: при изменении цены одного из товаров
-: при изменении технологии производства
-: при изменении государственных дотаций предприятиям
-: при изменении законодательства страны
I: k = В
S:Бюджетная линия на товар А по оси У сместится вверх, если:
-: цена товара А увеличилась
-: уменьшились доходы индивида
+: цена товара А снизилась
+: увеличились доходы индивида
I: k = В
S:Бюджетная линия на товар А по оси У сместится вниз, если:
+: цена товара А увеличилась
+: уменьшились доходы индивида
-: цена товара А снизилась
-: увеличились доходы индивида
I: k = В
S:Бюджетная линия может сместиться вправо, если:
-: доход потребителя уменьшился
-: цены на оба товара увеличились
+: доход потребителя увеличился
+: цены на оба товара снизились
I: k = B
S:Бюджетная линия может сместиться влево, если:
+: доход потребителя уменьшился
+: цены на оба товара увеличились
-: доход потребителя увеличился
-: цены на оба товара снизились
I: k = C
S:Величина предельной полезности составляет 110, изменение количества равна 2. Определите изменение общей полезности:
I: k = B
S:Установите соответствия:
L1: эффект дохода
L2: эффект замещения
L4: кривая безразличия
R1: изменение величины спроса на товар, вызванное ростом реального дохода от снижения цен
R2: изменение величины спроса, вызванное увеличением закупок подешевевшего товара, замещающего остальные товары с неизменными ценами, поскольку они стали теперь относительно более дорогими
R3: способность товара удовлетворять какие-либо потребности
R4:кривая, показывающая различные комбинации двух товаров, приносящих одинаковые полезности потребителю
I: k = B
S:Установите соответствия:
L1: эффект дохода
L2: эффект замещения
L3: бюджетная линия
L4: карта безразличия
R1: изменение величины спроса на товар, вызванное ростом реального дохода от снижения цен
R2: изменение величины спроса, вызванное увеличением закупок подешевевшего товара, замещающего остальные товары с неизменными ценами, поскольку они стали теперь относительно более дорогими
R3: различные комбинации двух товаров, которые могут быть куплены при фиксированной величине дохода
R4: совокупность кривых безразличия дохода
I: k = B
S:Установите соответствия:
L1: точкой потребительного оптимума
L2: предельной нормой замещения
L3: карта безразличия
R1: точка касания кривой безразличия и бюджетной линии называется
R2:количество товара А, от которого отказывается потребитель, чтобы приобрести большее количество товара В, называется
R3: совокупность кривых безразличия
R4: способность товара удовлетворять какие-либо потребности
I: k = A
S:Потребитель делает выбор между покупкой телевизора или холодильника. Предельную полезность телевизора он оценивает в 5 000 ютилей, а холодильника в – 8 000 ютилей. Стоимость телевизора составляет 15 000 ден. ед., а стоимость холодильника – 10 000 ден. ед. Определите, что выберет потребитель:
-: все равно, что покупать
-: нет правильного варианта
I: k = C
S:Величина предельной полезности составляет 10, изменение количества равно 5. Определите изменение общей полезности:
I: k = A
S:Набор товаров А и В, соответствующий каждой точке кривой безразличия, приносит потребителю:
-: одинаковую предельную полезность
-: различную предельную полезность
-: различную совокупную полезность
+: одинаковую совокупную полезность
I: k = A
S:Каждой точке бюджетной линии соответствует набор товаров А и В, который:
-: может быть потреблен в течение одного часа
-: может быть приобретен потребителем при данных затратах на производство
-: может быть реализован при данных ценах на товары
+: может быть приобретен потребителем при данном доходе и данных ценах на товары
I: k = A
S:Товары А и В являются взаимозаменяемыми, если:
Источник