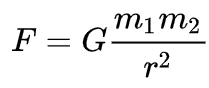Закон всемирного тяготения Ньютона
На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.
Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы — существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.
Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.
Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:
где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10 –11 .
Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.
Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.
Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли M и радиус Земли D , помня при этом, что, согласно второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.
Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.
Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.
Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.
Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.
Я допускаю, что кого-то из историков от моей версии хватит удар, но на самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.
Источник
О. о законе всемирного тяготения кратко
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ.
Закон всемирного тяготения был открыт Ньютоном в 1666 г. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
Здесь G — гравитационная постоянная, равная м;/(кг с;).
Легенда гласит, что Ньютон открыл закон всемирного тяготения после того, как яму упало на голову яблоко. Но скорее всего, всё с античных философов вроде Эпикура, которые объясняли тяготение взаимным любовным влечением физических тел. Но Ньютону дать научное, математически оформленное объяснение тяготению. Ньютон очень гордился открытием своего закона, но всё же скромно признавался, что смог сделать его, лишь «став на плечи гигантов».
Всё началось с Коперника, который открыл, что «она вертится», и задача раскрытия механизма солнечной системы обрела основу. Вслед за польским учёным Коперником, английский Гильберт (1540—1603) внес свою лепту в объяснение тяготения, предположив, силы тяготения подобны силе магнитов. Француз же Рене Декарт предположил, что тяготение создают вихри тонкой невидимой материи, а планеты подобны телам попавшим в водяные воронки. Но строгий порядок в мысли о тяготении внес Иоганна Кеплер (1571—1630), который вывел количественные законы движения планет. Потом Галилей добавил закон инерции и принцип независимости действия сил. А вот уже Роберт Гук (1635—1703) сделал практически первый эскиз закона: «Все небесные тела производят притяжение к их центрам, притягивая не только свои части, как мы это наблюдали на Земле, но и другие небесные тела, находящиеся в сфере их действия».
В 1684 г. астроном Эдмунд Галлей (1656 — 1742), догадавшись, что сила тяготения убывает обратно пропорционально квадрату расстояния, обратился к своему приятелю Ньютону с просьбой обсчитать эту идею, но оказалась, что тот уже давно всё подсчитал, но Королевское общество его расчёты не заценило. Галлей убедил Ньютона снова сдать свои результаты в Королевское общество, и тот отнес туда свой трактат «Предположения о движении». Таким образом миру стало известно о всемирном тяготении.
Через 200 лет после открытия Ньютоном своего закона в 1915 Альберт Эйнштейн создал общую теорию относительности. Оказалось, что теория Ньютона — приближение более общей теории, применимое при выполнении двух условий:
1. Гравитационный потенциал в исследуемой системе не слишком велик: .
2. Скорости движения в этой системе незначительны по сравнению со скоростью света: .
В рамках общей теории относительности, как и в других метрических теориях, постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, находящихся в пространстве-времени, а деформацией самого; пространства-времени, которая связана, в частности, с присутствием массы-энергии.
—
Но в сети можно найти массу роликов и текстов, показывающих что никакой гравитации нет. С вполне интересной аргументацией. Что же есть тогда? Вращение, заряд-электричество. То есть, самои основы классической и даже не очень классической физики имеют червоточенку. Во как.
.
Но в целом всё ещё интересней. Гегель например, критиковал Ньютона, за этот закон. Гравитация-притяжение в принципе не возможны. Возможно только давление-отталкивание. Ф. Энгельс эту мысль поддержал. Российский физик Федулаев пытается построить на этой основе физическую теорию. По-моему, у него получилось бы успешнее, если бы он принял гипотезу вывернутой (вогнутой) Земли.
Российский физик Вадим Ловчиков приводит немало аргументов, свидетельствующих, что Ньютон вообще не создавал теории всемирного тяготения. Вернадский считал также, что Ньютон критиковал теорию тяготения и не является её автором.
Источник
Закон всемирного тяготения Исаака Ньютона и гравитация
Как был открыт закон всемирного тяготения и почему Луна не падает на Землю.
Во вселенной существует всего одна сила, действие которой по-истине глобально и распространяется на все предметы – от мелких песчинок, до гигантских звезд. Это сила тяготения, сила гравитации.
Все знают историю про Исаака Ньютона и яблоко. Однако не все знают, что он пошел дальше и разобрался с Луной!
Закон всемирного тяготения был впервые сформулирован Исааком Ньютоном в 1666 году. Началось все с простого вопроса – почему Луна не падает на Землю (или не улетает от неё), в то время как яблоко, как высоко его не подбрасывай, в воздухе не зависнет. При этом, вполне очевидно, что Луна – штука гораздо более тяжелая, чем яблоко.
Ньютон провел довольно остроумный опыт. Нам известно, что на поверхности Земли, ускорение свободно падающего тела равно 9,81 м/с 2
При этом, учитывая, что наша планета имеет форму шара, ускорение 9,81 м/с 2 получается за 1 земной радиус (расстояние от центра планеты до поверхности).
Если же рассчитать, зная расстояние до Луны и период её обращения вокруг Земли, её ускорение, то мы получим значение меньше “яблочного” в 60 2 раз. Но ведь и Луна, находится от центра Земли в 60 раз дальше…
Наглядная иллюстрация разности ускорения.
“Совпадение” с цифрами показались Ньютону не случайными. Он предположил, что сила притяжения тела (в данном случае нашей планеты) не остается постоянной на удалении от него, а меняется обратно пропорционально квадрату расстояния до центра Земли. Короче говоря: чем больше расстояние – тем меньше сила притяжения.
Это предположение означало, что силу, которая удерживает Луну на ее орбите, можно рассматривать как силу притяжения Земли, ослабленную пропорционально отношению квадратов расстояний от центра Земли до Луны и от центра Земли до поверхности Земли.
Это, в свою очередь, позволило сформулировать и сам закон тяготения Ньютона: любые две частицы материи взаимно притягивают друг друга с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Математически закон записывается так:
Коэффициент G называется постоянной тяготения или гравитационной постоянной, её значение вычислено достаточно точно и составляет: 6,67⋅10 −11 м³/(кг·с²).
Тут может возникнуть вполне резонный вопрос: если гравитация есть у любого предмета, почему, к примеру, не притягиваются друг к другу камни, гайки, люди…. да даже металлические шарики, положи их рядом – не катятся друг к другу на встречу?
Ответ, конечно прост: вы посмотрите на значение гравитационной постоянной и вам станет очевидно, что сама по себе её величина ну очень мала. Настолько мала, что даже для таких крупных предметов как здания или горы её практически невозможно обнаружить и измерить – куда там людям или шарикам.
Другое дело – небесные тела вроде планет, звезд, галактик и т.п. Они обладают гигантскими массами, по порядку величины многократно превышающими численное значение G. Поэтому оказывается, что, несмотря на свою слабость, именно сила тяготения является главной, ведущей, управляющей движениями всех небесных тел. Именно закон тяготения описывает траектории движений планет и их спутников, а также звезд и даже звездных скоплений.
Наглядная схема разности гравитационных сил Земли и Луны. Наша планета изрядно «проминает» ткань пространства и не дает Луне убежать. Однако, чтобы совсем притянуть её к себе, сил не хватает. И слава богу!
Поскольку оказалось, что закон работает на огромных расстояниях от Земли, а значит, работал и миллиарды лет тому назад, закон тяготения принято называть законом всемирного тяготения, подчеркивая его всеобщность и фундаментальность в нашей Вселенной.
Считаю важным добавить: некоторые космологические модели предусматривают возможность медленного изменения гравитационной постоянной со временем, но на сегодняшний день экспериментально такое изменение достоверно не обнаружено, что позволяет считать G константой.
Открытие Исаака Ньютона позволило не только объяснить множественные “странности” в поведении массивных небесных тел: особенности в движении Луны, явление прецессии, приливы, сжатие газовых гигантов у полюсов, движения в системах двойных звезд, но также помогло «взвесить» Землю и другие планеты и даже предсказывать будущие открытия. Так, например, ещё в 1798 г. Пьер Лаплас фактически обосновал то явление, что мы сейчас называем “черной дырой”, рассчитав, что если некая звезда достигнет невероятной массы и плотности вещества, то её излучение не сможет уйти от неё и этот объект просто “исчезнет” для стороннего наблюдателя.
Источник