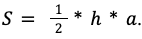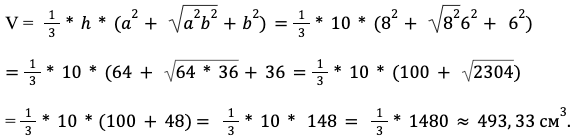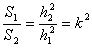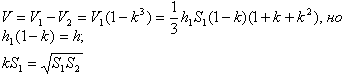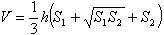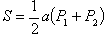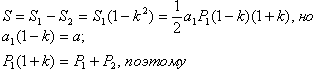Объем усеченной пирамиды как вывести

Что являет собою формула объема усеченной пирамиды четырехугольной?

Содержание:

Пирамидой называется объемное тело с многоугольником в основании – трёх-, четырёхугольник и т.д. Боковые грани – треугольники, выходящие из одной точки – его вершины. Геометрические тела бывают трехгранными (тетраэдр), правильными, произвольными, усеченными.

Понятие

Основание геометрического тела представлено правильным многоугольником, с расположенной над его центром вершиной. Свойства пирамиды:

• имеет равные боковые ребра с одинаковыми углами между ними и нижней поверхностью;
• боковые ребра – конгруэнтные равнобедренные трапеции;
• площадь боковых поверхностей является произведением боковой грани на половину суммы периметров обоих оснований.

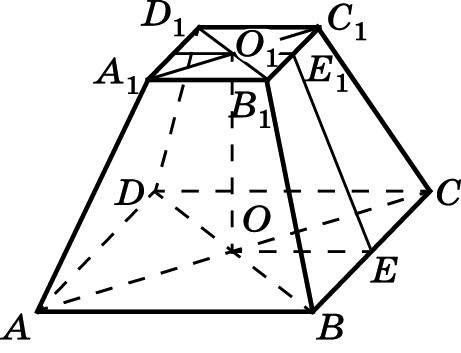
Усеченная пирамида – часть геометрического тела, ограниченная нижней гранью и параллельной ей плоскостью сечения. Верхняя, отсеченная, часть образует подобную пирамиду – уменьшенную в n раз. Если основание усеченного геометрического тела – неправильный многоугольник, она называется неправильной. Обладает разными боковыми гранями – это трапеции.

Правильная усеченная пирамида получается из правильного геометрического тела. Имеет равные боковые ребра и апофемы. Свойства:

• в сечении образуется подобный основанию многоугольник, он становится верхней гранью;
• площади оснований относятся как квадраты их отдаленности от изначальной вершины тела (до усечения).

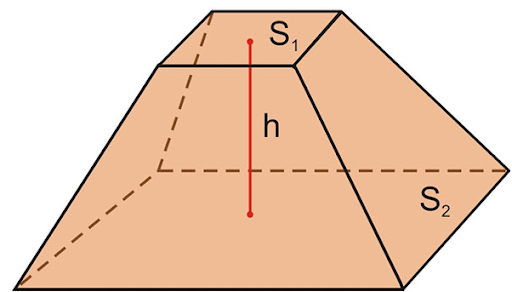
Объем усеченной пирамиды

Формула объема усеченной пирамиды:

• h – высота;
• S₁ и S₂ – площадь параллельных поверхностей.

В зависимости от формы нижней поверхности, формула объема усеченной пирамиды (четырехугольной или треугольной) остается неизменной. Меняются только способы вычисления площадей верхнего и нижнего многоугольников:

• Треугольник – площадь определяется как половина произведения длины треугольника на опущенную на него высоту.

Также можно воспользоваться формулой Герона или иной в зависимости от исходных данных.

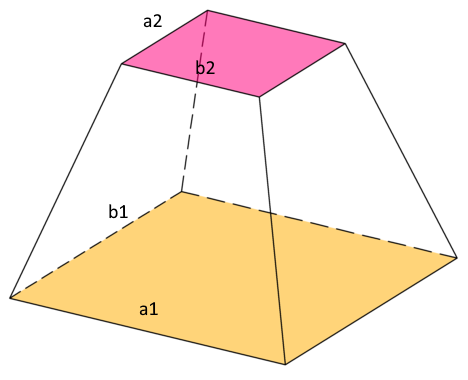
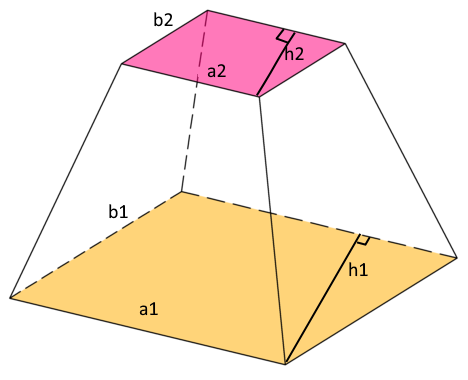
Рассмотрим, как найти объем усеченной пирамиды с квадратом в основании на примере. Известно, что:

• h = 10 см;
• a = 8, b = 6 см – стороны нижней и верхней граней.

, здесь:

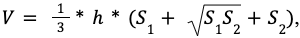
S₁ = a * a = a₂, S₂ = b* b = b₂ – стороны квадрата одинаковы.

Сложность задачи вычисления площади усеченной пирамиды может заключаться в определении площадей ее оснований, особенно если они имеют нестандартную форму (пятиугольник). Иногда в задаче предоставляются косвенные данные, например, диагонали прямоугольника, на основе которых придется отыскать площадь либо длину его сторон.

Источник

Материал по математике по теме «Усеченная пирамида»

Описание разработки

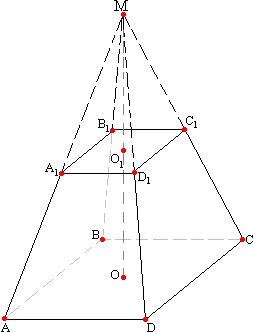
Определение. Часть пирамиды, образованная при сечении пирамиды плоскостью, параллельной её основанию, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.

На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h2/h1, или боковых ребер, или других соответствующих линейных размеров обеих пирамид. Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т. е. пощади оснований усеченной пирамиды) относятся, как

Здесь S1 — площадь нижнего основания, а S2 — площадь верхнего основания усеченной пирамиды. В таком же отношении находятся и боковые поверхности пирамид. Сходное правило имеется и для объемов.

Объемы подобных тел относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований.

Пусть дана усеченная пирамида с высотой h и площадями оснований S1 и S2. Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S2/S1. Высота усеченной пирамиды выражается как h = h1 — h2 = h1(1 — k). Теперь имеем для объема усеченной пирамиды (через V1 и V2 обозначены объемы полной и малой пирамид)

Полную информацию смотрите в файле.

Содержимое разработки

Определение . Часть пирамиды, образованная при сечении пирамиды плоскостью, параллельной её основанию, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.
На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h₂/h₁, или боковых ребер, или других соответствующих линейных размеров обеих пирамид. Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как

Здесь S₁ — площадь нижнего основания, а S₂ — площадь верхнего основания усеченной пирамиды. В таком же отношении находятся и боковые поверхности пирамид. Сходное правило имеется и для объемов.
Объемы подобных тел относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований.
Пусть дана усеченная пирамида с высотой h и площадями оснований S₁ и S₂. Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S₂/S₁. Высота усеченной пирамиды выражается как h = h₁ — h₂ = h₁(1 — k). Теперь имеем для объема усеченной пирамиды (через V₁ и V₂ обозначены объемы полной и малой пирамид)

k 2 S₁=S₂, поэтому

Теорема. Объем усеченной пирамиды можно вычислить по формуле:

При нахождении площади боковой поверхности усеченной пирамиды принципы нахождения ПБП обычной пирамиды не теряют актуальности:
Теорема . Если все апофемы усеченной пирамиды равны, то площадь её боковой поверхности можно вычислить по формуле:

Из этой теоремы можно получить подобные:
Теорема. Если все боковые грани усеченной пирамиды наклонены к плоскости основания под одинаковым углом, то площадь её боковой поверхности можно вычислить по формуле:

Теорема. Если пирамида правильная, то площадь её боковой поверхности можно вычислить по формуле:

При нахождении площади поверхности усеченной пирамиды, необладающей ни одним из перечисленных признаков, осуществляется вычисление площадей отдельных граней, а затем производится их суммирование.
Выведем эту формулу. Пусть S — площадь боковой поверхности усеченной пирамиды, обладающей одним из вышеперечисленных признаков, Р₁ и Р₂ — периметры оснований и а — длина апофемы. Рассуждаем точно так же, как и при выводе формулы для объема. Дополняем пирамиду верхней частью, имеем P₂ = kP₁, S₂=k 2 S₁, где k — коэффициент подобия, P₁ и P₂ — периметры оснований, а S₁ и S₂ — лощади боковых поверхностей всей полученной пирамиды и её верхней части соответственно. Для боковой поверхности найдем
(а₁ и а₂ — апофемы пирамид, а = а₁ — а₂ = а₁(1-k)):

Правильная усеченная пирамида также как и обычная правильная пирамида имеет особенности:
Теорема. В правильной усеченной n-угольной пирамиде все боковые ребра равны между собой.
Теорема. Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях рабнобедренной трапеции равны), поэтому:
Теорема. В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны.

Источник