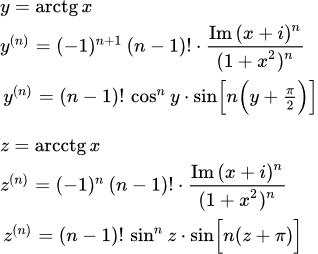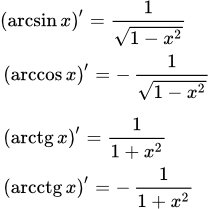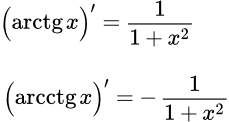Производная арктангенса как вывести

Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)

Вывод производных высших порядков арктангенса

Найдем производные высших порядков. Для этого разложим дробь на простейшие:

.
Здесь – мнимая единица, .

Тогда производную арктангенса первого порядка можно записать в следующем виде:
.

Дифференцируем раз и приводим дроби к общему знаменателю:

.
В числителе стоит разность комплексно сопряженных величин. Поэтому числитель является чисто мнимым. Пусть обозначает мнимую часть стоящего следом выражения. Тогда производную арктангенса n-го порядка можно записать в следующем виде:
(2) .
Здесь выражение в числителе является многочленом степени .

Производные арктангенса со второго по пятый порядок

Вычислим производные арктангенса нескольких высших порядков, используя формулу (2). Для этого мы используем формулу бинома Ньютона:
.
Также используем свойства мнимой единицы:
;
;
.
И так далее.

Производная второго порядка.
При имеем:
;
;
.

Производная третьего порядка.
При имеем:
;
;
.

Производная четвертого порядка.
При получаем:
;
;
.

Наконец, вычислим производную пятого порядка.
Подставим :

;
;
.

Другой вид производных арктангенса высших порядков

Оказывается, что формулу производной арктангенса n-го порядка можно представить в удобном виде, если выразить производную не через независимую переменную x , а через сам арктангенс.

Итак, пусть
.
Используем формулу (2) производной n-го порядка:
(2) .
Подставим :
;
;

;
.
Применим формулу Эйлера. Тогда
;
;
;

.

Тем самым мы получили производную арктангенса n-го порядка, выраженную через сам арктангенс:
(3) .
Здесь .

Производные высших порядков арккотангенса

Чтобы получить производные высших порядков арккотангенса, воспользуемся связью между арктангенсом и арккотангенсом:
(4) .
Дифференцируя это уравнение n раз и учитывая, что производная постоянной равна нулю, получим производную арккотангенса n-го порядка:
(5) .

Другой вид производных арккотангенса высших порядков

Пусть
.
Выразим производную n-го порядка арккотангенса через z . Для этого можно подставить в (5) . Но мы используем формулу (3) для n-ой производной арктангенса и формулу (4), связывающую арккотангенс с арктангенсом. Пусть
.
Тогда . Подставим в (3):
(3) ;
.
Далее замечаем, что
;
.
Тогда
(6) .
Это и есть искомая формула производной n-го порядка арккотангенса.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 17-05-2017

Источник

Вывод производных обратных тригонометрических функций

Вывод производных арксинуса и арккосинуса

Сначала выведем формулу производной арксинуса. Пусть
y = arcsin x .
Поскольку арксинус есть функция, обратная к синусу, то
.
Здесь y – функция от x . Дифференцируем по переменной x :
.
Применяем формулу производной сложной функции:
.
Итак, мы нашли:
.

Поскольку , то . Тогда
.
И предыдущая формула принимает вид:
. Отсюда
.

Точно таким способом можно получить формулу производной арккосинуса. Однако проще воспользоваться формулой, связывающей обратные тригонометрические функции:
.
Тогда
.

Более подробно изложение представлено на странице “Вывод производных арксинуса и арккосинуса”. Там дается вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.

Вывод производных арктангенса и арккотангенса

Таким же способом найдем производные арктангенса и арккотангенса.

Пусть
y = arctg x .
Арктангенс есть функция, обратная к тангенсу:
.
Дифференцируем по переменной x :
.
Применяем формулу производной сложной функции:
.
Итак, мы нашли:
.

Далее выразим через и учтем, что .
.
Тогда
.
Отсюда
.

См. “Вывод производных арктангенса и арккотангенса”. На этой странице изложен вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.

Производные высших порядков

Далее мы приводим некоторые соотношения и выражения для производных высших порядков от обратных тригонометрических функций. Полное изложение вывода формул производных высших порядков представлено на страницах Вывод производных высших порядков арксинуса и арккосинуса и Вывод производных высших порядков арктангенса и арккотангенса.

Производные арксинуса

Пусть
.
Производную первого порядка от арксинуса мы уже нашли:
.
Дифференцируя, находим производную второго порядка:
;
.
Ее также можно записать в следующем виде:
.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
.

Дифференцируя это уравнение, можно найти производные высших порядков.

Производная арксинуса n-го порядка

Производная арксинуса n-го порядка имеет следующий вид:
,
где – многочлен степени . Он определяется по формулам:
;
.
Здесь .

Многочлен удовлетворяет дифференциальному уравнению:
.

Производная арккосинуса n-го порядка

Производные для арккосинуса получаются из производных для арксинуса с помощью тригонометрической формулы:
.
Поэтому производные этих функций отличаются только знаком:
.

Производные арктангенса

Пусть . Мы нашли производную арккотангенса первого порядка:
.

Разложим дробь на простейшие:

.
Здесь – мнимая единица, .

Дифференцируем раз и приводим дробь к общему знаменателю:

.

Производная арктангенса n-го порядка

Таким образом, производную арктангенса n-го порядка можно представить несколькими способами:
;
.

Производные арккотангенса

Пусть теперь . Применим формулу, связывающей обратные тригонометрические функции:
.
Тогда производная n-го порядка от арккотангенса отличаются только знаком от производной арктангенса:
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 20-04-2017

Источник

Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′

Вывод производной арктангенса

Здесь мы полагаем, что нам известна производная тангенса:
.
Далее мы выводим формулу производной арктангенса, учитывая, что арктангенс является функцией, обратной к тангенсу.

По формуле производной обратной функции

Рассмотрим функцию арктангенс:
y = arctg x .
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от – π/2 до + π/2 :
.
Арктангенс является функцией, обратной к тангенсу:
x = tg y .

Для определения его производной, применим формулу производной обратной функции:
(1) .

Производная тангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y . Тогда
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arctg x ;
x = tg y .

Теперь выразим правую часть формулы (2) через переменную x . Для этого воспользуемся формулой и выполним преобразования:
.
Отсюда
.
Подставим в (2):
.

Тем самым мы вывели формулу производной арктангенса:
.

Второй способ

Поскольку арктангенс и тангенс являются взаимно обратными функциями, то
(3) .
Продифференцируем это уравнение по переменной x . То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .

Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.

Вывод производной арккотангенса

Используя связь между арктангенсом и арккотангенсом

Производную арккотангенса можно получить из производной арктангенса, если воспользоваться связью между арктангенсом и арккотангенсом:
.
Отсюда
.

По формуле производной обратной функции

Рассмотрим функцию арккотангенс:
y = arcctg x .
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от 0 до π :
.
Арккотангенс является функцией, обратной к котангенсу:
x = ctg y .

Для определения его производной, применим формулу производной обратной функции:
(1) .

Считаем, что производная котангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y . Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arcctg x ;
x = ctg y .

Выразим правую часть формулы (5) через переменную x . Для этого выполним преобразования:
.
Отсюда
.
Подставим в (5):
.

Таким образом, мы вывели формулу производной арккотангенса:
.

Второй способ

Поскольку арккотангенс и котангенс являются взаимно обратными функциями, то
(6) .
Продифференцируем это уравнение по переменной x :
(7) .

Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.

Автор: Олег Одинцов . Опубликовано: 07-05-2017

Источник

Производная арктангенса как вывести

К основным тригонометрическим функциям относятся следующие \(6\) функций: синус (\(\sin x\)) , косинус (\(\cos x\)) , тангенс (\(\textx\) или \(\tan x\)) , котангенс (\(\textx\) или \(\cot x\)) , секанс (\(\sec x\)) и косеканс (\(\csc x\)) .

Для каждой из этих функций существует обратная тригонометрическая функция . Они называются, соответственно, арксинус (\(\arcsin x\)) , арккосинус (\(\arccos x\)) , арктангенс (\(\textx\) или \(\arctan x\)) , арккотангенс (\(\textx\) или \(\textx\)) , арксеканс (\(\textx\)) и арккосеканс (\(\textx\)) .

Все указанные функции непрерывны и дифференцируемы в своей области определения. Далее мы составим список производных для этих \(12\) функций.

Производные обратных тригонометрических функций можно вывести, используя теорему о производной обратной функции . Так, например, для функции \(y = f\left( x \right) = \arcsin x\) обратной функцией является синус, т.е. \(x = \varphi \left( y \right) = \sin y.\) Тогда производная арксинуса равна: \[ <<\left( <\arcsin x>\right)^\prime > = f’\left( x \right) = \frac<1><<\varphi '\left( y \right)>> > = <\frac<1> <<<<\left( <\sin y>\right)>^\prime >>> > = <\frac<1><<\cos y>> > = <\frac<1><<\sqrt <1 - <\sin^2>y> >> > = <\frac<1><<\sqrt <1 - <\sin^2>\left( <\arcsin x>\right)> >> > = <\frac<1><<\sqrt <1 - > >>\;\;\left( < - 1 арксеканса всегда положительна.

Производная

Область определения

\( <\left( <\sin x>\right)^\prime > = \cos x\)

\(- \infty линейные свойства производной , правило дифференцирования сложной функции и формулу двойного угла , получаем: \[ \right)^\prime > > = <<\left( <\cos 2x>\right)^\prime > — <\left( <2\sin x>\right)^\prime > > = <\left( < - \sin 2x>\right) \cdot <\left( <2x>\right)^\prime > — 2 <\left( <\sin x>\right)^\prime > > = < - 2\sin 2x - 2\cos x >= < - 2\sin x\cos x - 2\cos x >= < - 2\cos x\left( <\sin x + 1>\right).> \]

Заметим, что функция арксинус определена на отрезке \(\left[ < - 1,1>\right]\). В нашем случае условие, определяющее допустимые значения \(x\), выглядит так: \[ <- 1 \le \frac<<1 - >><<1 + >> \le 1,>\;\; <\Rightarrow - 1 - \le 1 — \le 1 + ,>\;\; <\Rightarrow \left\< <\begin<*<20>> < - 1 - \le 1 — >\\ <1 - \le 1 + > \end> \right.,>\;\; <\Rightarrow \left\< <\begin<*<20>> < - 1 \le 1>\\ < - \le > \end> \right..> \] Видно, что данные неравенства соблюдаются для любых действительных \(x\).

Источник

Производная обратной функции

В этой статье мы расскажем, что из себя представляет производная обратной функции и как ее вычислить. Перед изучением данной темы советуем повторить, что такое обратная функция и какими свойствами она обладает.

Чтобы избежать разночтений, мы будем обозначать аргумент функции, по которому она дифференцируется, в нижнем регистре, т.е. запись f x ‘ ( x ) будет означать производную функции f ( x ) по x .

Для начала определим правило, по которому производится вычисление производной обратной функции.

Допустим, у нас есть две взаимно обратные функции x = g ( y ) и y = f ( x ) , которые определены на соответствующих интервалах y ∈ c ; d и x ∈ [ a ; b ] . Если у нас есть некая точка x 0 ∈ [ a ; b ] , в которой расположена конечная производная f ( x ) , отличная от 0 , то должна быть и конечная производная g ( y ) , такая, что g y ‘ ( y 0 ) = 1 f x ‘ ( x 0 ) . Иначе это можно записать как f x ‘ ( x 0 ) = 1 g y ‘ ( y 0 ) .

Данное правило может быть сформулировано для любого x , принадлежащего интервалу [ a ; b ] . Тогда мы получим следующее: g y ‘ ( y 0 ) = 1 f x ‘ ( x 0 ) , f x ‘ ( x 0 ) = 1 g y ‘ ( y 0 ) . Истинность этих формул можно проверить с помощью следующих рассуждений.

У нас есть натуральный логарифм вида y = f ( x ) = ln x , где y является функцией, а x – аргументом. Найдем его обратную функцию. Для этого нам потребуется разрешить уравнение относительно x . Получим x = g ( y ) = e y (здесь x будет функцией, а y – ее аргументом). Значит, функции x = g ( y ) = e y и y = f ( x ) = ln x по отношению друг к другу являются взаимно обратными.

Проверим значения в таблице производных: y x ‘ = f x ‘ ( x ) = ln x x ‘ = 1 x , а x y ‘ = g y ‘ ( y ) = e y y ‘ = e y .

Тот же результат мы получим при использовании формулы обратных производных:

g y ‘ ( y ) = 1 f x ‘ ( x ) = 1 ( ln x ) x ‘ = 1 1 x = x = e y f x ‘ ( x ) = 1 g y ‘ ( y ) = 1 e y y ‘ = 1 e y = 1 e l n x = 1 x

Поскольку полученный результат соответствует значению, указанному в таблице производных, то данная формула будет верна.

Используя эти знания, мы можем перейти к доказательству формул производных обратных тригонометрических функций.

Производные функции арксинус и арккосинус

Первое, что мы сделаем, – научимся определять производную функции арксинус.

Поскольку y = a r c sin x , x ∈ — 1 ; 1 , то обратная функция будет выглядеть как x = sin y , y ∈ — π 2 ; π 2 .

Берем нужную формулу и вычисляем:

y x ‘ = ( arcsin x ) x ‘ = 1 ( sin y ) y ‘ = 1 cos y = 1 cos ( arcsin x )

Теперь нам надо преобразовать полученное выражение.

Поскольку область значения арксинуса представляет собой промежуток arcsin x ∈ — π 2 ; π 2 , значит, cos ( arcsin x ) ≥ 0 (при необходимости повторите материал об основных элементарных функциях, их свойствах и графиках).

Следовательно, cos ( arcsin x ) = 1 — sin 2 ( arcsin x ) — 1 — x 2 . Выражение cos ( arcsin x ) = 1 — sin 2 ( arcsin x ) — 1 — x 2 мы рассматривать не будем.

Мы получили, что arcsin x x ‘ = 1 cos ( arcsin x ) = 1 1 — x 2 .

Производная арксинуса определена на промежутке ( — 1 ; 1 ) .

Для функции арккосинус все вычисления будут точно такими же.

y x ‘ = ( a r c cos ) x ‘ = 1 ( cos y ) y ‘ = 1 — sin y = — 1 sin ( a r c cos x ) = = — 1 1 — cos 2 ( a r c cos x ) = — 1 1 — x 2

Производные функции арктангенс и арккотангенс

Теперь вычислим производную арктангенса.

Поскольку для y = a r c t g x , x ∈ ( — ∞ ; + ∞ ) обратной функцией будет x = t g y , y ∈ — π 2 ; π 2 , то y ‘ x = a r c t g x x ‘ = 1 ( t g y ) y ‘ = 1 1 cos 2 y = cos 2 ( a r c t g x ) .

Для упрощения результата нужно выразить арктангенс через арккосинус.

Допустим, что a r c t g x = z , значит:

t g ( a r c t g x ) = t g z ⇒ x = t g z = sin z cos z = 1 — cos 2 z cos z ⇒ x · cos z = 1 — cos 2 z ⇒ x 2 · cos 2 z = 1 — cos 2 z ⇒ ( x 2 + 1 ) · cos 2 z = 1 ⇒ cos 2 z = 1 x 2 + 1 ⇒ cos z = 1 x 2 + 1 ⇒ z = a r c cos 1 x 2 + 1 ⇒ a r c t g x = a r c cos 1 x 2 + 1

Следовательно, можно записать так:

a r c t g x x ‘ = cos 2 ( a r c t g x ) = = cos 2 a r c cos 1 x 2 + 1 = 1 x 2 + 1 2 = 1 x 2 + 1

Для вычисления производной арккотангенса действуем по аналогии:

y x ‘ = ( a r c c t g x ) x ‘ = 1 ( c t g y ) y ‘ = 1 — 1 sin 2 y = — sin 2 ( a r c c t g x ) = = — sin 2 a r c sin 1 x 2 + 1 = — 1 x 2 + 1

Источник