Расстояние от точки до прямой как вывести

Расстояние от точки до прямой в пространстве.

Формула для вычисления расстояния от точки до прямой в пространстве

Если s = — направляющий вектор прямой l , M₁( x ₁, y ₁, z ₁) — точка лежащей на прямой, тогда расстояние от точки M₀( x ₀, y ₀, z ₀) до прямой l можно найти, используя формулу

Вывод формулы вычисления расстояния от точки до прямой в пространстве

Если задано уравнение прямой l то несложно найти s = — направляющий вектор прямой и M₁( x ₁, y ₁, z ₁) — координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

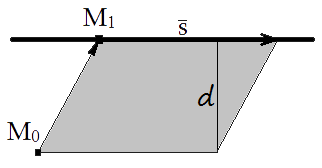
С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

В нашем случае высота будет равна расстоянию от точки до плоскости d , а сторона параллелограмма равна модулю направляющего вектора s .

Приравняв площади несложно получить формулу расстояния от точки до прямой.

Примеры задач на вычисление расстояния от точки до прямой в пространстве

x — 3	=	y — 1	=	z + 1
2		1		2

Из уравнения прямой получим:

s = < 2; 1; 2 >— направляющий вектор прямой;
M₁(3; 1; -1) — точка лежащая на прямой.

M0M1 × s =	i	j	k	=
	3	-1	-4
	2	1	2

d = | M₀M₁ × s | | s | = √ 2 2 + (-14) 2 + 5 2 √ 2 2 + 1 2 + 2 2 = √ 225 √ 9 = 15 3 = 5

Ответ: расстояние от точки до прямой равно 5.

Источник

Расстояние от точки до прямой онлайн

С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Расстояние от точки до прямой − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Расстояние от точки до прямой на плоскости

Пусть в двухмерном пространстве задана точка M₀(x₀, y₀) и прямая L:

,

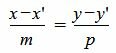(1)

где q=(m,p) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (1)(Рис.1).

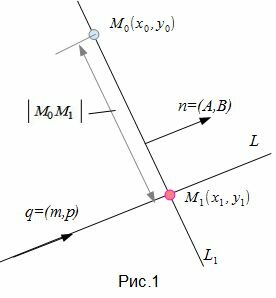Алгоритм нахождения расстояния от точки M₀ до прямой L содержит следующие шаги:

• построить прямую L₁, проходящую через точку M₀ и перпендикулярную прямой L,
• найти пересечение прямых L и L₁(точка M₁)
• найти найти расстояние между точками M₀ и M₁.

Уравнение прямой, проходящей через точку M₀(x₀, y₀) имеет следующий вид:

Как видно из рисунка Рис.1, для того, чтобы прямая L₁ была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L₁, поэтому в качестве нормального вектора прямой L₁ достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L₁, представленной уравнением (2) можно записать так:

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M₀ на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

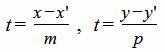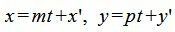(5)

Подставим значения x и y в (4):

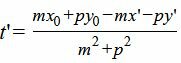(6)

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M₀ на прямую L:

Далее находим расстояние между точками M₀ и M₁ используя формулу:

.

(7)

Пример 1. Найти расстояние от точки M₀(−6, 2) до прямой

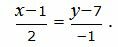(8)

Направляющий вектор прямой (8) имеет вид:

Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x₀, y₀, x’, y’ в (6):

,

Подставляя значение t в (5), получим:

Вычислим расстояние между точками M₀(-6, 2) и M₁

Упростим и решим:

Расстояние от точки M₀(-6, 2) до прямой (8) :

2. Расстояние от точки до прямой в пространстве

,

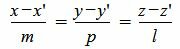(9)

где q=(m, p, l) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (9)(Рис.2).

Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:

• построить плоскость α, проходящую через точку M₀ и перпендикулярную прямой L,
• найти пересечение плоскости α и прямой L(точка M₁)
• найти расстояние между точками M₀ и M₁.

где n=(A,B,C) нормальный вектор плоскости α.

Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M₀ на прямую L, выведем параметрическое уравнение прямой (9):

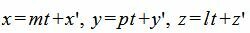(12)

Подставим значения x и y в (11):

m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0

(13)

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M₀ на прямую L:

Далее вычисляем расстояние между точками M₀ и M₁ используя формулу

,

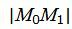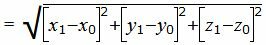(14)

которое является расстоянием между точкой M₀ и прямой (9).

Пример 2. Найти расстояние от точки M₀(1, 2, 1) до прямой

(15)

Направляющий вектор прямой (15) имеет вид:

Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x₀, y₀, z₀ x’, y’, z’ в (13):

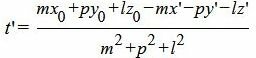Подставляя значение t=t’ в (12), получим координаты точки M₁:

,

,

.

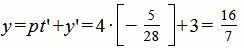Далее, используя формулу (14) вычисляем расстояние от точки M₀ до прямой (15):

.

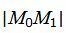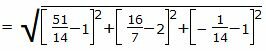Упростим и решим:

.

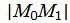Расстояние от точки M₀(1, 2, 1) до прямой (15) :

Источник

Расстояние от точки до прямой

Вы будете перенаправлены на Автор24

Основные определения и теоремы

Расстояние — это мера, характеризующая удалённость нескольких объектов друг относительно друга. Термин “расстояние” применим как в пространстве, так и на плоскости.

Рассмотрим небольшую иллюстрацию.

Мы видим на рисунке 2 точки. Необходимо найти расстояние между ними.

Для выполнения данной задачи необходимо использовать любой измерительный инструмент, например, линейку.

Необходимо приложить его начало к одной из точек, а конец к другой, и списать полученное с линейки число.

Также для измерения можно использовать, например, циркуль. С помощью него можно даже измерять толщину складок жира, прикладывая циркуль после снятия замера к линейке.

Очень часто для обозначения расстояния используют греческую букву $ρ$.

Перейдём к рассмотрению частного случая: поиску расстояния между точкой и прямой.

Расстояние между точкой и прямой

Рассматривая прямую и точку, не возлежащую на ней, следует помнить, что они всегда образуют плоскость по одной из основных аксиом объёмной геометрии, поэтому рассматривать эту задачу можно как одну из планиметрических.

Рисунок 3. Точка и не проходящая через неё прямая — служат характеристиками плоскости

Теорему, об образовании одной-единственной плоскости точкой и прямой можно вывести из аксиомы, в которой говорится, что три точки описывают плоскость.

Готовые работы на аналогичную тему

Дело в том, что на любой прямой всегда можно отметить 2 произвольные несовпадающие точки, а некая третья точка у нас уже дана. Вот и всё доказательство теоремы.

Расстояние между точкой и прямой — это перпендикуляр, который опускают с этой прямой в рассматриваемую точку.

Рассмотрим, что же такое расстояние от точки до прямой на примере задачи ниже.

Расстояние от точки до прямой на плоскости

Рисунок 4. Найти расстояние от точки до прямой

Найдите расстояние от $l$ до $X$.

Опустим из точки $X$ перпендикуляр на прямую $l$. Также на прямой отметим любую точку, не совпадающую с точкой пересечения перпендикуляра из точки $X$ с прямой $l$, назовём её $Z$.

У нас получился прямоугольный треугольник $XYZ$.

Гипотенуза в этом треугольнике, как мы знаем, лежит напротив прямого угла, причём гипотенуза является самой длинной стороной, значит, кратчайшим путём между точкой и прямой будет $YX$, являющийся перпендикуляром.

Причём длина $XY$ всегда будет меньше длины $XZ$ вне зависимости от того, где именно на прямой поставить точку $Z$.

Одной из наиболее частых задач по данной теме на плоскости и в пространстве является определение расстояния от прямой до точки по координатам точки и уравнению прямой.

На практике обычно не очень удобно заниматься таким построением в масштабе 1:1, поэтому обычно поиск кратчайшей длины между точкой и прямой осуществляется аналитически.

Рассмотрим решение такой задачи на плоскости.

Дано уравнение некой прямой $m$: $y= 3x + 2$ и точка $M$, не возлежащая на ней, её икс и игрек $(2;0)$.

Определить расстояние между точкой и прямой.

Опускаем перпендикуляр из точки $M$ на прямую $m$.

Теперь, для того чтобы высчитать его длину, нужно найти координаты пересечения перпендикуляра, опущенного из точки $M$ с прямой $m$. Назовём точку их пересечения $D$.

Для того чтобы найти точку пересечения перпендикуляра, опущенного из нашей точки на прямую $m$, необходимо сначала получить уравнение этого перпендикуляра.

Для этого перепишем уравнение прямой $m$ в общем виде: $3x-y+2=0$.

При записи в такой форме не трудно увидеть, что нормальный вектор этой прямой имеет координаты $(3;-1)$.

Нормальный вектор для этой прямой является направляющим для перпендикуляра.

Также нам известно, что этот перпендикуляр проходит через точку $M$ с координатами $(2;0)$.

Следовательно, мы можем записать его уравнение:

Для того чтобы найти координаты точки пересечения перпендикуляра $MD$ с прямой $m$, необходимо решить систему уравнений:

Для этого выражаем $y$ из второго уравнения:

И затем подставляем его в первое:

Избавляемся от знаменателя, умножив всё на $3$:

Подставляем полученный икс во второе уравнение:

То есть точка пересечения перпендикуляра с прямой $m$ имеет координаты $(-0,4;0,8)$.

Теперь найдём длину $MD$:

Ответ: расстояние между точкой и прямой равно $0,89$.

Расстояние от точки до прямой в пространстве

При определении расстояния от точки до прямой в пространстве можно воспользоваться следующей формулой:

$ρ = \frac<\sqrt<\begin <|cc|>y_1 – y_0 & z_1 — z_0\\ m_1 & n_1 \\ \end^2 + \begin <|cc|>x_1 – x_0 & z_1 — z_0\\ l_1 & n_1 \\ \end^2 + \begin <|cc|>x_1 – x_0 & y_1 – y_0\\ l_1 & m_1 \\ \end^2>><\sqrt>$

В этой формуле $x_0, y_0, z_0$ — координаты точки, $x_1, y_1, z_1$ — координаты нормального вектора заданной прямой, а $l_1, m_1, n_1$ — координаты направляющего вектора прямой.

Эта формула также выведена из построений, аналогичных построением при решении подобной задачи на плоскости, но выглядит она более тяжеловесно.

Однако, этого не стоит пугаться, так как довольно удобно пользоваться.

Но, возможно, что новичкам перед её использованием придётся ознакомиться с тем, как высчитывать определитель матрицы.

Рассмотрим задачу с использованием этой формулы.

Дана прямая $w$ $\frac<1>=\frac <2>=\frac<4>$ и точка $K$ c координатами $(1;2;3)$.

Найдите расстояние от $w$ до $K$ в пространстве.

Направляющий вектор для заданной прямой имеет координаты $<1;2;4>$, а нормальный вектор — $<5;-1;4>$.

Подставим все эти числа в формулу для нахождения расстояния:

Расстояние между прямой и точкой в данном случае составит $5,080$.

Источник