- Уравнение неразрывности
- Уравнение расхода для несжимаемой жидкости
- Физический смысл уравнения неразрывности
- Уравнение неразрывности и уравнение Бернулли.
- Уравнение неразрывности потока жидкости
- Уравнение неразрывности струи жидкости. Уравнение Бернулли.
- Видео по теме уравнение неразрывности
- 4.2 Уравнение неразрывности для несжимаемой жидкости
- 4.3 Вязкость (внутренние трение) жидкости
Уравнение неразрывности
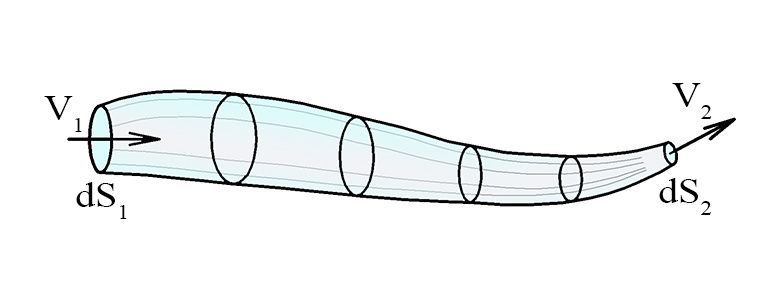
Рассмотрим элементарную струйку жидкости, имеющую бесконечно малые площади сечений.
В этих условиях можно считать истинную скорость v одинаковой во всех точках каждого сечения. Значит объемный расход для этой струйки можно определить, как:
где dS — площадь сечения струйки.
Для потока конечных размеров расход можно определить, как сумму элементарных расходов струек:
Если для расчтеов выбрать среднюю по сечению скорость, то расход можно вычислить по формуле:
Основываясь на законе сохранения вещества, для установившегося течения несжимаемой жидкости, можно вывод, что объемный расход во всех сечениях элементарной струйки будет постоянным:
Полученную зависимость называют уравнением расхода для элементарной струйки несжимаемой жидкости.
Уравнение расхода для несжимаемой жидкости
Для потока, ограниченного непроницаемыми стенками, уравнение расхода можно записать в следующем виде:
Полученную зависимость называют уравнением расхода потока несжимаемой жидкости или уравнением неразрывности.
Физический смысл уравнения неразрывности
Уравнение расходов является следствием закона сохранения вещества для условий неразрывного движения малосжимаемой жидкости, по этой причине его также называют уравнением неразрывности.
Из уравнения следует, что при заданном расходе, средние скорости в потоке зависят только от площадей нормальных сечений, эта зависимость является обратно пропорциональной.
Если на участке между расчетными сечениями нет притока и отбора жидкости, то объемный расход будет постоянным:
Уравнения Бернулли и неразрывности позволяют установить взаимосвязь между параметрами плавно изменяющегося потока жидкости в различных сечениях.
Источник
Уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.
Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.
Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.
Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.
Содержание статьи
Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.
Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υср .
Таким образом уравнение расхода для потока будет
υср – средняя скорость потока
F – площадь сечения потока.
Уравнение неразрывности потока жидкости
Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.
Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный
а через сечение 2-2 из него же вытекает объем, равный
Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.
Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.
Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что
т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.
При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.
Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.
Если всё это записать в виде формулы, то
где W – приращение кинетической энергии = m * υ 2 / 2
ΣA – сумма работ действующих сил = P *ΔS
В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.
Теперь рассмотрим обе части этого выражения по порядку.
Приращение кинетической энергии ΔW
В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.
Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.
Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен
масса в этом случае получается равной
Подставляя все это в выражение для кинетической энергии получаем цепочку
ΔW = m * υ 2 2 / 2 — m * υ 2 1 / 2 = ρ * q * ΔТ * υ 2 2 / 2 — ρ * q * ΔТ * υ 2 1 / 2
Работа сил действующих на систему ΣA
Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести AТ равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.
Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.
Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.
Силы давления АД , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.
Суммарно работа сил давления будет
Подставляя в начальное уравнение
Полученные выражения для ΔW и ΣA получаем
Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые
Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:
Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2
В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Видео по теме уравнение неразрывности
Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.
Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.
Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.
Источник
4.2 Уравнение неразрывности для несжимаемой жидкости
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рисунок 6).
Рисунок 6 Графическое изображение движения жидкости
Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2 (рис. 46). За время dt через сечение S проходит объем жидкости Sυdt; следовательно, за 1 с через S1 пройдет объем жидкости S1υ1, где υ1 -скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2υ2, где υ2 — скорость течения жидкости в месте сечения S2. Если жидкость несжимаема, то через сечение S2 пройдет такой же объем жидкости, как и через сечение S1 т. е.
Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (2) называется уравнением неразрывности для несжимаемой жидкости.
Рисунок 7 Иллюстрация уравнения неразрывности
4.3 Вязкость (внутренние трение) жидкости
Вязкостью или внутренним трением в качественном смысле называется свойство всех веществ оказывать сопротивление деформации сдвига, пропорциональное градиенту скорости. Вязкость (внутреннее трение) — это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.
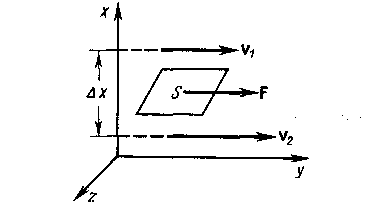
Рисунок 7 Иллюстрация, поясняющая формулу Ньютона
Коэффициент вязкости есть физическая величина, характеризующая силу внутреннего трения в жидкости. Сила трения 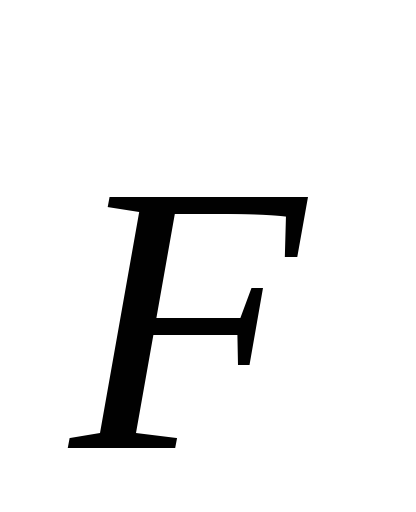

где 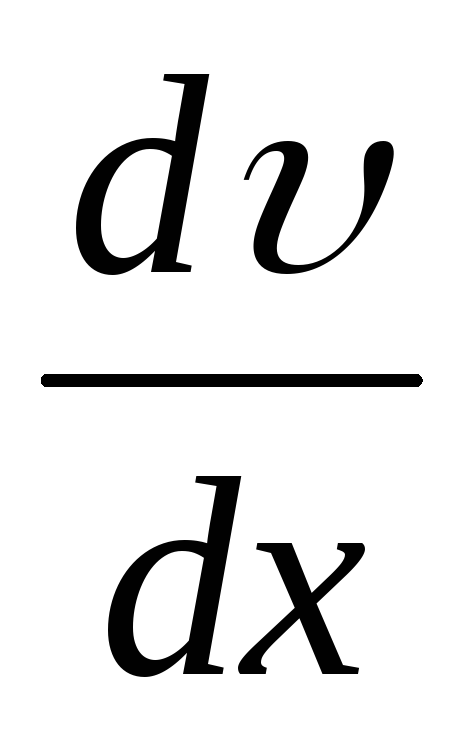


Единица вязкости — паскаль-секунда (Па • с): 1 Па • с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения в 1 Н на 1 м 2 поверхности касания слоев (1 Па • с = 1 Н • с/м 2 ).
Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают.
Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей η с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18 — 40 °С падает в четыре раза. Приборы, служащие для измерения вязкости, называются вискозиметрами. Вискозиметрия (лат. viscous – клейкий и греч. metre – мерю) – раздел физики, занимающийся методами измерения вязкости (внутреннего трения). Вязкость это свойство жидкостей или газов оказывать сопротивление перемещению или сдвигу одной их части относительно другой.
В некоторых случаях вместо определенной выше динамической вязкости удобнее пользоваться кинематической вязкостью — отношением динамической вязкости η к плотности ρ жидкости или газа:
Иногда вязкость растворов характеризуется относительной вязкостью —
отношением вязкости раствора к вязкости растворителя.
Возникновение сопротивления, обусловленного вязкостью жидкости, объясняется следующим образом.
Представим себе две пластинки, разделенные плоскопараллельным слоем жидкости (см. рисунок 8)
Рисунок 8 Иллюстрация объяснения возникающего сопротивления, обусловленного вязкостью жидкости
Рассмотрим, что произойдет, если начать перемещать верхнюю пластинку относительно нижней в направлении, указанном стрелкой. Мысленно разобьем жидкость на тончайшие слои. Молекулы жидкости, ближайшие к верхней пластинке, прилипают к ней, и в силу этого начинают перемещаться вместе с пластинкой с той же скоростью. Эти молекулы в свою очередь увлекают молекулы следующего слоя и т.д. Слои молекул, непосредственно прилегающих к нижней неподвижной пластине, остаются в покое, а остальные слои перемещаются, скользя друг по другу со скоростями тем большими, чем больше их расстояние от нижнего слоя. Вязкость жидкости проявляется в возникновении силы, препятствующей относительному сдвигу соприкасающихся слоев жидкости, а, следовательно, и сдвигу пластинок относительно друг друга.
Величина сопротивления, обусловленной вязкостью жидкости, зависит от разности скоростей между ее слоями и расстояния между ними.
Чем больше меняется скорость жидкости при переходе от слоя к слою, тем больше величина вязкого сопротивления.
Чтобы охарактеризовать величину изменения скорости, измерим разность скоростей (υ1 — υ2 = Δυ) двух слоев жидкости и расстояние Δу между этими слоями, отсчитываемое по нормали к направлению скорости. Предел отношения этих двух величин

называется градиентом скорости. Если конфигурация поверхностей такова, что скорость слоя пропорциональна нормальной координате
( υ = ky ), то dυ/dy = dυ/dy, (6)
т.е. градиент скорости равен падению скоростей на единицу длины. Этот случай имеет место между параллельными плоскостями
При ламинарном течении (т.е. без завихрений) сила внутреннего трения пропорциональна градиенту скорости:
F = ηS dυ/dy (формула Ньютона)
где F — абсолютное значение силы внутреннего трения, S — площадь поверхности скользящих друг по другу слоев, τ = F/S — касательное напряжение, η -множитель пропорциональности, зависящей от приводы жидкости, называемый коэффициентом внутреннего трения или динамической вязкостью, а часто и просто вязкостью. Из формулы (7) коэффициент внутреннего трения равен касательному напряжению при градиенте скорости, равном единице.
Источник