- Равноускоренное движение: формулы, примеры
- Равноускоренное движение
- Формулы для равноускоренного движения
- Закон равноускоренного движения
- Формула равноускоренного движения
- Определение и формула равноускоренного движения
- Основные кинематические величины при равноускоренном движении
- Примеры решения задач
- Равноускоренное прямолинейное движение
- Ускорение. Равноускоренное движение
- Что такое ускоренное движение
- Ускорение
Равноускоренное движение: формулы, примеры
Равноускоренное движение
Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.
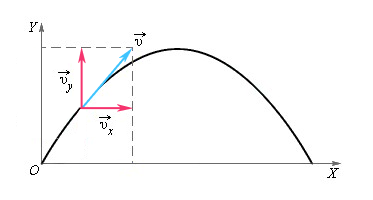
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.
В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.
Формулы для равноускоренного движения
Формула для скорости при равноускоренном движении:
Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.
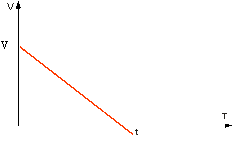
Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.
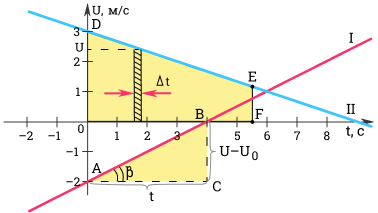
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.
a = v — v 0 t = B C A C
Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .
Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .
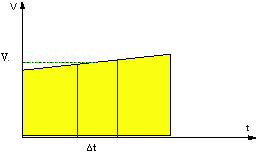
По данному графику можно также вычислить перемещение тела за время t . Как это сделать?
Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .
Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .
s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .
Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:
s = v 0 t + a t 2 2
Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Закон равноускоренного движения
y = y 0 + v 0 t + a t 2 2 .
Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s = v 2 — v 0 2 2 a .
По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:
v = v 0 2 + 2 a s .
При v 0 = 0 s = v 2 2 a и v = 2 a s
Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.
Источник
Формула равноускоренного движения
Определение и формула равноускоренного движения
Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным. Если скорость при этом увеличивается, то такое движение носит название равноускоренного движения.
Равноускоренное движение можно определить еще как движение, при котором модуль касательного ускорения ($a_<\tau>=$ const $>0$).
Основные кинематические величины при равноускоренном движении
где v2 – конечная скорость, v1— начальнаяскорость движения, t–время движения.
Скорость в любой момент равноускоренного прямолинейного движения можно найти как:
где $\bar
Уравнение для координаты материальной при равноускоренном движении записывают как:
где v0x – проекция начальной скорости на ось X, ax – проекция ускорения на ось X.
Перемещение при равноускоренном движении является функцией вида:
где $\bar_0$ – перемещение в начальный момент времени. Или $\bar$ еще можно представить как:
Примеры решения задач
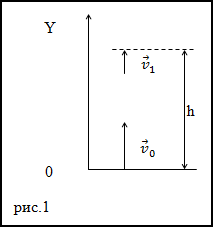
Задание. Тело было брошено вертикально вверх. Оно возвратилось на землю через промежуток времени, равный t. Какой была начальная скорость тела, и на какую высоту оно поднялось?
Решение. Тело в поле тяжести Земли движется с постоянным ускорением равным ускорению свободного падения, на рис.1 оно направлено вниз.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
Все движение происходит только по оси Y, поэтому проекция выражения (1.1) примет вид:
Формула для скорости при равноускоренном движении записывается как:
В проекции на ось она преобразуется к виду:
Точке максимального подъема мы имеем y(t1)=h и v(t1)=0 (t1 — время поъема), тогда выражения (1.2) и (1.4) перепишем как:
где $t_<1>=\frac
Подставляя выражение (1.6) вместо начальной скорости в формулу h, имеем:
Формула равноускоренного движения не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Расстояние между двумя точками равно l. Первую половину пути тело проходит равноускорено, вторую равнозамедленно. Максимальная скорость тела равна v. Каков модуль ускорения тела и время его перемещения, если ускорения на обоих участках пути равны по модулю.
Решение. Данную задачу можно решить двумя способами.
1 способ аналитический.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
Для первой половины пути, учитывая, что мы рассматриваем прямолинейное движение, запишем:
где учтено, что $\bar_<0>=0, \bar
Для второй половины пути получаем:
Суммарное время, которое провело тело в пути равно:
Наибольшая скорость движения равна:
$$v=a t_<1>=a t_ <2>\rightarrow t_<1>=t_<2>(2.5)$$
Суммарный путь равен:
Ускорение выразим из (2.2), имеем:
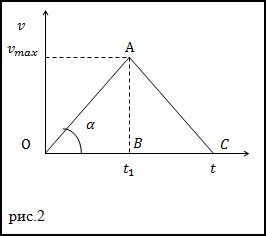
2.графический способ решения задачи.
Для этого построим график зависимости v(t).
Путь равен площади под кривой или в нашем случае сумме площадей треугольниковOABи ABC. Значит можно записать:
Ответ. $t=\frac<2 l>
Источник
Равноускоренное прямолинейное движение
Автор:– Начнем обсуждение самого простого неравномерного движения – движения с постоянным ускорением. Такое движение называют равноускоренным.
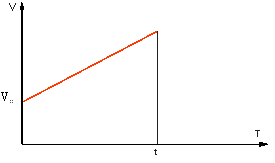
График зависимости V(t) для этого случая показан на рис.1.2.1. Промежуток времени Δt в формуле (1.4) можно брать любой. Отношение ΔV/Δt от этого не зависит. Тогда ΔV=аΔt. Применяя эту формулу к промежутку от tо = 0 до некоторого момента t, можно написать выражение для скорости:
Здесь V0 – значение скорости при tо = 0. Если направления скорости и ускорения противоположны, то говорят о равнозамедленном движении (рис. 1.2.2).
При равнозамедленном движении аналогично получаем
Разберём вывод формулы перемещения тела при равноускоренном движении. Заметим, что в этом случае перемещение и пройденный путь – одно и тоже число.
Рассмотрим малый промежуток времени Δt. Из определения средней скорости Vcp = ΔS/Δt можно найти пройденный путь ΔS = VcpΔt. На рисунке видно, что путь ΔS численно равен площади прямоугольника с шириной Δt и высотой Vcp. Если промежуток времени Δt выбрать достаточно малым, средняя скорость на интервале Δt совпадет с мгновенной скоростью в средней точке. ΔS ≈ VΔt. Это соотношение тем точнее, чем меньше Δt. Разбивая полное время движения на такие малые интервалы и учитывая, что полный путь S складывается из путей, пройденных за эти интервалы, можно убедиться, что на графике скорости он численно равен площади трапеции:
подставляя (1.5), получим для равноускоренного движения:
Для равнозамедленного движения перемещение L вычисляется так:
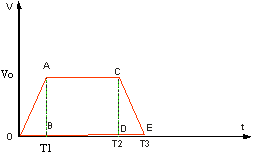
Пусть график скорости имеет вид, изображенный на рис. 1.2.4. Нарисуйте качественно синхронные графики пути и ускорения от времени.
Студент: – Мне не приходилось встречаться с понятием «синхронные графики», я также не очень представляю, что значит «нарисовать качественно».
Автор: – Синхронные графики имеют одинаковые масштабы по оси абсцисс, на которой отложено время. Расположены графики один под другим. Удобны синхронные графики для сопоставления сразу нескольких параметров в один момент времени. В этой задаче мы будем изображать движение качественно, т. е. без учета конкретных числовых значений. Для нас вполне достаточно установить: убывает функция или возрастает, какой вид она имеет, есть ли у нее разрывы или изломы и т. д. Думаю, для начала нам следует рассуждать вместе.
Разделим все время движения на три промежутка ОВ, BD, DE. Скажите, какой характер носит движение на каждом из них и по какой формуле будем вычислять пройденный путь?
Студент: – На участке ОВ тело двигалось равноускоренно с нулевой начальной скоростью, поэтому формула для пути имеет вид:
Ускорение можно найти, разделив изменение скорости, т.е. длину АВ, на промежуток времени ОВ.
Автор: – Хорошо. Теперь рассмотрите другие временные участки – ВD и DЕ.
Студент:– На участке ВD тело движется равномерно со скоростью V0, приобретенной к концу участка ОВ. Формула пути – S = Vt. Ускорения нет.
Автор: – Следует уточнить, что равномерное движение началось не в начальный момент времени, а в какой-то t1. К этому времени тело уже прошло путь at1 2 /2. Кроме того, за начало отсчета времени необходимо взять момент t1. Зависимость пути от времени имеет следующий вид:
Учитывая это пояснение, напишите формулу для пути на участке DE.
Студент:– На последнем участке движение равнозамедленное. Буду рассуждать так. До момента времени t2 тело уже прошло расстояние S2 = at1 2 /2 + V(t2– t1 ).
К нему надо добавить выражение для равнозамедленного случая, учитывая, что время отсчитывается от значения t2 получаем пройденный путь, за время t – t2:
Предвижу вопрос о том, как найти ускорение a1. Оно равно СD/DE. В итоге получаем путь, пройденный за время t>t2
Автор: – Верно. Переходите к построению графиков.
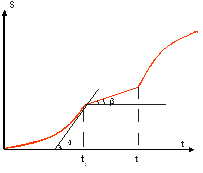
Студент:– На первом участке имеем параболу с ветвями, направленными вверх. На втором – прямую, на последнем – тоже параболу, но с ветвями вниз.
Автор:– Ваш рисунок имеет неточности. График пути не имеет изломов, т. е. параболы следует плавно сопрягать с прямой. Мы уже говорили, что скорость определяется тангенсом угла наклона касательной. По Вашему чертежу получается, что в момент t1 скорость имеет сразу два значения. Если строить касательную слева, то скорость будет численно равна tgα, а если подходить к точке справа, то скорость равна tgβ. Но в нашем случае скорость – непрерывная функция. Противоречие снимается, если график построить так.
Есть еще одно полезное соотношение между S, a, V и V0. Будем предполагать, что движение происходит в одну сторону. В этом случае перемещение тела от начальной точки совпадает с пройденным путём. Используя (1.5), выразите время t и исключите его из равенства (1.6). Так Вы получите эту формулу.
Студент:– V(t) = V0 + at , значит,
S = V0t + at 2 /2 = V0(V– V0 )/a +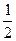 
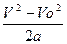
a[(V– V0 )/a] 2 = 
.
S= 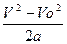. (1.6а)
Однажды во время обучения в Геттингене Нильс Бор плохо подготовился к коллоквиуму, и его выступление оказалось слабым. Бор, однако, не пал духом и в заключение с улыбкой сказал:
– Я выслушал здесь столько плохих выступлений, что прошу рассматривать моё как месть.
Источник
Ускорение. Равноускоренное движение
Что такое ускоренное движение
Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.
«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.
«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее. То есть скорость все время увеличивается.
Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, — это тоже «ускоренное» движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением .
Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 5 5 5 км/ч, потом 1 0 10 1 0 км/ч, потом 1 5 15 1 5 км/ч, 2 0 20 2 0 км/ч, 2 5 25 2 5 км/ч, 3 0 30 3 0 км/ч и т.д. — насколько у него хватит сил.
Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1 0 10 1 0 км/ч, потом 5 5 5 км/ч, а потом 0 0 0 км/ч. То есть скорость все время уменьшается на 5 5 5 км/ч.
Следуя этой логике, через мгновение после скорости в 0 0 0 км/ч скорость должна вновь уменьшиться на 5 5 5 км/ч, и тогда скорость будет равна − 5 -5 − 5 км/ч, а потом еще уменьшиться на 5 5 5 км/ч и стать уже − 1 0 -10 − 1 0 км/ч, а потом и − 1 5 -15 − 1 5 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о «стрелочке»), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы » Два вида физических величин: скалярные величины и векторные величины » и » Проектирование векторов на оси «. В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.
Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.
В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.
Ускорение
Я думаю, что вы согласитесь с тем, что разгоняться можно по-разному: можно потихонечку, а можно — резко и очень быстро. Вроде бы в обоих этих случаях движение ускоренное, но все же разное. Надо как-то различать эти два движения. Нужна численная характеристика (характеристика числом), чтобы можно было сказать, что первое движение — медленно ускоряющееся, а второе — быстро. Такая характеристика — это ускорение: a ⃗ = V ⃗ − V 0 ⃗ t , \vec=\frac<\vec
Когда говорят про равноускоренное движение, то имеют в виду, что движение происходит с ускорением, которое никогда не меняется. Равное ускорение = равноускоренное движение .
— это очень полезная для нас формула. Ее нужно запомнить.
Источник
