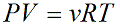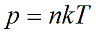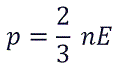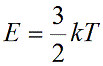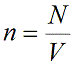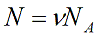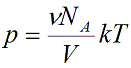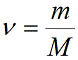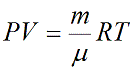Выведете уравнение менделеева клапейрона

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

ν — количество вещества [моль]

R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]

T – температура [K]

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

n — концентрация частиц [м -3 ]

k – константа Больцмана k = 1,38 · 10 -23 [Дж/К]

Т – абсолютная температура, в кельвинах [К]

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Подставим nkT вместо давления и выразим кинетическую энергию:

Концентрация частиц газа n равна:

N – число молекул газа в емкости объемом V [м 3 ]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Произведение числа Авогадро N_A и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

можно привести уравнение к следующему виду:

Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.

Закон Бойля-Мариотта — изотермический процесс

Проходит при постоянной температуре: T= const.

P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:

Закон Гей-Люссака — изобарный процесс

Проходит при постоянном давлении: P = const.

V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:

Закон Шарля — изобарный процесс

Проходит при постоянном объеме: V = const.

P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:

Понравилась статья, расскажите о ней друзьям:

Источник

Выведете уравнение менделеева клапейрона

Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V_m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT , где R — универсальная газовая постоянная,

R = 8,31 Дж/(моль . К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = N_АkT,

где N_А — число Авогадро, k — постоянная Больцмана.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P₁V₁=P₂V₂=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:

p = const => V/T = const — закон Гей — Люссака .

V= const => p/T = const — закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N_A = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N_A?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

N_A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23

PV 7,95 . 10 -4 . 3 . 10 -2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Источник

Уравнение Менделеева – Клапейрона

В резервуаре находится 10 кг азота, взятого при температуре 150 К. Найдите объем резервуара, если давление газа равно атмосферному. (Ответ дайте в м \(^3\) и округлите до сотых.)

Азот в резервуаре можно считать идеальным газом, который подчиняется уравнению Менделеева-Клапейрона: \[\hspace <5 mm>pV=\nu RT \hspace <5 mm>(1)\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа.
Количество вещества газа можно найти по формуле: \[\hspace <5 mm>\nu = \dfrac <\mu>\hspace <5 mm>(2)\] где \(m\) — масса газа, \(\mu\) — молярная масса газа.
Подставим (2) в (1): \[p V = \dfrac<\mu>RT\] Выразим объем газа: \[V=\dfrac\] Так как азот — двухатомный газ, то молярная масса равна \(\mu=2\cdot14\cdot10^<-3>\) кг/моль. \[V=\dfrac<10\text< кг>\cdot8,31\text< Дж>/(\text<моль>\cdot\text<К>)\cdot150\text< К>><10^5\text< Па>\cdot28\cdot10^<-3>\text< кг/моль>> \approx 4,45 \text< м$^3$>\]

Во сколько раз изменяется давление идеального газа при увеличении объёма идеального газа в 4 раза и увеличении его абсолютной температуры в 4 раза?

Запишем уравнение Менделеева-Клапейрона: \[pV=\nu RT\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа.
Отсюда выразим давление газа \(p\) : \[p=\dfrac<\nu RT>\] Так как температура увеличилась в 4 раза и объем увеличился в 4 раза, то давление увеличится в 1 раз.

Смесь состоит из 32 г молекулярного кислорода и 44 г углекислого газа. Найти плотность смеси при температуре 16 \(^\circ\) C и давлении 100 кПа. Ответ дайте в кг/м \(^3\) округлите до десятых.

Запишем уравнение Менделеева-Клапейрона: \[p V=\nu R T\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа.
Выразим отсюда объем смеси газов: \[\hspace <5 mm>V=\dfrac<\nu RT>

\hspace <5 mm>(1)\] Количество вещества можно найти по формуле: \[\hspace <5 mm>\nu = \dfrac<\mu>\hspace <5 mm>(2)\] где \(m\) — масса газа, \(\mu\) — молярная масса газа.
Подставим (2) в (1) с учетом того, что количество вещества смеси газов равно сумме количеств вещества кислорода и углекисого газа ( \(\nu = \nu_1 + \nu_2\) ): \[\hspace <3 mm>V=\left(\dfrac<\mu_1>+\dfrac<\mu_2>\right)\cdot\dfrac< RT>

\hspace <3 mm>(3)\] Плотность найдем по формуле: \[\hspace <5 mm>\rho=\dfrac \hspace <5 mm>(4)\] Подставим (3) в (4): \[\rho = \dfrac<\left(\dfrac<\mu_1>+\dfrac<\mu_2>\right)\cdot\dfrac< RT>

>\] \[\rho = \dfrac<0,032\text< кг>+0,044\text< кг>><\left(\dfrac<0,032\text< кг>><0,032\text< кг/моль>>+\dfrac<0,044\text< кг>><0,044\text< кг/моль>>\right)\cdot\dfrac< 8,31\text< Дж>/(\text<моль>\cdot\text<К>)\cdot(16+273)\text< К>><10^5\text< Па>>> \approx 1,6 \text< кг/м>^3\]

Газ находится в сосуде при давлении 2 МПа и температуре 27 \(^\circ\) C. После нагревания на 50 \(^\circ\) C в сосуде осталась только половина газа (по массе). Определите установившееся давление. (Ответ дайте в МПа и округлите до сотых.)

Запишем уравнение Менделеева-Клапейрона: \[p V=\nu R T\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа.
Запишем уравнение состояния газа до нагревания и после. \[p_1V=\nu_1 RT_1\] \[p_2V=\nu_2 RT_2\] Найдем отношение давления газа после нагревания к его давлению до нагревания: \[\dfrac=\dfrac<\nu_2 T_2><\nu_1 T_1>\] Выразим давление газа \(p_2\) после нагревания: \[p_2=p_1\cdot\dfrac<\nu_2 T_2><\nu_1 T_1>\] \[p_2 =2\cdot10^6\text< Па>\cdot\dfrac<1\text< моль>\cdot350\text< К>><2\text< моль>\cdot300\text< К>> \approx 1,17 \text< МПа>\]

В вертикальном цилиндре с гладкими стенками под невесомым поршнем находится \(\nu = 50\) моль газа, занимающего объём \(V = 1\) м \(^3\) при температуре \(T = 500\) К. С какой силой надо действовать на поршень перпендикулярно его поверхности, чтобы он оставался неподвижным? Атмосферное давление \(p_o = 100\) кПа , площадь поршня \(S = 20\) см \(^2\) . (Ответ дайте в ньютонах.)

Запишем уравнение Менделеева-Клапейрона: \[pV=\nu R T\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура.
Давление внутри сосуда: \[p_1=\dfrac<\nu RT>\] \[p_1=\dfrac <50\text< моль>\cdot8,31\hspace<1 mm>\text<Дж>/(\text<моль>\cdot\text<К>)\cdot500\text< К>><1\text< м>^3>=207,75 \text< кПа>\] Так как давление внутри больше атмосферного, то чтобы поршень находился в равновесии, необходимо действовать силой вниз, чтобы уравновесить силы: \[p_1S-F-p_aS=0\] \[F=p_1S-p_aS=(p_1-p_a)S\] \[F=(207,75-100)\cdot10^3\text< Па>\cdot20\cdot10^<-4>\text< м>^2=215,5 \text< Н>\]

Газ в сосуде переводится из состояния \(A\) в состояние \(B\) . Параметры, определяющие состояние идеального газа, приведены в таблице. Какое число следует внести в свободную клетку, если в ходе эксперимента объём оставался неизменным? \[\begin < | l | l | l | l | >\hline \text < Состояние >& p, 10^5 \text < Па>& \nu, \text< моль >&\hspace <0.4 cm>T, \text< К>\hspace <0.4 cm>\\ \hline \hspace<0.8 cm>A &\hspace <0,45 cm>0,8 &\hspace <0,55 cm>2 & \\ \hline \hspace<0.8 cm>B & \hspace <0,45 cm>1,2 & \hspace <0,55 cm>1 & \hspace <0,45 cm>900 \\ \hline \end\]

Запишем уравнение Менделеева-Клапейрона: \[pV=\nu R T\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа.
Выразим отсюда температуру \(T\) : \[T = \dfrac

<\nu R>\] Найдём отношение температур газа в состоянии \(A\) и состоянии \(B\) : \[\dfrac = \dfrac <\nu_A R>: \dfrac <\nu_B R>= \dfrac= \dfrac\] Отсюда выразим температуру газа \(T_A\) в состоянии \(A\) : \[T_A = T_B \cdot \dfrac = 900\text < K >\cdot \dfrac <0,8\cdot 10^5 \text< Па >\cdot 1 \text< моль >> <1,2\cdot 10^5 \text< Па >\cdot 2 \text< моль >> = 300 \text< K >\]

Газ в сосуде переводится из состояния \(A\) в состояние \(B\) . Параметры, определяющие состояние идеального газа, приведены в таблице. Какое число следует внести в свободную клетку, если в ходе эксперимента объём оставался неизменным? \[\begin < | l | l | l | l | >\hline \text < Состояние >& p, 10^5 \text < Па>& \nu, \text< моль >&\hspace <0.4 cm>T, \text< К>\hspace <0.4 cm>\\ \hline \hspace<0.8 cm>A & &\hspace <0,6 cm>2 & \hspace <0,45 cm>400 \\ \hline \hspace<0.8 cm>B & \hspace <0,45 cm>1,5 & \hspace <0,6 cm>5 & \hspace <0,45 cm>300 \\ \hline \end\]

Запишем уравнение Менделеева-Клапейрона: \[p V=\nu RT\] где \(p\) — давление газа, \(V\) — объём, \(\nu\) — количество вещества, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура.
Выразим отсюда давление \(p\) : \[p = \dfrac<\nu RT>\] Найдём отношение давлений газа в состоянии \(A\) и состоянии \(B\) : \[\dfrac =\dfrac<\nu_A R T_A> : \dfrac<\nu_B R T_B> = \dfrac<\nu_A \cdot T_A ><\nu_B \cdot T_B>\] Отсюда выразим давление газа \(p_A\) в состоянии \(A\) : \[p_A = p_B \cdot \dfrac<\nu_A \cdot T_A > <\nu_B \cdot T_B>= 1,5 \cdot 10^5 \text < Па >\cdot\dfrac <2 \text< моль >\cdot 400 \text< K >> <5 \text< моль >\cdot 300 \text< K >> = 0,8 \cdot 10^5 \text< Па >\]

Источник