Выведите формулу для холловской разности потенциалов

Эффект холла. Холловская разность потенциалов.

Эффект Холла это процесс возникновения в проводнике или полупроводнике с током помещенном в магнитное поле электрического поля которое перпендикулярно току и магнитному полю.

Для наблюдения эффекта Холла проведем такой эксперимент. Возьмем проводящую пластину прямоугольной формы. Поместим ее в постоянное магнитное поле, созданное постоянными магнитами. Далее пропустим ток через пластину подключив электроды источника тока к узким сторонам пластины. Также необходимо контролировать силу тока. Для этого между пластиной и источником тока поместим амперметр.

Если при этом к широким сторонам пластины подключить вольтметр, то мы будем наблюдать некое напряжение.

Давайте разберемся, что это за напряжение. Как известно на проводник, с током помещённый в магнитное поле действует сила Лоренца. Направление этой силы можно определить по правилу левой руки. Эта сила стремится сместить проводник с током. Но что произойдет, если проводник закреплен неподвижно. Тогда сила будет действовать на заряды, которые движутся внутри проводника. Таким образом, что они начнут смещаться к одной из широких стенок. Это будет завесить от того куда направлена сила Лоренца.

Таким образом, у одного из широких краев будет избыток зарядов, а у другого их недостача. Следовательно, на краях возникнет разность потенциалов, которая создаст поперечное электрическое поле. Когда внутренне поле уравновесит силу Лоренца, внутри наступит постоянное распределение зарядов.

Разность потенциалов, которая возникнет вследствие эффекта Холла можно представить в виде

где a ширина пластины
B магнитная индукция
Либо в такой форме

где R постоянная Холла зависящая от вещества, в котором наблюдается эффект
I ток, протекающий через материал
d толщина материала

Таким образом, можно сделать вывод, что Холловская разность потенциалов тем больше чем больше ток, протекающий через материал. Также она прямо пропорциональна магнитной индукции пронизывающей проводник. И обратно пропорционально его толщине.

Источник

Выведите формулу для холловской разности потенциалов

Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в 1879 г. американским физиком Э.Г. Холлом (1855–1938). Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.

Рассмотрим эффект, обусловленный действием лоренцевой силы на свободные заряды в проводнике. Представим себе проводник с током I в виде плоской ленты, расположенной в магнитном поле с индукцией , направленной от нас (рис. 2.19).

В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.

Это позволяет экспериментально определить знак носителя заряда в проводнике.

При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.

Подсчитаем величину холловской разности потенциалов (U_х).

Обозначим: E_x – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.

,

(2.10.1)

Перераспределение зарядов прекратится, когда сила qE_x уравновесит лоренцеву силу, т.е.

или

Плотность тока , отсюда . Тогда .

,

(2.10.2)

где – коэффициент Холла.

Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р-типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.

Из формулы (2.10.2) можно найти число носителей заряда:

,

(2.10.3)

Итак, измерение холловской разности потенциалов позволяет определить:

· знак заряда и тип носителей;

На рисунке 2.20 показана установка для исследования магнитного поля длинного соленоида с помощью датчика Холла.

Источник

Сила Лоренца. Эффект Холла

Как известно, на проводник с током в магнитном поле действует сила Ампера (1.2). Перепишем выражение для силы Ампера в несколько ином виде:

dF = I [dl,B] =jS[dl,B] =qnuS[dl,B]=qnsdl[u,B]=qndV[u,B]=qN[u,B]. (3.47)

Здесь мы учли, что I=jS; j=qnu – есть плотность тока, Sdl=dV – элемент объёма проводника, ndV=N – число электронов в этом элементе объёма. Также учли, что направления векторов uиdlсовпадают между собой, и поэтому мы имеем право в векторном произведении перенести значок вектора с элемента Idl на скорость u. Если теперь разделим обе части уравнения (3.47) на число электронов, то получим силу, действующую на движущийся электрон в магнитном поле. Эта сила называется силой Лоренца, и она равна

F = q[u,B] . (3.48)

Подчеркнём, что тот путь, которым мы получили выражение для силы Лоренца, нельзя рассматривать как вывод этой формулы. Выражение для силы Лоренца найдено экспериментально. Просто мы показали, как из одного экспериментального выражения (для силы Ампера) можно получить другое и наоборот. Но и сила Ампера и сила Лоренца представляют собой, прежде всего, экспериментально установленные законы природы. Модуль (3.48), естественно, определяется выражением

F = quBsina . (3.49)

Здесь a – угол между векторами uи B.

Так как сила Лоренца всегда перпендикулярна скорости частицы, то она работу не совершает. Она только изменяет направление скорости (оставаясь всегда перпендикулярной направлению скорости), оставляя неизменной величину скорости. Мы знаем, что движение под действием силы, всё время перпендикулярной направлению скорости и оставляющей неизменной её величину, есть движение по окружности.

Если помимо магнитного поля, имеется и электрическое, то полная сила, действующая на движущийся заряд, будет определяться как

F = q[u,B]+qE.(3.50)

Полученное выражение называют формулой Лоренца.

Можно показать, что сила магнитного взаимодействия двух движущихся со скоростью u (u

. (3.52)

Здесь – так называемая постоянная Холла. Таким образом, измеряя макрохарактеристики, такие как холловская разность потенциалов, сила тока в проводнике, индукция магнитного поля, а также поперечный размер проводника d, можно определить концентрацию зарядов и их знак – для положительных зарядов (дырок в полупроводниках), холловское поле будет иметь противоположный знак.

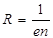
Источник

Что такое эффект Холла-полное описание,применение

Эффектом Холла называют явление возникновения поперечных разностей потенциалов (также называемых холловским напряжением) при помещении проводников с постоянным током в магнитные поля.

Если в магнитном поле с определенной индукцией разместить электронный полупроводник или проводник, по проводнику пустить электрический ток определенной плотности, то на электроны, которые передвигаются с конкретной скоростью в магнитных полях, будет действовать сила Лоренца, отклоняя их в определенную сторону.

Магнетосопротивление

Эдвин Холл проводил исследования в надежде обнаружить повышение сопротивления проводника в магнитных полях, но в слабом поле не зарегистрировал его.

Магнетосопротивление не следует из теории металлов Друде. Однако при более строгом расчёте и в сильном поле магнетосопротивление достаточно хорошо проявляется.

Квантовый эффект Холла

В сильном магнитном поле в плоских проводниках (то есть в квазидвумерных электронных газах) в системе начинает сказываться квантовый эффект, что приводит к проявлению квантового эффект Холла — квантованию холловского сопротивления.

В сильном магнитном поле появляется дробный квантовый эффект Холла, с которым связана кардинальная перестройка внутренней структуры двумерных электронных жидкостей.

Аномальный эффект Холла

Пример возникновения напряжения в образцах, перпендикулярного направлению пропускаемых токов через образец, наблюдающегося в отсутствие приложенных постоянных магнитных полей. Явление полностью совпадает с эффектом Холла, но наблюдается без внешних постоянных магнитных полей.

Для наблюдения аномального эффекта необходимо нарушение инвариантности в отношении обращения времени в системе. Аномальный эффект Холла нередко наблюдаться в образце с намагниченностью.

Спиновый эффект Холла

В случаях отсутствия магнитных полей в немагнитном проводнике могут наблюдаться отклонения носителя тока в разные стороны с противоположным направлением спинов перпендикулярно электрическим полям.

Подобное явление получило определение спинового эффекта Холла, было предсказано теоретически Перелем и Дьяконовым в 1971 году. Говорят о внешних и внутренних спиновых эффектах. Внешние связаны со спин-зависимым рассеянием, а внутренние — со спин-орбитальным взаимодействием.

Применение

Датчики Холла используются для измерения силы постоянного тока в проводниках.

Эффект Холла допускает определение концентрации и подвижности носителей зарядов, а в некоторых случаях и типы носителей зарядов (дырки или электроны) в металлах или полупроводниках, что делает его хорошим методом изучения свойств полупроводников.

На основе эффекта Холла работает датчик Холла — прибор, измеряющий напряжённость магнитных полей.

Датчик Холла получил большое распространение в вентильных или бесколлекторных электродвигателях (сервомоторах).

Датчик закрепляется непосредственно на статорах двигателей и выступает в роли ДПР или датчика положения ротора. ДПР создает обратную связь по положениям ротора, выполняет те же действия, что и коллекторы в коллекторном ДПР.

На базе принципов действия эффекта Холла активно работают некоторые варианты реактивных ионных двигателей. Устройства на базе эффекта Холла довольно часто применяются в технологиях изготовления смартфонов, как физическая основа работы электронных компасов.

Источник

Выведите формулу для холловской разности потенциалов

Лабораторная работа № 405.

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ НОСИТЕЛЕЙ ТОКА В ПОЛУПРОВОДНИКЕ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА

Цель работы : 1) определение постоянной Холла;

2) определение концентрации носителей заряда.

Приборы и принадлежности: установка для изучения эффекта Холла, образец (датчик Холла), источник питания образца, цифровые вольтметры.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Более века тому назад (1879г.) американский физик Холл, поместив тонкую золотую пластинку в магнитное поле, обнаружил, что при протекании по ней электрического тока в направлении, поперечном вектору магнитной индукции и вектору плотности тока, появляется электрическое поле. Этот эффект впоследствии был назван эффектом Холла, а поперечное электрическое поле – полем Холла.

Эффект Холла непосредственно связан с подвижностью и концентрацией носителей заряда, а знак ЭДС Холла зависит от знака заряда. Поэтому эффект Холла широко применяется при исследовании электрических свойств различных материалов и для контроля качества полупроводниковых материалов, идущих на изготовление приборов.

Изучение температурной зависимости эффекта Холла дает важную информацию о механизмах рассеяния [1] носителей заряда, о ширине запрещенной зоны материала и энергии ионизации различных примесей.

Весьма широкое применение эффект Холла находит в современной технике, являясь основой для создания приборов различного назначения: магнитометров, преобразователей постоянного тока в переменный и переменного в постоянный, усилителей постоянного и переменного тока, микрофонов, приборов автоматики и контроля, элементов вычислительной техники и многого другого.

Эффект Холла является прямой демонстрацией действия силы Лоренца на движущиеся электрические заряды.

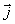
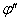
Рассмотрим проводник (или полупроводник) в виде параллелепипеда шириной а и толщиной d , через который протекает электрический ток плотностью , как показано на рис.1. Предположим также, что в проводнике имеются носители заряда одного знака: либо электроны, либо дырки. Проведем рассмотрение электронного проводника. Выберем на гранях, параллельных току, точки А и D , лежащие на одной эквипотенциальной поверхности [2] . Напряжение между этими точками U_x = 0.

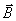
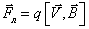
Поместим проводник в магнитное поле, вектор индукции которого перпендикулярен направлению тока и боковым граням. Под действием силы Лоренца

электроны отклоняются к передней (по рисунку) грани образца, заряжая ее отрицательно. На противоположной грани образца накапливаются нескомпенсированные положительные заряды. Это приводит к появлению электрического поля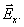

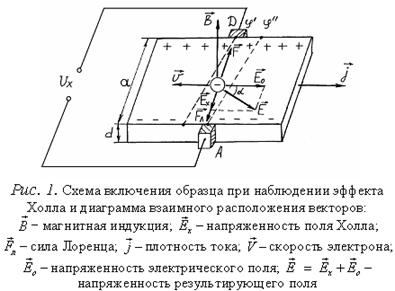
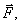
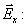
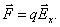
Смещение и разделение зарядов будет продолжаться до тех пор, пока сила Лоренца не уравновесится силой действующей на электроны со стороны поля Холла

Сила, действующая на электрон в условиях динамического равновесия, равна

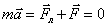
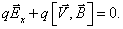
Отсюда поле Холла

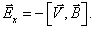
Результирующее электрическое поле

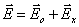
повернется при этом на угол Холла a , определяемый выражением

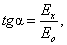
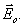
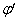
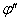
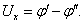
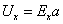
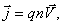
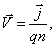
относительно вектора Соответственно эквипотенциальные поверхности и тоже изменят свое положение, и точки А и D в результате окажутся на разных эквипотенциальных поверхностях и между ними появится напряжение (ЭДС Холла):

и то есть

то можно записать, что

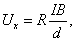
где учтено, что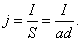

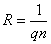
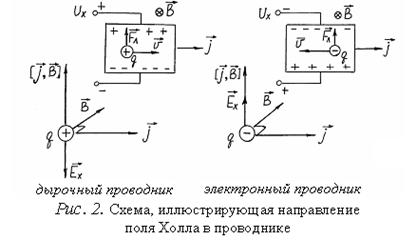
Величина называется постоянной Холла. Знак постоянной Холла зависит от знака заряда и определяет направление поля Холла ( рис.2). У электронных полупроводников (полупроводников n —типа) R имеет отрицательный знак, у дырочных (полупроводников р-типа) – положительный.

Таким образом, определяя постоянную Холла и ее знак, можно определить концентрацию и знак носителей тока в полупроводнике.

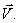
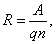
Рассмотренная модель эффекта Холла применима для проводников (металлов) и вырожденных полупроводников [3] , т.е. к проводникам, в которых имеются носители одного знака, обладающие одинаковой скоростью В невырожденных полупроводниках скорость носителей подчиняется распределению Максвелла. Учет этого обстоятельства приводит к формуле

где А – постоянная, зависящая от механизма рассеяния носителей.

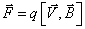
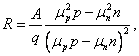
В полупроводниках со смешанной проводимостью перенос тока осуществляется одновременно электронами и дырками. Так как они обладают противоположными по знаку зарядами и под действием внешнего поля перемещаются в противоположные стороны, то сила Лоренца отклоняет их в одну и ту же сторону. Поэтому при прочих равных условиях ЭДС Холла и постоянная Холла у таких проводников меньше, чем у проводников с одним типом носителей. Расчет показывает, что для таких проводников

где n и р – концентрации электронов и дырок, m _n и m _р – их подвижности.

В зависимости от того, какое из слагаемых числителя больше, знак Холла может быть положительным или отрицательным. Для собственных полупроводников, у которых концентрации электронов и дырок одинаковы, знак постоянной Холла определяется знаком носителей, имеющих более высокую подвижность. Обычно такими носителями являются электроны. Поэтому в примесном дырочном полупроводнике (полупроводнике р-типа) при повышении температуры и переходе к собственной проводимости постоянная Холла проходит через нуль и меняет знак.

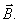
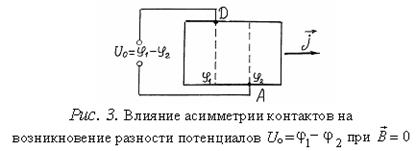
При измерении постоянной Холла и напряжения Холла следует иметь ввиду, что между холловскими электродами А и D имеется некоторая разность потенциалов U _о и в отсутствии магнитного поля Эта разность потенциалов обусловлена асимметрией контактов (на практике очень трудно расположить их на одной эквипотенциальной поверхности, см. рис.3), и термоэдс, связанной с неизотермичностью образца. Для исключения влияния начальной разности потенциалов U _о на результаты измерения можно воспользоваться следующим методическим приемом.

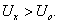
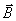
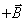
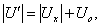
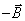
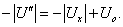
При изменении направления магнитного поля на обратное знак ЭДС Холла U _х изменится, в то время как знак U _о остается прежним. При этом в зависимости от соотношения величин U _х и U _о возможны два подхода к определению U _х . Чаще встречается случай, когда Тогда для различных направлений (условно обозначенных ниже знаками + и — ) измеряемое напряжение U меняет свой знак, и можно записать:

Вычитая из первого уравнения второе, получим

(1)

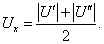
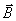
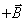
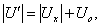
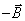
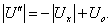
Если U _х U _о , тогда при различных направлениях знак измеряемого напряжения не изменяется и можно записать

Вычитая из первого уравнения второе, получим

(2)

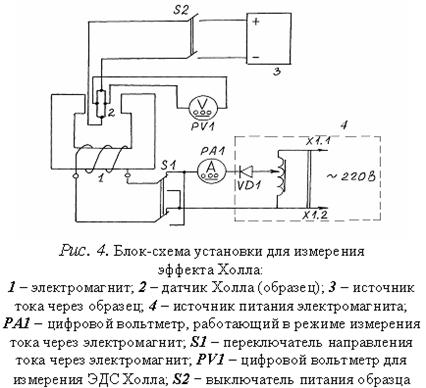
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ

Установка состоит из трех основных частей: 1) – электромагнит со схемой питания; 2) – схема питания датчика Холла; 3) – измерительная часть для определения знака и величины ЭДС Холла.

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА

1. Включить источник питания электромагнита 4.

2. Включить источник тока 3 через образец. Ток, протекающий через образец I = 35 мА.

3. Провести измерения холловской разности потенциалов, меняя величину тока I _э, текущего через электромагнит с шагом примерно 0,02 А в интервале от 0,02 до 0,12 А. Величина тока электромагнита регулируется лабораторным автотрансформатором, включенным в цепь питания электромагнита и измеряется цифровым вольтметром РА1, работающим в режиме измерения силы тока.

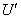
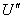
Измерения холловской разности потенциалов при каждом установленном значении тока I , выполнять при двух направлениях тока (одному направлению соответствует значение напряжения , другому — ). Направление тока изменяется переключателем S 1, установленным на лицевой панели прибора. Результаты измерений и занести в таблицу.

Источник