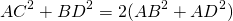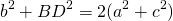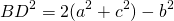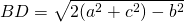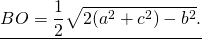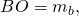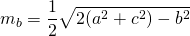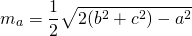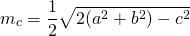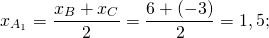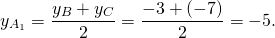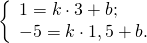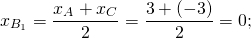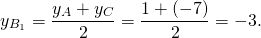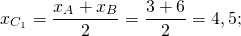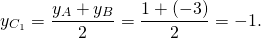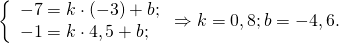Выведите формулу для медианы треугольника

По сторонам треугольника найти его медиану

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

Дано: ∆ ABC,

сторона AC — наибольшая,

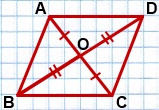
1) На луче BO отложим отрезок OD, OD=BO.

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

так как BO=1/2 BD (по построению),

Если ввести обозначение

формула для нахождения медианы треугольника по его сторонам примет вид:

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Источник

Теорема косинусов. Следствия из теоремы косинусов. 9-й класс

Класс: 9

Тип урока: Урок – семинар.

Вид урока: Урок формирования умений и навыков, применения теоремы косинусов, ее следствий при решении задач и доказательства теорем.

• Образовательные:
  1. Совершенствовать навыки решения задач с использованием теоремы косинусов и ее следствий.
  2. Вывести формулу о медиане треугольника и показать применение этой формулы при решении задач.
  3. Ознакомить учащихся с методом дополнительных построений при выводе формул и при решении задач.
• Развивающая:
  1. Формирование и совершенствование умений обобщать путем сравнения, постановка и решение проблем, рассуждение по аналогии, оперирование уже знакомыми геометрическими понятиями и фактами.
  2. Развивать психологические характеристики личности учащихся: выдвижению гипотез, формированию проблем.
  3. Развивать психические свойства: память, воображение.
• Воспитательные:
  1. Отрабатывать навыки устной речи.
  2. Воспитывать умение слушать друг друга и учителя.

1. Организационный момент.

• Приветствие.
• Сегодня мы с вами продолжим работу по теме : “Теорема косинусов и ее следствия”. Используя метод дополнительного построения, выведем формулы для вычисления медиан треугольника и применим ее при решении задач.

2. Проверка домашнего задания.

• Устно формулируем теорему косинусов, ее следствия.
• Анализируем ответы и этапы решения домашних задач.

Определите вид треугольника заданного своими сторонами 17, 8,15.

Наибольший угол лежит против стороны, равной 17, то по следствию из теоремы косинусов:

Ответ: треугольник прямоугольный.

Найдите сторону АВ в треугольнике АВС,

Найдите сторону АС равнобедренного треугольника АВС , если АВ=ВС=4 и медиана АД равна 3.

3. Вывод формулы для вычисления медианы треугольника, если известны все стороны треугольника.

Найдите медиану треугольника АВС с известными сторонами а,в,с.

Отложим отрезок ДК на продолжении медианы ВД, равный ВД. Соединим точки А, К и С,К. Получившийся четырехугольник параллелограмм по признаку( диагонали четырехугольника пересекаются и точкой пересечения делятся пополам).

Применим следствие из теоремы косинусов для параллелограмма:

ВК 2 + АС 2 = 2АВ 2 + 2ВС 2

Значит, (2m_в) 2 + в 2 = 2с 2 + 2а 2 или 4m_в 2 = 2с 2 + 2а 2 – в 2

Запишем аналогичные формулы, для медиан проведенные к другим сторонам:

Решим домашнюю задачу с использованием этой формулы.

Делаем вывод о том, какое решение рациональней.

4. Вопрос: Можно ли найти сторону треугольника, если известны все ее медианы? Выведем формулу для вычисления стороны треугольника по ее медианам. Для этого воспользуемся опять дополнительным построением.

Учащийся у доски выводит формулу.

– Какое дополнительное построение будем проводить?

– Какую фигуру получили и почему?

– Какую теорему будем применять?

Применим следствие из теоремы косинусов для параллелограмма АОСО₁:

Аналогично для других сторон :

Зная метод вывода формулы, всегда можно ее получить.
Применим эту формулу для решения задач. Учащиеся самостоятельно решают, затем проверка на доске.

№ 1 В треугольнике АВС сторона АС равна 20, а медианы , проведенные к другим сторонам равны 18 и 24 соответственно. Найдите третью медиану треугольника.

Метод дополнительного построения используется и при решении задач.

№ 2 Найдите площадь остроугольного треугольника АВС,

5. Подведение итогов урока:

• Какие новые формулы изучили на уроке?
• Какой метод применяли для доказательства теорем и решения задач?

6. Домашнее задание:

1. Найдите площадь треугольника, если две стороны его соответственно равны 27 и 29, а медиана проведенная к третьей стороне равна 26.
2. Найдите площадь остроугольного треугольника АВС,

Математика, правильно понятая, обладает не только истинной, но так же величайшей красотой.
Бертран Рёссель

Источник

Как вывести формулу медианы треугольника

Медиана в треугольнике – это отрезок, который проводят из вершины угла к середине противоположной стороны. Чтобы найти длину медианы, необходимо воспользоваться формулойвыражения ее через все стороны треугольника, которую нетрудно вывести.

Чтобы вывести формулу для медианы в произвольном треугольнике, необходимо обратиться к следствию из теоремы косинусов для параллелограмма, получающегося путем достраивания треугольника. Формулу можно доказать на этом основании, она очень удобна при решении задач, если известны все длины сторон или их легко можно найти из других начальных данных задачи.

Фактически теорема косинусов представляет собой обобщение теоремы Пифагора. Она звучит так: для двумерного треугольника с длинами сторон a, b и c и углом α, противолежащим стороне a, справедливо следующее равенство:a² = b² + c² – 2•b•c•cos α.

Обобщающее следствие из теоремы косинусов определяет одно из важнейших свойств четырехугольника: сумма квадратов диагоналей равна сумме квадратов всех его сторон: d1² + d2² = a² + b² + c² + d².

Решите задачу: пусть в произвольном треугольнике ABC известны все стороны, найдите его медиану BM.

Достройте треугольник до параллелограмма ABCD добавлением линий, параллельных a и c. таким образом, сформировалась фигура со сторонами a и c и диагональю b. Удобнее всего строить так: отложите на продолжении прямой, которой принадлежит медиана, отрезок MD той же длины, соедините его вершину с вершинами оставшихся двух сторон A и C.

По свойству параллелограмма диагонали делятся точкой пересечения на равные части. Примените следствие из теоремы косинусов, согласно которому сумма квадратов диагоналей параллелограмма равна сумме удвоенных квадратов его сторон:BK² + AC² = 2•AB² + 2•BC².

Поскольку BK = 2•BM, а BM – это медиана m, то:(2•m) ² + b² = 2•c² + 2•a², откуда:m = 1/2•√(2•c² + 2•a² — b²).

Вы вывели формулу одной из медиан треугольника для стороны b: mb = m. Аналогично находятся медианы двух других его сторон:ma = 1/2•√(2•c² + 2•b² — a²);mc = 1/2•√(2•a² + 2•b² — c²).

Источник

Уравнение медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Источник