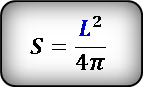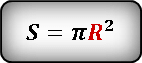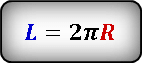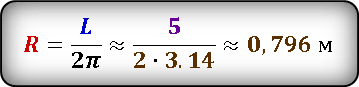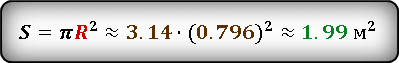Выведите формулу для вычисления площади круга

Выведите формулу для вычисления площади круга?

Геометрия | 5 — 9 классы

Выведите формулу для вычисления площади круга.

Sкруга = П(пи — 3, 14) * R(радиус).

Выведите формулу для вычисления суммы углов выпуклого n — угольника?

Выведите формулу для вычисления суммы углов выпуклого n — угольника.

Формулы длины окружности и площади круга?

Формулы длины окружности и площади круга?

Запишите формулу Герона для вычисления площади треугольника по трём сторонам?

Запишите формулу Герона для вычисления площади треугольника по трём сторонам.

Выведите формулу для вычисления координат середины отрезка по координатам его концов?

Выведите формулу для вычисления координат середины отрезка по координатам его концов.

Ребят, help me, please?

Ребят, help me, please!

Выведите формулу для вычисления площади треугольника по радиусу вписанной окружности r и полупериметру p : SΔ = r * p.

Прошу не писать формулу, она уже есть!

Ее нужно вывести.

Заранее огромное спасибо!

Записать формулу для вычисление площади ромба?

Записать формулу для вычисление площади ромба.

Выведите формулу для вычисления расстояния между двумя точками по их координатам?

Выведите формулу для вычисления расстояния между двумя точками по их координатам.

1) Выведите формулу площади трапеции?

1) Выведите формулу площади трапеции.

2) Найдите площадь прямоугольного треугольника, катеты которого 10 и 7 см.

Формулу вычисления площади у треугольника, пожалуйста?

Формулу вычисления площади у треугольника, пожалуйста.

Формула площади круга, вычисление радиуса?

Формула площади круга, вычисление радиуса.

Вы открыли страницу вопроса Выведите формулу для вычисления площади круга?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Да может вариант ответа б.

Углы квадрата равны 90°. ∠СВК = 90° — 60° = 30° СК = ВС• tg 30° = √6 : √3 = √2 Катет СК противолежит углу 30°, ⇒ гипотенуза ∆ СВК сторона ВК = 2 СК = 2 √2 Стороны квадрата равны. По т. Косинусов АК² = АВ² + ВК² — 2 АВ•ВК• cos60° АК² = 6 + 8 — 2 √6..

Параллельные прямые это прямые которые не пересекаются, а по рисунку видно , что 2 прямые пересекаются , а значит они не параллельны.

Да могу : потому что D и B поролельна сторона.

Вот решение на твою задачу.

По теореме Пифагора ab = 64 + 36 = 100 ab = 100 под корнем ab = 10.

А) Перпендикуляр из B на AD попадает в середину E отрезка AD (следует из равнобедренности треугольника ABD). По той же причине перпендикуляр из C на AD попадает в ту же точку E. Значит, вся прямая BC лежит в плоскости, перпендикулярной AD⇒ BC⊥AD. ..

Угол 2 односторонний с углом 65° следовательно он равен 180 — 65 = 115° Угол 1 и угол 3 смежные с углом 2 значит 180 — 115 = 65°.

MN = MK как касательные к окружности, проведённые из одной точки. Пусть прямая АВ касается окружности в точке Н. AN = AH и ВК = ВН как касательные. Р(ΔМАВ) = МА + МВ + АН + ВН = МА + МВ + AN + BK = MN + MK, значит МN = МК = Р(ΔМАВ) / 2 = 48 / 2 = ..

Сначала найдем гипотенузу : Теперь выразим площади этого треугольник через высоту и через катеты : а, b — катеты треугольника c — гипотенуза треугольника h — высота треугольника.

Источник

Формула площади круга через диаметр или радиус или длину окружности.

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

или радиус круга или длину окружности, можно найти его площадь.

r — радиус круга

D — диаметр круга

Формула площади круга, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через радиус

Калькулятор для расчета площади круга через диаметр

L — длина окружности

О — центр круга

Формула площади круга если известна длина окружности, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через длину

Источник

Задача: определить площадь круга, если известна длина окружности

Условие задачи:

Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.

Дано:
Длина окружности, L = 5 м

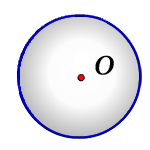
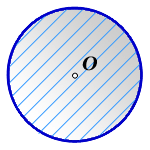
Пояснение к рисунку:
O — центр окружности

Найти площадь круга: S

Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.

Определить радиус, нам поможет формула длины окружности.

После преобразования, выразим радиус через длину окружности и подставим значения.

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Получили значение радиуса окружности.

В формулу площади круга, подставляем найденное значение радиуса.

Ответ:

Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение

Источник

выведите формулу для вычисления площади круга. геометрия.

S круга = П(пи-3,14)* R(радиус)

S= пR в квадрате
R=радиусу круга

Другие вопросы из категории

Читайте также

5. Выведите формулу для вычисления площади правильного
многоугольника через его периметр и радиус вписанной
окружности.
6.Выведите формулы для вычисления стороны правильного
я-угольника и радиуса вписанной в него окружности через
радиус описанной окружности.
7. Как выражаются стороны правильного треугольника,

Прошу не писать формулу, она уже есть! Ее нужно вывести. Заранее огромное спасибо!

2. Вычислите площадь поверхности и объем куба с длиной стороны 3 см? (решение и ответ).

3. Длина ребра куба равна k. Запишите формулы для вычисления площади его поверхности S и V?

4. Объем куба равен 1000 дм куб. Определите длину его ребра способом подбора? (решение и ответ).

5. Площадь основания прямоугольного параллелепипеда равна 50 см кв., а высота 40 см. Вычислите объем параллелепипеда? (решение и ответ).

6. Вырази в указанных единицах: 12 000 дм куб. = в м куб. и 24 см куб. = в мм куб.?

данным векторам. 3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам. 4)Объясните, как вводится прямоугольная системы координат. 5)Что такое координатные векторы? 6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам. 7)Что такое координаты вектора? 8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.9)Что такое радиус-вектора точки?Докажите, что координаты точки равны соответствующим координатам векторов. 10)Выведите формулы для вычисления координат вектора по координатам его начала и конца. 11)Выведите формулы для вычисления координат вектора по координатам его концов. 12) Выведите формулу для вычисления длины вектора по его координатам. 13)Выведите формулу для вычисления расстояния между двумя точками по их координатам. 14)Приведите пример решения геометрической задачи с применением метода координат. 15)Какое уравнение называется уравнением данной линии?Приведите пример. 16)Выведите уравнение окружности данного радиуса с центром в данной точке. 17)Напишите уравнение окружности данного радиуса с центром в начале координат. 18)Выведите уравнение данной прямой в прямоугольной системе координат. 19)Напишите уравнение прямых, проходящих через данную точку M0 (X0 : Y0) и параллельных осям координат. 20)Напишите уравнение осей координат. 21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.

формулы для вычисления площади треугольника

5) вывод формулы для вычисления площади трапеции

6) вывод значений синуса косинуса и тангенса углов равных 30 и 60 45 градусов

Источник

Площадь круга – формулы, примеры расчетов

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Окружность и круг — в чём отличие?

Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.

Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.

Площади фигур

Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур). Площади фигур

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

<	x = a + r cos t
	y = b + r sin t

Найти площадь кругаОнлайн калькулятор

Радиус круга r

Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Формула площади круга через диаметр

• S=π*d 2 /4, где
• S – площадь круга
• π – постоянное число, равное 3,14
• d – диаметр окружности

Формула площади круга через радиус

Таблица с формулами площади круга

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	радиус
2	диаметр
3	длина окружности
4	сторона квадрата вписанного в круг
5	сторона квадрата, в который вписан круг
6	стороны треугольника
7	сторона равностороннего треугольника
8	высота равностороннего треугольника
9	боковая сторона и основание равнобедренного треугольника
10	стороны при прямом угле треугольника
11	боковая сторона и основание равнобедренного треугольника
12	боковые стороны равнобедренного треугольника и угол между ними
13	стороны прямоугольного треугольника
14	сторона и угол при основании треугольника
15	сторона равностороннего треугольника
16	сторона и угол при основании трапеции
17	боковые стороны и диагональ трапеции
18	стороны прямоугольника
19	сторона и количество сторон многоугольника
20	сторона шестиугольника

Длина окружности круга

Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π , как отношение длины окружности C к двум ее радиусам r . Исходя из этого, выводится формула длины окружности C , которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r .

Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r =2 см.

Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.

Центральный угол, вписанный угол и их свойства

Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Источник