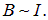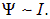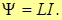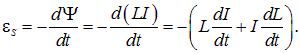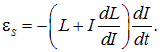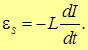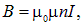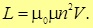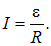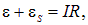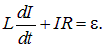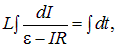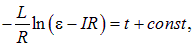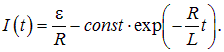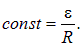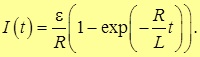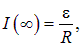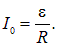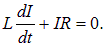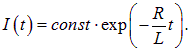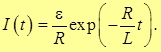Выведите формулу эдс самоиндукции

8.3. Явление самоиндукции

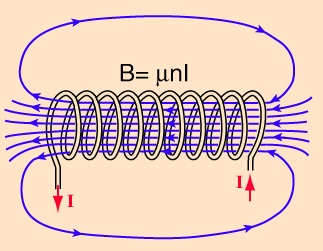
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока

Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре

Введем коэффициент пропорциональности L

Коэффициент пропорциональности L называется индуктивностью контура.

Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока.

Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.

В системе СИ единицей измерения индуктивности является генри (Гн)

Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.

Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

Видео 8.13. Закон Фарадея. Явление самоиндукции.

Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.

Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.

Выведем формулу для ЭДС самоиндукции 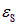. Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени

Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков

,

что необходимо учитывать при дифференцировании

Подставляя это выражение в (8.17), получаем для неподвижного контура всреде

Если же индуктивность контура не зависит от силы тока в нём, то имеем

Мы приходим к закону самоиндукции. В этом простейшем случае:

В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи.

Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна

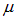
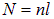
где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как

где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между 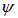и I, получаем величину индуктивности длинного соленоида (рис. 8.31)

Рис. 8.31. Индуктивность соленоида

При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.

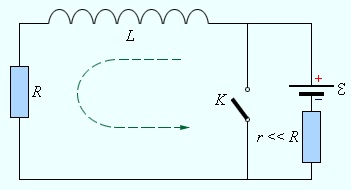
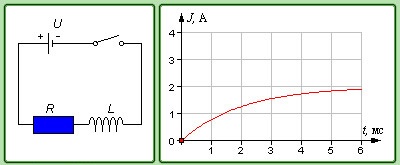
Рассмотрим цепь, состоящую из сопротивления, индуктивности и источника тока (рис. 8.32).

Рис. 8.32. Цепь, содержащая катушку, сопротивлении и источник постоянного тока

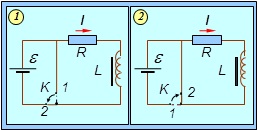
Рис. 8.33. Токи замыкания (1) и размыкания (2) цепи с индуктивностью

Будем считать, что в сопротивление R уже включены соединенные с ним последовательно внутреннее сопротивление источника и сопротивление катушки. После того, как исчезнут экстра токи замыкания и размыкания и установится постоянный ток, сила тока в цепях, показанных на рис. 8.33, согласно закону Ома, будет равна

При разомкнутомключе ток не идет. Что будет, если ключ замкнуть, перебросив его из положения 1 в положение 2?

Обозначим через I мгновенное значение силы тока в цепи: 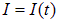(функция времени). Если учесть ЭДС самоиндукции, то в каждый момент времени по-прежнему справедлив закон Ома

Подставим в (8.22) выражение (8.19), предполагая, что индуктивность не зависит от тока. В результате применения закона Ома получаемдифференциальное уравнение для силы тока в цепи

Это уравнение легко интегрируется

откуда следует общее решение уравнения (8.23)

Постоянную интегрирования сonst определяем из начального условия: в момент времени t = 0 (замыкание ключа) тока в цепи еще не было, то есть I(0) = 0. Тогда

Таким образом, зависимость от времени тока замыкания в цепи с индуктивностью имеет вид

имеет размерность времени и является характерным временем нарастания тока в цепи с индуктивностью. Сначала ток растет от нулевого значения линейно, затем скорость его роста начинает уменьшаться и ток асимптотически стремится к своему предельному значению

равному току в этой же цепи в отсутствие индуктивности. Практически предельное значение тока, учитывая реальную точность измерений силы тока, достигается за времена примерно равные 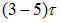(рис. 8.34).

Рис. 8.34. Ток замыкания цепи с индуктивностью

Рассмотрим теперь рис. 8.33-2. Сначала ключ находился в положении 1, и в цепи шел ток

При перебрасывании ключа в положение2 источник тока отключается от цепи, и ток I начинает уменьшаться. Закон Ома для замкнутого участка цепи имеет теперь вид

В отличие от (8.23) в разомкнутой цепи больше нет ЭДС 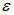и действует только ЭДС самоиндукции. Уравнение (8.26) интегрируется еще легче

Учитывая, что начальный ток в цепи был равен

для зависимости от времени тока размыкания в цепи с индуктивностью получаем

На рис 8.35 представлен опыт, иллюстрирующий явления при замыкании и размыкании цепи, содержащей индуктивность. В цепь питания большой катушки индуктивности включена электрическая лампа. При замыкании цепи ключом лампа загорается не сразу, поскольку ЭДС самоиндукции препятствует изменению тока (правило Э.Х. Ленца). При размыкании наблюдается яркая вспышка из-за того, что источником тока становится ЭДС самоиндукции катушки, которая при резком изменении силы тока обычно заметно больше ЭДС источника.

Рис. 8.35. Явления при замыкании и размыкании цепи, содержащей индуктивность

Видео 8.14. Явление самоиндукции. Токи при замыкании и размыкании цепи.

Пример. К источнику с внутренним сопротивлением 2 Ом подключают катушку индуктивностью 0,5 Гн и сопротивлением 8 Ом. Найти время T, в течение которого после замыкания цепи ток в катушке достигнет значения, отличающегося от максимального на .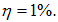

Решение. В этой задаче полное сопротивление цепи равно

где r — внутреннее сопротивление источника, а 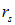— сопротивление катушки. Согласно (8.25), ток в момент времени Т равен

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Индуктивность

Электрический ток, проходящий по контуру, создает вокруг него магнитное поле. Магнитный поток Φ через контур этого проводника (его называют собственным магнитным потоком) пропорционален модулю индукции В магнитного поля внутри контура \(\left( \Phi \sim B \right)\), а индукция магнитного поля в свою очередь пропорциональна силе тока в контуре \(\left( B\sim I \right)\).

Таким образом, собственный магнитный поток прямо пропорционален силе тока в контуре \(\left( \Phi \sim I \right)\). Эту зависимость математически можно представить следующим образом:

где L — коэффициент пропорциональности, который называется индуктивностью контура.

• Индуктивность контура — скалярная физическая величина, численно равная отношению собственного магнитного потока, пронизывающего контур, к силе тока в нем:

\(

В СИ единицей индуктивности является генри (Гн):

1 Гн = 1 Вб/(1 А).

• Индуктивность контура равна 1 Гн, если при силе постоянного тока 1 А магнитный поток через контур равен 1 Вб.

Индуктивность контура зависит от размеров и формы контура, от магнитных свойств среды, в которой находится контур, но не зависит от силы тока в проводнике. Так, индуктивность соленоида можно рассчитать по формуле

L = \mu \cdot \mu_0 \cdot N^2 \cdot \dfrac,\)

где μ — магнитная проницаемость сердечника, μ₀ — магнитная постоянная, N — число витков соленоида, S — площадь витка, l — длина соленоида.

При неизменных форме и размерах неподвижного контура собственный магнитный поток через этот контур может изменяться только при изменении силы тока в нем, т.е.

\(\Delta \Phi =L \cdot \Delta I.\) (1)

Явление самоиндукции

Если в контуре проходит постоянный ток, то вокруг контура существует постоянное магнитное поле, и собственный магнитный поток, пронизывающий контур, не изменяется с течением времени.

Если же ток, проходящий в контуре, будет изменяться со временем, то соответственно изменяющийся собственный магнитный поток, и, согласно закону электромагнитной индукции, создает в контуре ЭДС.

• Возникновение ЭДС индукции в контуре, которое вызвано изменением силы тока в этом контуре, называют явлением самоиндукции. Самоиндукция была открыта американским физиком Дж. Генри в 1832 г.

Появляющуюся при этом ЭДС — ЭДС самоиндукции E_si. ЭДС самоиндукции создает в контуре ток самоиндукции I_si.

Направление тока самоиндукции определяется по правилу Ленца: ток самоиндукции всегда направлен так, что он противодействует изменению основного тока. Если основной ток возрастает, то ток самоиндукции направлен против направления основного тока, если уменьшается, то направления основного тока и тока самоиндукции совпадают.

Используя закон электромагнитной индукции для контура индуктивностью L и уравнение (1), получаем выражение для ЭДС самоиндукции:

\(E_ =-\dfrac<\Delta \Phi ><\Delta t>=-L\cdot \dfrac<\Delta I><\Delta t>.\)

• ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в контуре, взятой с противоположным знаком. Эту формулу можно применять только при равномерном изменении силы тока. При увеличении тока (ΔI > 0), ЭДС отрицательная (E_si При уменьшении тока (ΔI 0), т.е. индукционный ток направлен в ту же сторону, что и ток источника.

Из полученной формулы следует, что

\(L=-E_ \cdot \dfrac<\Delta t><\Delta I>.\)

• Индуктивность – это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Явление самоиндукции можно наблюдать на простых опытах. На рисунке 1 показана схема параллельного включения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L. При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. Объясняется это тем, что на участке цепи с лампой 1 нет индуктивности, поэтому тока самоиндукции не будет, и сила тока в этой лампе почти мгновенно достигает максимального значения. На участке с лампой 2 при увеличении тока в цепи (от нуля до максимального) появляется ток самоиндукции I_si, который препятствует быстрому увеличению тока в лампе. На рисунке 2 изображен примерный график изменения тока в лампе 2 при замыкании цепи.

Источник

Читайте также:  Маркер для тетрадей пиши стирай