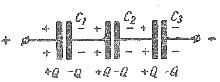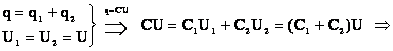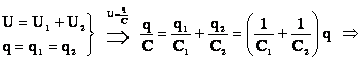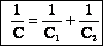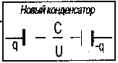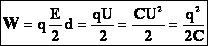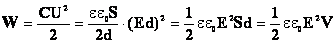Параллельное и последовательное соединение конденсаторов

Отдельные конденсаторы могут быть соединены друг с другом различным образом. При этом во всех случаях можно найти емкость некоторого равнозначного конденсатора, который может заменить ряд соединенных между собой конденсаторов.

Для равнозначного конденсатора выполняется условие: если подводимое к обкладкам равнозначного конденсатора напряжение равно напряжению, подводимому к крайним зажимам группы конденсаторов, то равнозначный конденсатор накопит такой же заряд, как и группа конденсаторов.

Параллельное соединение конденсаторов

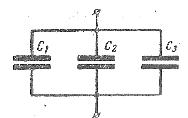
На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U , Q 2 = C 2 U , Q 3 = C 3 U , а заряд, полученный от источника Q = Q1 + Q2 + Q3.

Рис. 1. Схема параллельного соединения конденсаторов

Общая емкость равнозначного (эквивалентного) конденсатора:

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3 ,

т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.

Последовательное соединение конденсаторов

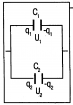
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q

Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.

Рис. 3. Схема последовательного соединения конденсаторов

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1 , U1 = Q/C 2, U1 = Q/C 3, а общее напряжение U = U1 + U2 + U3

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / ( U1 + U2 + U3 ), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.

Пример 1 . Три конденсатора, емкости которых C1 = 20 мкф, С2 = 25 мкф и С3 = 30 мкф, соединяются последовательно, необходимо определить общую емкость.

Общая емкость определяется из выражения 1/С = 1/С1 + 1/С2 + 1/С3 = 1/20 + 1/25 + 1/30 = 37/300, откуда С = 8,11 мкф.

Пример 2. 100 конденсаторов емкостью каждый 2 мкф соединены параллельно. Определить общую емкость. Общая емкость С = 100 Ск = 200 мкф.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Соединения конденсаторов. Энергия электрического поля конденсатора.

Соединения конденсаторов .

Параллельное соединение конденсаторов

Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора

Вывод: При параллельном соединении конденсаторов

• заряды складываются,
• напряжения одинаковые,
• емкости складываются.

Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов

Последовательное соединение конденсаторов

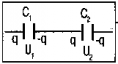
Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С₁ другая от конденсатора С₂ — играют роль обкладок нового конденсатора.

Вывод: При последовательном соединении конденсаторов

• напряжения складываются,
• заряды одинаковы,
• складываются величины, обратные емкости.

Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов.

Энергия электрического поля конденсатора.

Под энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой обкладкой. Тогда:

Формулы справедливы для любого конденсатора.

Пример: С=2мкФ; U=1000В.

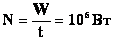
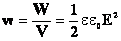
t=10-6c.W=1 Дж — опасно для жизни!

— плотность энергии (энергия единицы объема).

Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических).

Источник

Параллельное и последовательное соединение конденсаторов

Элементы цепи могут быть подключены двумя способами:

Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).

• последовательное соединение конденсаторов

Рис. 1. Последовательное соединение конденсаторов

Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).

Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

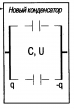
Рис. 2. Последовательное соединение конденсаторов

Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — (помним, что они одинаковы), электроёмкости — , и соответствующие напряжения — и .

• где
  • — напряжение на первом конденсаторе,
  • — электроёмкость первого конденсатора,
  • — заряд конденсатора.

• где
  • — напряжение на втором конденсаторе,
  • — электроёмкость второго конденсатора,
  • — заряд конденсатора.

• где
  • — напряжение полной цепи,
  • — электроёмкость общего конденсатора,
  • — заряд общего конденсатора.

Памятуя о том, что конденсаторы соединены последовательно, получаем:

Или в общем виде:

• где
  • — электроёмкость последовательно соединённых конденсаторов,
  • — сумма обратных емкостей.

Для цепи из двух последовательных соединений:

• параллельное соединение конденсаторов

Рис. 3. Параллельное соединение конденсаторов

Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости

Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:

• где
  • — заряд на первом конденсаторе,
  • — электроёмкость первого конденсатора,
  • — напряжение на первом конденсаторе.

• где
  • — заряд на втором конденсаторе,
  • — электроёмкость второго конденсатора,
  • — напряжение на втором конденсаторе.

• где
  • — заряд на общем конденсаторе,
  • — электроёмкость полного конденсатора,
  • — напряжение на общем конденсаторе.

С учётом того, что , получим:

Или в общем виде:

• где
  • — электроёмкость параллельно соединённых конденсаторов,
  • — сумма электроёмкостей последовательно соединённой цепи.

Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:

• для последовательного соединения
  • заряды всех конденсаторов одинаковы: .
  • напряжение во всей цепи есть сумма напряжений на каждом из элементов: ,
  • полная электроёмкость цепи конденсаторов, соединённых последовательно равна: .
• для параллельного соединения
  • заряд системы конденсаторов есть сумма зарядов на каждом из них: ,
  • напряжение на каждом из элементов одинаково: ,
  • полная электроёмкость цепи конденсаторов, соединённых параллельно равна: .

Поделиться ссылкой:

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

Схемы соединения конденсаторов — расчет емкости

В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.

Последовательное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.

Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:

где: Q₁, Q₂, Q₃ — соответственно заряд на первом, втором, третьем и т.д. конденсаторах

Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:

• U ₁, U₂, U₃ — соответственно напряжение на первом, втором, третьем конденсаторах
• C ₁, C₂, C₃ — соответственно емкости первого, второго, третьего конденсаторов

При этом общее напряжение составит:

Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:

• При последовательном соединении двух конденсаторов:

• При последовательном соединении трех и более конденсаторов:

Параллельное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.

Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:

Заряд же на каждом из конденсаторов будет зависеть от его емкости:

При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:

Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:

Смешанное соединение конденсаторов

Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.

Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.

Для наглядности приведем пример расчета общей емкости данной схемы.

Пример расчета

Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.

Произведем расчет каждой группы:

• Группа 1 — последовательное соединение трех конденсаторов:

• Группа 2 — последовательное соединение двух конденсаторов:

С_4,5 = C ₄* C ₅/ C ₄+ C ₅ = 20*30/20+30 = 600/50 = 12 мкФ

• Группа 3 — параллельное соединение трех конденсаторов:

В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:

• Группа 4 — параллельное соединение двух групп конденсаторов:

С_1,2,3,4,5 = C _1,2,3+ C_4,5 = 2,72+12 = 14,72 мкФ

В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:

С_общ = C _1,2,3,4,5* C _6,7,8/ C _1,2,3,4,5+ C _6,7,8 = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ

Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!

Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.

Источник