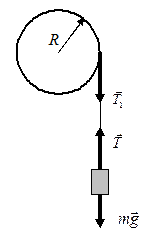Вывод рабочей формулы для экспериментального
определения момента инерции.
При экспериментальном определении момента инерции используется маятник Обербека, который представляет собой крестовину с четырьмя закрепленными на ней на одинаковых расстояниях от оси одинаковыми грузами. На ось крестовины насажен двухступенчатый шкив, на который намотана нить с подвешенным к ней грузом. При движении груза вниз шкив начинает вращаться. Для вывода рабочей формулы рассмотрим упрощенную схему установки, выделив систему связанных движущихся тел: поступательно движущийся груз и вращающийся шкив (рис. 4.1). Поступательное движение груза описывается уравнением:
Вращательный момент шкива создает сила натяжения нити Т1, которая по третьему закону Ньютона равна силе Т. Этот момент М = ТR. Тогда уравнение вращательного движения шкива:
Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза:
Решая систему уравнений (4.1), (4.2) и (4.3), получим для момента инерции выражение: 
.
Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения: h=at 2 /2.
Таким образом, получена рабочая формула для экспериментального определения момента инерции:
(4.4)
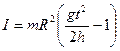
Вывод формулы для теоретического вычисления
Момента инерции.
Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему. Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m2lc 2 /3, где m2 − масса стержня без груза, lc − длина стержня крестовины − указаны на установке. Грузы, укрепленные на крестовине, приближенно можно считать за точечные массы. Тогда момент инерции каждого груза равен m1l 2 , где m1 − масса одного груза (указана на установке), l − расстояние от оси вращения до центра масс груза (измеряется при выполнении работы).
Теоретический момент инерции после суммирования вычисляется по формуле:
Описание экспериментальной установки
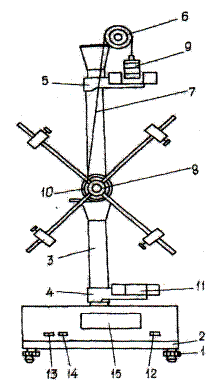
Внешний вид установки представлен на рис.4.2. Регулировочные винты 1 обеспечивают горизонтальную установку основания 2, к которому крепится вертикальная колонка 3, на которой нанесена миллиметровая шкала. К этой колонке прикреплены неподвижный кронштейн 4 и верхний подвижный 5, с помощью которого можно регулировать длину пути груза h. Через диск 6 перекинута нить 7, один конец которой прикреплен к шкиву 8, а на втором конце закреплены грузы 9. Кронштейн 11 снабжен резиновым амортизатором для ограничения движения грузов. Включение прибора производится нажатием клавиши «сеть» 12, обнуление миллисекундомера производится клавишей «сброс» 13, клавиша «пуск» 14 включает миллисекундомер. Время падения груза высвечивается на индикаторе 15.
Порядок выполнения работы
1. Включить установку в сеть.
2. Убедиться, что к нити прикреплен только один груз.
3. Намотать нить на шкив 8, а второй конец с грузом перекинуть через диск 6. Груз поднять на высоту h. Нижний край груза должен совпадать с чертой на корпусе верхнего фотодатчика.
4. Нажать кнопку «пуск» и отпустить груз без толчка. При этом запускается миллисекундомер. Записать отсчет в таблицу 4.1.
5. Нажать кнопку «сброс» и проверить, произошло ли обнуление измерителя.
6. Повторить измерение пять раз, занося значения времени падения в таблицу 4.1.
7. Последовательно увеличивая массу падающего груза, повторить п.п. 3-6.
| № измерения | Груз 1 m (г) = | Грузы 1,2 m (г) = | Грузы 1,2, 3 m (г) = | Грузы 1,2,3,4 m (г) = |
| t1 | ||||
| t2 | ||||
| t3 | ||||
| t4 | ||||
| t5 | ||||
| tср | ||||
| I |
8. Измерить высоту падения груза и длину стержня крестовины. Занести измеренные значения в таблицу 4.2. В эту же таблицу занести значения величин, указанные на установке.
| R |
| m1 |
| m2 |
| I0 |
| lc |
| l |
| h |
9. Вычислить среднее значение времени падения для каждой массы груза и занести в таблицу 4.1.
10. По формуле (4.4) рассчитать значение момента инерции при каждой массе падающего груза, используя среднее время падения, и занести в таблицу 4.1. Ускорение свободного падения для Санкт-Петербурга g = (9,82 ± 0,01) м/с 2 .
11. Рассчитать среднее значение момента инерции и оценить абсолютную и относительную погрешность его определения.
12. По формуле (4.5) вычислить теоретическое значение момента инерции маятника. Сравнить с экспериментально полученным.
13. По формуле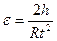 
вычислить угловое ускорение для каждого груза. Вычисленные значения занести в таблицу 4.3.
14. По формуле 
вычислить значение вращающего момента для каждой массы груза. Вычисленные значения занести в таблицу 4.3.
| № груза | m, кг | ε , рад/с | М, Н·с |
15. По данным таблицы 4.3 построить график зависимости углового ускорения от вращающего момента: ε = ε(М).
16. Сделать вывод, подтверждает ли характер зависимости углового ускорения от вращающего момента основной закон динамики вращательного движения. Определить возможные причины отклонения от теоретической зависимости.
17. Определить по графику среднее значение момента инерции маятника как котангенс угла наклона прямой к оси абсцисс.
18. Записать окончательные результаты работы: экспериментально полученное значение момента инерции с погрешностью, теоретическое значение момента инерции и величину момента инерции, вычисленную по графику зависимости ε = ε(М).
Контрольные вопросы
1. Дать определение момента силы относительно точки и относительно оси.
2. Дать определение момента импульса материальной точки относительно точки и относительно оси.
3. Чему равен момент импульса твердого тела относительно оси?
4. Каков физический смысл момента инерции? Как вычислить момент инерции твердого тела?
5. Провести аналогию между характеристиками поступательного и вращательного движения.
6. Указать на чертеже направление момента силы натяжения нити, действующей на шкив в данной работе.
Литература: [1, § 27, 31, 32]; [2, § 30, 33, 36]; [4, §4.1-4.3]; [5].
Источник
Лабораторная работа: Определение момента инерции твердых тел 3
| Название: Определение момента инерции твердых тел 3 Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 17:31:02 06 июня 2011 Похожие работы Просмотров: 288 Комментариев: 15 Оценило: 4 человек Средний балл: 4.3 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||
 |
Для экспериментальной проверки теоремы Штейнера и определения момента инерции в данной работе используется стандартная установка универсального маятника ФПМО — 4. Это настольный прибор (рис. 4.1), на вертикальной стойке основания 1 которого крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360° и фиксация в любом выбранном положении. С одной стороны кронштейна 2 подвешен математический маятник, а с другой — физический. Математический маятник представляет собой металлический шарик 3 на бифилярном подвесе 4. Физический маятник — стальной стержень 5, подвешенный на опорной призме 6. Опорная призма 6 может перемещаться по всей длине стержня и фиксироваться в требуемом положении.
Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на миллисекундомер 9. Миллисекундомер физический выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средняя величина периода колебаний маятника:
где t — продолжительность 10 — 15 колебаний;
n — число колебаний за время t .
Формула для экспериментального расчета момента инерции прямого тонкого стержня
, (3.2)
где T — период колебаний маятника;
l — расстояние от центра масс до точки подвеса маятника;
m — масса маятника;
g — ускорение свободного падения.
Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину:
Формула для теоретического расчета инерции прямого тонкого стержня длиной d и массой mотносительно произвольной оси, параллельной другой оси, перпендикулярной к стержню и проходящей через его середину:
Формула для расчета погрешности косвенного измерения квадрата расстояния между осями:
где s ( l ) – абсолютная погрешность измерения между осями.
Формула для расчета экспериментальной абсолютной погрешности косвенного измерения периода колебания стержня:
(3.6)
Формула для расчета экспериментальной абсолютной погрешности косвенного измерения момента инерции:
(3.7)
где σ ( m ) – абсолютная погрешность измерения массы стержня;
σ ( g ) – абсолютная погрешность измерения ускорения свободного падения;
σ ( π ) – абсолютная погрешность измерения числа π.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты прямых и косвенных измерений представлены в таблице.
| Номер опыта | n | t , c | T , c | l 2 , м 2 | I, кг×м 2 | Примечание |
| 1 | 10 | 12,777 | 1,2777 | 0,0841 | 0,04313 | |
| 2 | 10 | 12,410 | 1,2410 | 0,0625 | 0,03489 | |
| 3 | 10 | 12,156 | 1,2156 | 0,0441 | 0,02837 | |
| 4 | 10 | 12,094 | 1,2094 | 0,0289 | 0,02259 | |
| 5 | 10 | 12,404 | 1,2404 | 0,0169 | 0,01814 | |
| 6 | 10 | 13,471 | 1,3471 | 0,0081 | 0,01489 | |
| 7 | 10 | 16,719 | 1,6719 | 0,0025 | 0,01265 |
Подсчитаем среднюю величину периода колебаний маятника (3.1)
T1 =12,777 / 10 = 1, 2777 с
T2 =12,410/ 10 = 1, 2410 с
T3 =12,156 / 10 = 1, 2156 с
T4 =12,094 / 10 = 1, 2094 с
T5 =12,404 / 10 = 1,2404 с
T6 =13,471 / 10 = 1,3471 с
T7 =16,719 / 10 = 1,6719 с
Теперь найдем момент инерции прямого тонкого стержня по формуле (3.2)
I1 = 
≈ 0,04313 кг*м 2
I2 = 
≈ 0,03489кг*м 2
I3 = 
≈ 0,02837 кг*м 2
I4 = 
≈ 0,02259кг*м 2
I5 = 
≈ 0,01814кг*м 2
I6 = 
≈ 0,01489кг*м 2
I7 = 
≈ 0,01265 кг*м 2
Абсолютная погрешность замера времени колебаний составляет ± 2 мс, а с учётом вычисления периода ± 2×10 -4 , то вычисляем результаты с точностью до пяти знаков.
Расчёт случайной погрешности измерения для построения графика
t1 = 
σ (t) = 12,777 0,02с
t2 = σ (t) = 12,410 0,02с
t3 = σ (t) = 12,156 0,02с
t4 = σ (t) = 12,094 0,02с
t5 = σ (t) = 12,404 0,02с
t6 = σ (t) = 13,471 0,02с
t7 = σ (t) = 16,719 0,02с
От абсолютной погрешности замера времени колебаний зависит момент инерции прямого тонкого стержня, а расстояние от масс до точки подвеса маятника не зависит.
T1 = σ (t) / n = 1,27770,002с
T2 = σ (t) / n = 1,24100,002с
T3 = σ (t) / n = 1,21560,002с
T4 = σ (t) / n = 1,20940,002с
T5 = σ (t) / n = 1,24040,002с
T6 = σ (t) / n = 1,34710,002с
T7 = σ (t) / n = 1,67190,002с
I1 max = 0,04315 кг*м 2 I1 min = 0,04311кг*м 2
I2 max = 0,03491 кг*м 2 I2 min = 0,03487кг*м 2
I3 max = 0,02839 кг*м 2 I3 min = 0,02835кг*м 2
I4 max = 0,02261кг*м 2 I4 min = 0,02257кг*м 2
I5 max = 0,01816кг*м 2 I5 min = 0,01812кг*м 2
I6 max = 0,01491кг*м 2 I6 min = 0,01487кг*м 2
I7 max = 0,01267кг*м 2 I7 min = 0,01263кг*м 2
Теоретический расчет момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину находим по формуле (3.5).
s ( I 0 )=(0.62 2 /12)*0.007= 0.0002 кг*м 2
Расчет погрешности косвенного измерения l 2 производим по формуле (3.5). Величину погрешности измерения l принимаем равной половине величины наименьшего деления шкалы расстояний или s ( l ) = 0,005.
Находим погрешности l 2 для каждого измерения:
1. s (l 2 )= 2*0,29*0,005=0,0029 м 2
2. s (l 2 )= 2*0,25*0,005=0,025 м 2
3. s (l 2 )= 2*0,21*0,005=0,0021 м 2
4. s (l 2 )= 2*0,17*0,005=0,0017 м 2
5. s (l 2 )= 2*0,13*0,005=0,0013 м 2
6. s (l 2 )= 2*0,09*0,005=0,0009 м 2
7. s (l 2 )= 2*0,05*0,005=0,0005 м 2
Экспериментальный расчет погрешностей косвенного измерения I произ-
водится по формуле (3.7), где s ( g )=0,01 и s (П)=0,01 (из справочников). s ( T )=1/10*0,002= 0,0002 (найдено по формуле (3.6). s ( l) = 0,005 половина деления прибора.
1. s ( I) = 0,0059≈0,006 кг*м 2
2. s ( I)= 0.0012≈0,001 кг*м 2
3. s (I)= 0.00082≈0,001 кг*м 2
4. s (I)= 0.00067≈0,001 кг*м 2
5. s (I)= 0.00064≈0,001 кг*м 2
6. s (I)= 0.00064≈0,001 кг*м 2
7. s (I)= 0.00067≈0,001 кг*м 2
Теоретический расчет момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину находим по формуле (3.3):
I0 =(0,358*0,62 2 )/12=0,0114 кг*м 2
Используя график на (рис.1) определим собственный момент инерции I0 и массу стержня m:
b-это отрезок, который прямая линия графика отсекает от оси ординат (на вертикальной оси). Нужно определить ординату их точки пересечения. Но это правило справедливо в том случае, когда координатные оси пересекаются в начале координат, т.е. в точке с координатами (0;0). В нашем случае надо использовать другое правило: надо выбрать две точки на прямой, например точки с координатами 
и 
и записать уравнение прямой, проходящей через эти точки:
Приведение этого уравнения к виду y=ax+b дает следующие выражение для b:
Следовательно: b=
Где: 
Найденные из графика: собственный момент инерции I0 и масса стержня m совпадают в пределах погрешности с теоретическими.
В результате проделанной работы мы убедились в справедливости теоремы Штейнера I = I0 +ml 2 , так как смогли в пределах погрешностей измерений построить линеаризованный график зависимости I= f (l 2 ).
6. Контрольные вопросы.
6.1. Как формируются понятия инерции материальной точки и твердого тела?
Моментом инерции материальной точки относительно неподвижной оси вращения называется физическая величина I, равная произведению массы m материальной точки на квадрат расстояния r ² до оси:
Момент инерции твёрдого тела относительно неподвижной оси вращения, складывается из моментов инерции отдельных его материальных точек:
6.2. В каких ситуациях применима теорема Штейнера?
Если известен момент инерции тела относительно любой оси проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.
6.3. Как формируется теорема Штейнера?
Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
6.4. Под действием какой силы совершается колебательное движение маятника?
Под действием составляющей силы тяжести P1 = Psinφ .
6.5. Является ли момент инерции аддитивной величиной?
Является. Так как к аддитивным величинам относятся масса, энергия, импульс, момент импульса, объем, момент энергии.
6.6. Объяснить метод определения момента инерции с помощью физического маятника.
По основному закону динамики вращательного движения:
M = I∙β = — m∙g∙l∙φ (для малых углов отклонения); так как β = d 2 φ/dt 2 , то получаем дифференциальное уравнение гармонических колебаний:
, где 
; период колебаний
; отсюда получаем выражение 
Зная ускорение свободного падения g , массу m , экспериментально измерив l и определив Т , тогда можно вычислить момент инерции маятника .
6.7. Какой маятник называется физическим?
Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной оси, не проходящей через центр масс.
6.8. При каких формальных допущениях справедлива формула (3,7)?
Период колебаний маятника равен:
. Эта формула справедлива когда моментом силы трения можно пренебречь а также силой сопротивления воздуха, так маятник отклоняется на малые углы φ, то допускается sinφ ≈ φ.
6.9. Как записывается основной закон динамики вращательного движения?
Основной закон динамики вращательного движения записывается так: 
, что является аналитической формой основного уравнения (закона) динамики вращательного движения : при воздействии момента внешних сил твердое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорционально моменту сил и обратно пропорционально моменту инерции тела относительно данной оси.
Источник
