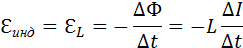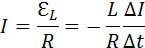Выведите формулу выражающую энергию магнитного поля
Рассмотрим случай, о котором мы уже говорили (рис. 5.6).
Сначала замкнем соленоид L на источник ЭДС 
, в нем будет протекать ток 
. Затем в момент времени 
переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа: 
, или
 , | (5.5.1) |
Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией
 , | (5.5.3) |
Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:
.
; отсюда 
Подставим эти значения в формулу (5.5.3):
 , | (5.5.4) |
Обозначим w – плотность энергии, или энергия в объеме V, тогда
 , | (5.5.5) |
но т.к. 
, то
 или  | (5.5.6) |
Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле
 , | (5.5.7) |
а плотность энергии
 , | (5.5.8) |
Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:
, отсюда 
.
Т.к. в вакууме 
, имеем
1. Какие опыты Фарадея легли в основу открытия явления электромагнитной индукции?
2. Что является причиной возникновения ЭДС индукции в замкнутом проводящем контуре? От чего и как зависит ЭДС индукции, возникающая в контуре?
3. В чем заключается явление электромагнитной индукции?
4. Почему для обнаружения индукционного тока лучше использовать замкнутый проводник в виде катушки, а не в виде одного витка провода?
5. Сформулируйте правило Ленца, проиллюстрировав его примерами.
6. Как направлен индукционный ток?
7. Всегда ли при изменении магнитной индукции в проводящем контуре в нем возникает ЭДС индукции? индукционный ток?
8. Чему равна ЭДС индукции контура?
9. Сформулируйте закон Ома для контура.
10. Как связано направление индукционного тока и направление скорости изменения потока магнитной индукции?
11. Сформулируйте закон Фарадея для контура с током, состоящего из одного и нескольких витков.
12. Возникает ли индукционный ток в проводящей рамке, поступательно движущейся в однородном магнитном поле?
13. Покажите, что закон Фарадея есть следствие закона сохранения энергии.
14. Какова природа ЭДС электромагнитной индукции?
15. Выведите выражение для ЭДС индукции в плоской рамке, равномерно вращающейся в однородном магнитном поле. За счет чего ее можно увеличить?
16. Что такое вихревые токи? Вредны они или полезны?
17. Почему сердечники трансформаторов не делают сплошными?
18. Какое явление называется скин-эффектом?
19. Произведите классификацию ускорителей.
20. Каковы параметры линейных ускорителей.
21. Когда заряженная частица движется в магнитном поле по спирали? От чего зависит шаг спирали? Ответы подтвердите выводами формул.
22. Что такое ускорители заряженных частиц? Какие они бывают и чем характеризуются?
23. Почему для ускорения электронов не применяются циклотроны?
24. В чем заключается принцип автофазировки? Где он используется?
25. Когда ЭДС самоиндукции больше – при замыкании или размыкании цепи постоянного тока?
26. В чем заключается физический смысл индуктивности контура? взаимной индуктивности двух контуров? От чего они зависят?
27. В чем заключаются явления самоиндукции и взаимной индукции? Вычислите ЭДС индукции для обоих случаев.
28. В чем заключается физический смысл времени релаксации 
? Докажите, что 
имеет размерность времени.
29. Запишите и проанализируйте выражения для объемной плотности энергии электростатического и магнитного полей. Чему равна объемная плотность энергии электромагнитного поля?
30. Напряженность магнитного поля возросла в два раза. Как изменилась объемная плотность энергии магнитного поля?
31. Приведите соотношение между точками в первичной и вторичной обмотках повышающего трансформатора.
В таблице 5.1 приведены сравнительные характеристики электрического и магнитного полей.
Источник
Самоиндукция. Энергия магнитного поля
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
1 Гн = 1 Вб / 1 А.
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой:
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.
Магнитный поток, пронизывающий все N витков соленоида, равен
Следовательно, индуктивность соленоида равна
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз; поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
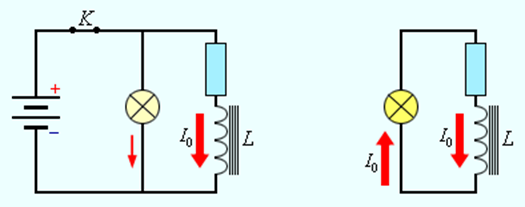
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает
Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I 2 R Δt.
Ток в цепи равен
Выражение для ΔQ можно записать в виде
В этом выражении ΔI Опубликовано в разделах: Электродинамика, Магнитное поле
Источник
Магнитная энергия контура с током
Электрический ток обладает запасом так называемой магнитной энергии. Если в процессе вычисления данной энергии принимать все провода за идеально проводящие, то это не повлияет на результат, по той причине, что магнитная энергия зависима лишь от величины и распределения токов, а также от магнитных свойств заполняющей пространство среды.
Вывод формулы энергии магнитного поля
Для начала рассмотрим случай с одиночным неподвижным замкнутым контуром (витком проводника).
Пускай изначально сила тока в нем равняется нулю. Не важно каким способом доводим значение тока в витке до I . Вместе с ростом тока в контуре повышается и значение магнитного потока Ф , проходящего через него. Возникает электродвижущая сила (ЭДС) индукции. Элементарная работа, производимая внешним источником против ЭДС индукции, будет эквивалентна следующему выражению: δ A в н е ш = — ε и н д I d t .
Применяя закон Фарадея, выводим: δ A в н е ш = 1 c I d Φ .
Данное соотношение носит общий характер. Оно является справедливым и для ферромагнитных материалов, ведь в процессе его вывода относительно магнитных свойств среды не вводилось никаких предположений. Однако стоит отметить, что в случае, когда среда не обладает гистерезисом, к примеру, являясь пара- или диамагнетиком, δ A в н е ш будет применяться исключительно в целях роста значения магнитной энергии W m , соответственно:
Исходя из условий закона Био-Савара-Лапласа, можно заявить, что индукция магнитного поля тока линейно зависима от силы тока. В условиях переменной силы тока, протекающего по жесткому неподвижному контуру, картина силовых линий не претерпевает изменений, а индукция в каждой точке прогрессирует пропорционально силе тока. Соответственно, поток магнитной индукции Ф , проходящий через неизменную и недвижимую площадь, тоже пропорционален силе тока, по этой причине: Φ = L I c ,
где L представляет собой индуктивность контура, постоянный коэффициент пропорциональности, не обладающий зависимостью от силы тока и индукции магнитного поля. Подставим ( 5 ) в ( 4 ) , получим:
Из формулы ( 6 ) следует, что:
Формула W m = L 2 I c 2 = 1 2 c определяет энергию магнитного поля, формирующегося током ( I ) , который протекает по контуру с индуктивностью L .
Формула W m = L 2 I c 2 = 1 2 c может быть записана в следующем виде: W m = 1 c ∫ ∑ I i ‘ d Φ i ‘ .
Для справедливости формул W m = L 2 I c 2 = 1 2 c и I Φ = Φ 2 2 L незначительно, что виток в процессе возрастания тока остается неподвижным, по той причине, что энергия зависима лишь от состояния системы, а не от способа достижения такого состояния.
Примеры решения задач
Задание: Сила тока в витке эквивалентна I = 1 А . Магнитный поток Ф , проходящий через площадь витка составляет 100 м к В б . Найдите энергию магнитного поля в витке.
Решение
В качестве фундамента решения задачи примем формулу: W m = 1 2 I Φ .
Переведем величину магнитного потока, заданного в условиях задачи, в систему С И : 100 м к В б = 10 — 4 В б .
Проведем вычисления: W m = 1 2 · 1 · 10 — 4 = 5 · 10 — 3 ( Д ж ) .
Ответ: W m = 5 · 10 — 3 ( Д ж ) .
Задание: Рядом друг с другом расположены два витка проводника. По первому протекает ток I = 1 А . Второй соединен с баллистическим гальванометром, при выключении тока в контуре ( 1 ) через гальванометр проходит заряд q = 10 — 8 К л . Полное сопротивление цепи равно R = 5 О м . Чему равняется взаимная индуктивность витков?
Решение
Магнитная энергия ( W m ) витка с током может быть записана как: W m = L I 2 2 . С другой стороны энергия витка, который соединен с гальванометром, может быть рассчитана как: W m ‘ = q U 2 . Заряд на втором контуре появляется благодаря тому, что он находится в переменном магнитном поле первого витка, и по закону сохранения энергии мы можем записать, что: W m ‘ = W m . Следовательно, мы можем приравнять и правые части выражений W m = L I 2 2 и W m ‘ = q U 2 , получим: L I 2 2 = q U 2 → L I 2 = q U . Из уравнения выше выразим индуктивность: L = q U I 2 . По закону Ома для участка цепи имеем: U = I R . Соответственно: L = q R I .
Эта задача может быть решена иным способом. Обозначим через ε 2 ЭДС индукции, которая вызвана переменным магнитным полем, которое создается в момент выключения тока в первом контуре: ε 2 = — L d I d t . ЭДС индукции можно записать по закону Ома следующим образом: ε 2 = I 2 R , где силу тока найдем как: I 2 = d q d t , в таком случае выражение ε 2 = I 2 R преобразуется в формулу вида: ε 2 = d q d t R . Приравняем правые части выражений ε 2 = — L d I d t и ε 2 = d q d t R , на выходе получим: — L d I d t = d q d t R → — L d I = R d q .
Проинтегрируем приведенную выше формулу с учетом того, что ток в первом контуре меняется от I до нуля, а заряд во втором от нуля до q , получим: — L ∫ I 0 d I = R ∫ 0 q d q → L I = R q → L = R q I .
Данный метод дает абсолютно такой же результат. Таким образом, раз все величины в условиях задачи приведены в системе С И , произведем вычисления: L = 10 — 8 · 5 1 = 5 · 10 — 8 ( Г н ) .
Источник
