Выведите формулы момент инерции диска

Момент инерции для чайников: определение, формулы, примеры решения задач

• 12 января 2021 г.
• 7 минут
• 329 935

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Источник

Момент инерции диска. Явление инерции

Многие люди замечали: когда они едут в автобусе, и он увеличивает свою скорость, их тела прижимаются к креслу. И наоборот, при остановке транспортного средства пассажиров будто выбрасывает из посадочных мест. Все это происходит из-за инерции. Рассмотрим это явление, а также объясним, что такое момент инерции диска.

Что представляет собой инерция?

Под инерцией в физике понимают способность всех тел, обладающий массой, сохранять покоящееся состояние либо двигаться с одинаковой скоростью в одном и том же направлении. Если необходимо изменить механическое состояние тела, то приходится прикладывать некоторую внешнюю силу к нему.

Вам будет интересно: Особенности и отличия австралийского английского языка от британского

В данном определении следует обратить внимание на два момента:

• Во-первых, это вопрос состояния покоя. В общем случае такого состояния не существует в природе. Все в ней находится в постоянном движении. Тем не менее, когда мы едем в автобусе, то нам кажется, что водитель не двигается со своего места. В таком случае идет речь об относительности движения, то есть относительно пассажиров водитель находится в покое. Отличие между состояниями покоя и равномерного движения заключается лишь в системе отсчета. В примере выше пассажир в состоянии покоя относительно автобуса, в котором едет, но движется относительно остановки, которую проезжает.
• Во-вторых, инерция тела пропорциональна его массе. Наблюдаемые нами объекты в жизни все имеют ту или иную массу, поэтому все они характеризуются некоторой инертностью.

Таким образом, инерция характеризует степень трудности изменения состояния движения (покоя) тела.

Инерция. Галилей и Ньютон

Когда изучают вопрос инерции в физике, то как правило, связывают ее с первым ньютоновским законом. Этот закон гласит:

Любое тело, на которое не действуют внешние силы, сохраняет свое состояние покоя либо равномерного и прямолинейного движения.

Считается, что этот закон сформулировал Исаак Ньютон, и произошло это в середине XVII века. Отмеченный закон справедлив всегда и во всех процессах, описываемых классической механикой. Но когда ему приписывают фамилию английского ученого, следует сделать некоторую оговорку.

В 1632 году, то есть за несколько десятков лет до постулирования закона инерции Ньютоном, итальянский ученый Галилео Галилей в одной из своих работ, в которой он сравнивал системы мира Птолемея и Коперника, по сути сформулировал 1-й закон «Ньютона»!

Галилей говорит, что если тело движется по гладкой горизонтальной поверхности, и силами трения и сопротивления воздуха можно пренебречь, то это движение будет сохраняться вечно.

Вращательное движение

Приведенные выше примеры рассматривают явление инерции с точки зрения прямолинейного перемещения тела в пространстве. Однако существует еще один тип движения, который распространен в природе и Вселенной — это вращение вокруг точки или оси.

Масса тела характеризует его инерционные свойства поступательного движения. Для описания же аналогичного свойства, которое проявляет себя при вращении, вводят понятие момента инерции. Но перед тем как рассматривать эту характеристику, следует познакомиться с самим вращением.

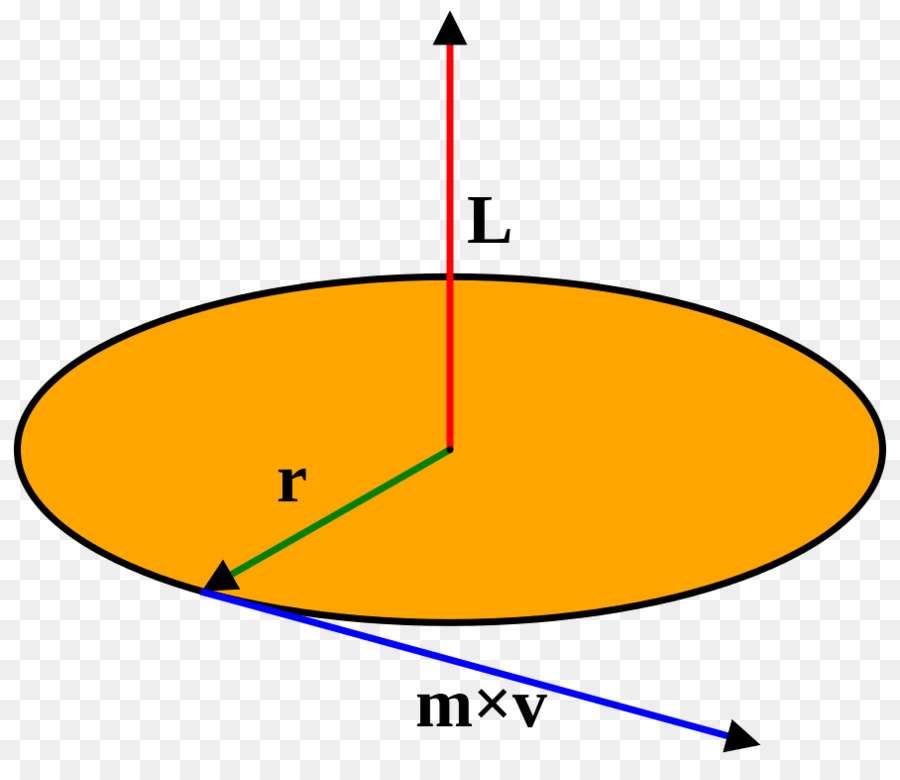
Круговое перемещение тела вокруг оси или точки описывается двумя важными формулами. Ниже они приводятся:

В первой формуле L — это момент импульса, I — момент инерции, ω — угловая скорость. Во втором выражении α — это ускорение угловое, которое равно производной по времени от угловой скорости ω, M — момент силы системы. Он рассчитывается как произведение результирующей внешней силы на плечо, к которому она приложена.

Первая формула описывает вращательное движение, вторая — его изменение во времени. Как видно, в обеих этих формулах присутствует момент инерции I.

Момент инерции

Сначала приведем его математическую формулировку, а затем объясним физический смысл.

Итак, момент инерции I рассчитывается следующим образом:

Если перевести это выражение с математического на русский язык, то оно означает следующее: все тело, которое имеет некоторую ось вращения O, разбивается на мелкие «объемчики» массой mi, находящиеся на расстоянии ri от оси O. Момент инерции рассчитывается путем возведения в квадрат этого расстояния, его умножения на соответствующую массу mi и сложения всех полученных слагаемых.

Если разбить все тело на бесконечно малые «объемчики», тогда сумма выше будет стремиться к следующему интегралу по объему тела:

I = ∫V(ρ *r2dV), где ρ — плотность вещества тела.

Из приведенного математического определения следует, что момент инерции I зависит от трех важных параметров:

• от значения массы тела;
• от распределения массы в теле;
• от положения оси вращения.

Физический смысл момента инерции заключается в том, что он характеризует, насколько «тяжело» привести в движение вращения данную систему или изменить ее скорость вращения.

Момент инерции диска однородного

Полученные в предыдущем пункте знания применимы для расчета момента инерции однородного цилиндра, который в случае h Понравилась статья? Поделись с друзьями:

Источник

7.1. Динамика вращения вокруг неподвижной оси

Движение материальной точки характеризуется перемещением, скоростью, ускорением. Но при вращении твердого тела все его элементы имеют разные перемещения, различные скорости. Удобно найти переменные, одинаковые для всех элементов твердого тела. Мы их, собственно, уже знаем — угол поворота, угловая скорость, угловое ускорение. Соответственно, изучая динамику вращения, вместо импульса и силы мы будем оперировать их угловыми аналогами — моментом импульса и моментом силы.

Уравнение движения. В теме 4.8 было выведено уравнение движения системы материальных точек в виде

где моменты импульса и силы определялись как

Внутренние силы между телами системы, напомним, выпали из уравнений движения. Абсолютно твердое тело можно рассматривать как систему частиц (материальных точек) с неизменными расстояниями между ними. Поэтому выписанные уравнения применимы для твердого тела, а неизменность расстояний между его точками позволяет характеризовать вращение тела вокруг неподвижной оси единственной координатой — углом поворота. Поэтому мы можем упростить приведенное выше уравнение движения. Прежде всего, нас не интересуют в данный момент напряжения, возникающие в оси. Кроме того, для описания вращения достаточно рассмотреть проекции векторов моментов импульса и силы на ось вращения.

Рис. 7.1. Момент импульса L двух шаров массы m, соединенных стержнем. Вся система вращается вокруг оси z c угловой скоростью ω

Направим ось z вдоль оси вращения и выделим в твердом теле элемент массой , положение которого характеризуется радиус-вектором (рис. 7.2).

Рис. 7.2 Вращение твердого тела вокруг неподвижной оси 0z

Момент импульса этого элемента есть

Рис. 7.3. Момент импульса системы направлен вдоль оси вращения.

Радиус-вектор можно представить как сумму его проекций на ось z и плоскость ху :

где вектор лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:

Первое слагаемое — вектор, направленный противоположно Поэтому оно не дает вклада в z-компоненту момента импульса. Второе слагаемое — вектор, направленный вдоль оси z. Так как

Суммируя по всем элементам тела, получаем

Величина называется моментом инерции тела.

Говоря о моменте инерции, всегда указывают, относительно какой именно оси вращения он определен (в данном случае — это ось z). Момент инерции того же тела относительно какой-то другой оси примет иное значение. Сохраняется только общее правило его вычисления: берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения.

В случае непрерывного распределения масс с плотностью сумма заменится на интеграл по всему объему тела:

Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.

Записываем теперь уравнение движения в проекции на ось z :

Если момент инерции не зависит от времени, то дифференцировать нужно только угловую скорость, в результате получаем основное уравнение динамики вращательного движения твердого тела в виде

Производная угловой скорости по времени — это угловое ускорение

Видео 7.1. Основное уравнение динамики вращательного движения. Демонстрация, вытекающей из него связи между угловым ускорением, моментом силы и моментом инерции

Рассмотрим теперь момент внешних сил. Разложим силу на вектор в направлении оси z и вектор, ей ортогональный:

Используя снова аналогичное разложение радиус-вектора

получаем для момента внешних сил :

Первое слагаемое равно нулю. Два следующих содержат единичный орт — вектор k, направленный вдоль оси 0z и, следовательно, не дают вклада в проекцию . Оба вектора

лежат в плоскости xy и, следовательно, последнее слагаемое направлено параллельно оси 0z. Если — угол между этими векторами, то

где — плечо силы (см. тему. 4.8). Силу

надо здесь понимать в алгебраическом смысле: она входит со знаком минус, если сила тормозит вращение.

Момент инерции. Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

Рис. 7.4. Моменты инерции различных тел

1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.

Обруч считается бесконечно тонким, то есть толщиной обода можно пренебречь по сравнению с радиусом . Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, можно вынести из-под знака интеграла:

где — полная масса обруча.

2. Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр.

Диск считается бесконечно тонким, если его толщина много меньше радиуса . Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом и шириной (рис. 7.5).

Рис. 7.5 Вычисление момента инерции диска относительно оси z, перпендикулярной его плоскости и проходящей через центр

Площадь поверхности обруча равна произведению его длины окружности на ширину: . Поскольку масса m диска распределена равномерно, масса единицы площади равна , так что масса обруча равна

Момент инерции обруча мы уже знаем:

Осталось просуммировать моменты инерции всех таких обручей:

Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.

3. Момент инерции шара относительно его диаметра.

Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщиной , находящиеся на расстоянии z от центра (рис. 7.6).

Рис. 7.6. Момент инерции шара относительно его диаметра

Радиус такого диска

Объем диска равен его площади, умноженной на толщину:

Массу диска находим, разделив массу шара на его объем и умножив на объем диска:

Момент инерции диска был найден выше. В применении к данному случаю он равен

Момент инерции шара находится интегрированием по всем таким дискам:

4. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.

Пусть стержень имеет длину . Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).

Рис. 7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню

Возьмем элемент стержня длиной , находящийся на расстоянии x от оси вращения. Его масса равна

а момент инерции

Отсюда находим момент инерции стержня:

Теорема Штейнера. В приведенных примерах оси проходят через центр масс (центр инерции) тела. Момент инерции относительно других осей вращения определяется в соответствии с теоремой Штейнера:

Рис. 7.8. К выводу теоремы Штейнера

Момент инерции тела относительно произвольной оси равен сумме момента инерции J_C относительно параллельной оси, проходящей через центр инерции тела, и величины ma 2 — произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси, то есть

Продемонстрируем сначала применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:

Расстояние до оси, проходящей через центр масс, равно a = l/2. По теореме Штейнера получаем тот же результат:

Вывод теоремы Штейнера иллюстрируется рис. 7.8, 7.9

Рис. 7.9. К выводу теоремы Штейнера

Пусть одна ось проходит в направлении единичного вектора n через центр масс С твердого тела (системы тел), а другая — параллельно ей через некоторую точку 0. Из центра масс в направлении второй оси проводим ортогональный осям вектор a, который определяет положение точки 0. Радиус-векторы некоторого элемента системы массой относительно точек С и 0 обозначаем и , соответственно. Момент инерции этого элемента относительно оси С есть

где — расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).

Катет равен проекции векторов и на ось вращения, то есть

Используя эти выражения и суммируя по всем элементам системы, находим момент инерции относительно оси, проходящей через точку С, и, аналогичным образом, момент инерции относительно параллельной оси, проходящей через точку 0 :

Здесь выражение для получено из простой заменой на .

Как видно из рис. 7.9, векторы и связаны между собой:

так как векторы n и а ортогональны и их скалярное произведение

Тогда мы можем преобразовать выражение для :

Первое слагаемое в правой части — момент инерции относительно оси, проходящей через точку C. Третье слагаемое равно , где

— полная масса системы.

Второе слагаемое равно нулю, так как оно пропорционально радиус-вектору центра инерции относительно самого центра инерции. Окончательно:

что и требовалось доказать.

Теорема Штейнера связывает моменты инерции относительно параллельных осей. Иногда оказывается полезной другая теорема, связывающая моменты инерции относительно трех взаимно перпендикулярных осей. Однако эта теорема относится только к плоским фигурам, толщиной которых можно пренебречь по сравнению с размерами в двух других направлениях. Итак, теорема о моментах инерции плоских фигур:

Если через произвольную точку 0 плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку 0.

Иными словами, берем на фигуре произвольную точку 0 и проводим координатные оси так, чтобы 0x и 0y лежали в плоскости фигуры. Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:

При этом расположение осей 0x, 0y может быть произвольным; главное, чтобы они лежали в плоскости фигуры (рис. 7.10).

Рис. 7.10. Моменты инерции плоской фигуры относительно взаимно перпендикулярных осей

Из рисунка видно, что

что и требовалось доказать.

Найдем, например, момент инерции диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому

Согласно теореме о плоской фигуре

Теперь можно применить теорему Штейнера, чтобы найти, например, момент инерции относительно оси , параллельной диаметру и проходящей через край диска (см. рис. 7.10):

Источник