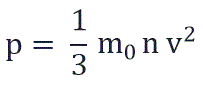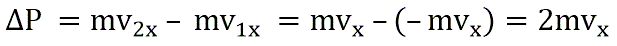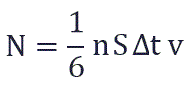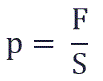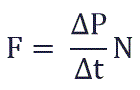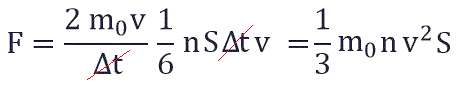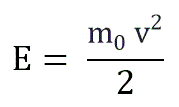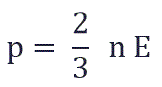Выведите основное уравнение молекулярно кинетической теории

Основное уравнение молекулярно-кинетической теории (МКТ) с выводом

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

• молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
• при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

p – давление молекул газа на границы емкости,

m₀ – масса одной молекулы,

n — концентрация молекул, число частиц N в единице объема V;

v 2 — средне квадратичная скорость молекул.

Вывод основного уравнения МКТ

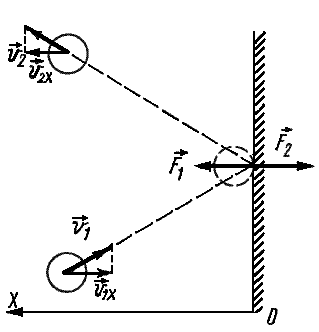
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция v_x скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv_1x = –mv_x на mv_2x = mv_x.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

S – площадь этой стенки

n — концентрация частиц

Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

Если заменить среднее значение кинетической энергии поступательного движения молекул — E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Понравилась статья, расскажите о ней друзьям:

Источник

Выведите основное уравнение молекулярно кинетической теории

162 дн. с момента
до конца учебного года

Основное уравнение МКТ

Слово «газ» в переводе с греческого звучит как «хаос». Это отлично характеризует движение частичек, которое на самом деле беспорядочно и хаотично. Газ не образует определенной поверхности, он заполняет весь доступный ему объем. Такое состояние веществ — самое распространенное в нашей Вселенной.

Законы, которые определяют свойства и поведение такого вещества, легче всего формулировать и рассматривать на примере состояния, в котором относительная плотность молекул и атомов низкая. Оно получило название «идеальный газ». В нем расстояние между частицами больше, чем радиус взаимодействия межмолекулярных сил.

Итак, идеальный газ — это теоретическая модель вещества, в которой почти полностью отсутствует взаимодействие частиц.

Как показывает опыт, молекулы газа распределяются по всему предоставленному для него объему. Следовательно, главную роль в поведении газа играет хаотическое движение молекул, а силы взаимодействия малы, и ими можно пренебречь. Это означает, что молекула газа движется равномерно и прямолинейно, пока не столкнется с другой молекулой. При столкновении изменяется величина и направление скорости движения молекулы, и она снова движется равномерно и прямолинейно до следующего столкновения. Дли на свободного пробега (расстояние между двумя последовательными столкновениями молекулы) λ

10 -7 м. При такой длине свободного пробега только 0,04 % пространства, занятого газом, приходится на собственный объем его молекул. Это дает право воспользоваться моделью идеального газа.

Идеальный газ — это газ с достаточно простыми свойствами:

1. Между частицами идеального газа нет сил взаимодействия; они действуют только при столкновениях частиц (т.е. потенциальная энергия взаимодействия частиц идеального газа настолько мала, что ею пренебрегают по сравнению с кинетической энергией);
2. Частицы в идеальном газе имеют настолько маленькие размеры, что их можно считать материальными точками. Их суммарный объём ничтожно мал по сравнению с объёмом сосуда, в котором находится газ. И этим объёмом пренебрегают;
3. От столкновения до столкновения частицы движутся равномерно и прямолинейно;
4. Движение частиц идеального газа подчиняется законам Ньютона;
5. Частицы идеального газа ведут себя при столкновениях как абсолютно упругие шарики;
6. Среднее время между столкновениями частиц намного превышает время их взаимодействия при соударении. Поэтому временем взаимодействия пренебрегают также.

При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.

Реальные газы при комнатной температуре и нормальном давлении ведут себя как идеальные газы. Идеальными газами можно считать такие газы как гелий, водород, свойства которых уже при обычных условиях отвечают закономерностям идеального газа.

Для описания свойств газов можно пользоваться:

1. микроскопическими параметрами (скорость, масса молекулы, ее энергия и др.), которые являются характеристиками молекул и средние численные значения которых находятся только расчетным путем;
2. макроскопическими параметрами (давление, температура, объем газа), значение которых определяется совместным действием огромного числа молекул. Макропараметры — это параметры, характеризующие состояние системы (газа) в целом и не имеющие смысла в применении к отдельным частицам системы. Численные значения их находят измерением с помощью приборов и расчетным путем.

Давление газа p — это средняя сила ударов его молекул о тело (например, о стенки сосуда), отнесенная к единице поверхности тела.

Абсолютная температура T — мера средней кинетической энергии теплового движения молекулы (см. Температура и тепловое равновесие системы).

Под объемом газа V понимают внутренний объем сосуда, в котором находится газ.

P =1/3 m_onV 2 — основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его частиц о стенки сосуда.

Источник

Физика. 10 класс

Конспект урока

Физика, 10 класс

Урок 18. Основное уравнение МКТ

Перечень вопросов, рассматриваемых на уроке:

1) средняя кинетическая энергия молекулы;

2) давление газа;

3) основное уравнение МКТ;

Глоссарий по теме:

Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.

Средняя кинетическая энергия молекул – усреднённая величина, равная половине произведения массы молекулы на среднюю величину квадрата её скорости.

Концентрация – число молекул в единице объёма.

Масса молекулы (или атома) – чрезвычайно маленькая величина в макроскопических масштабах (граммах и килограммах), вычисляется через отношение массы вещества к количеству содержащихся в ней молекул (или атомов).

Изменение импульса тела – произведение силы на время действия силы. Импульс силы всегда показывает, как изменяется импульс тела за данное время.

Основная и дополнительная литература по теме урока:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 188 – 192.
2. Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. С. 111.
3. Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. С. 65 – 67.

Открытые электронные ресурсы по теме урока:

Теоретический материал для самостоятельного изучения

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами — массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.

Давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы m₀v.

Давление пропорционально второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:

, где m₀ — масса одной молекулы газа,

n— концентрация молекул,

— среднее значение квадрата скорости молекул.

Коэффициент обусловлен трёхмерностью пространства — во время хаотического движения молекул все три направления равноправны.

Средняя кинетическая энергия поступательного движения

тогда уравнение примет вид:

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Примеры и разбор решения заданий.

1. К каждой позиции первого столбца подберите соответствующую позицию второго:

А)

2) средняя кинетическая энергия молекул

Б)

3) давление газа на стенку сосуда

В)

4) концентрация молекул

Г)

Правильный ответ: вспомнив формулы величин, устанавливаем соответствие:

В)

2) средняя кинетическая энергия молекул

А)

3) давление газа на стенку сосуда

Г)

4) концентрация молекул

Б)

2. Кислород находится при нормальных условиях. Средняя квадратичная скорость молекул кислорода в этом случае равна ___ м/с.

Источник