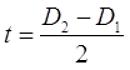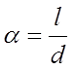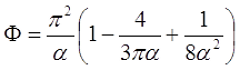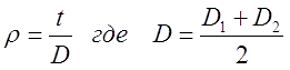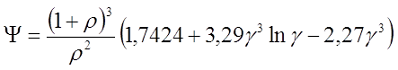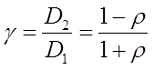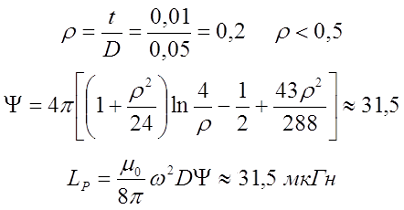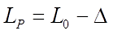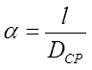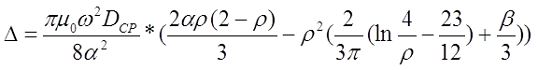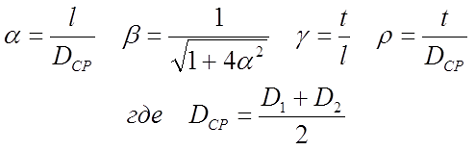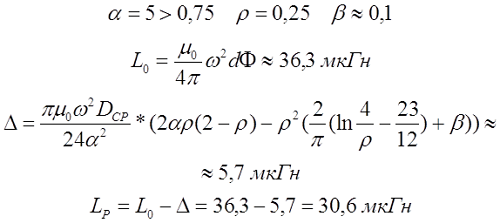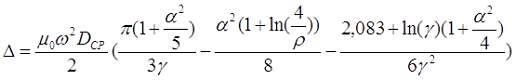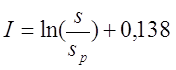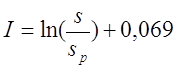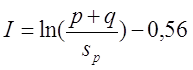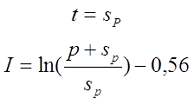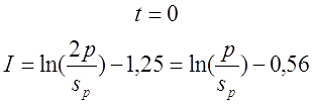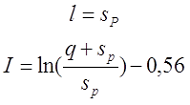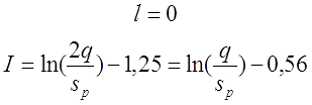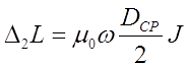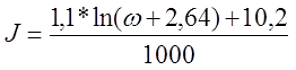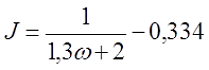Выведите рабочую формулу для определения индуктивности соленоида

Лабораторная работа № 49

Цель работы — определение индуктивности соленоида по его сопротивлению переменному току.

Приборы и принадлежности: исследуемый соленоид, звуковой генератор, электронный осциллограф, миллиамперметр переменного тока, соединительные провода.

Явление самоиндукции. Индуктивность

Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий проводящий контур. В частности, если электрический ток течет в проводящем контуре, то он создает пронизывающий этот контур магнитный поток Ф.

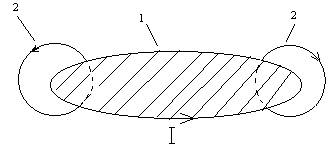
При изменении силы тока I в любом контуре изменяется и магнитный поток Ф, вследствие этого в контуре возникает электродвижущая сила (ЭДС) индукции, которая вызывает дополнительный ток (рис. 1, где 1 — проводящий замкнутый контур, 2 — силовые линии магнитного поля, создаваемого током контура). Это явление называется самоиндукцией, а дополнительный ток, вызываемый ЭДС самоиндукции, – экстратоком самоиндукции.

Явление самоиндукции наблюдается в любой замкнутой электрической цепи, в которой протекает элетрический ток, при замыкании или размыкании этой цепи.

Рассмотрим, от чего зависит величина ЭДС ε _s самоиндукции. Магнитный поток Ф, пронизывающий замкнутый проводящий контур, пропорционален магнитной индукции В магнитного поля, создаваемого током, протекающим в контуре, а индукция В пропорциональна силе тока.

Рис. 1

Тогда магнитный поток Ф пропорционален силе тока, т.е.

где L — индуктивность контура, Гн (Генри).

Индуктивностью контура L называется скалярная физическая величина, равная отношению магнитного потока Ф, пронизывающего данный контур, к величине силы тока, текущего в контуре.

Генри — это индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток 1Вб, т.е. 1 Гн = 1 .

Согласно закону электромагнитной индукции

. (3)

Подставляя (1) в (3), получим ЭДС самоиндукции:

. (4)

Формула (4) справедлива при L=const.

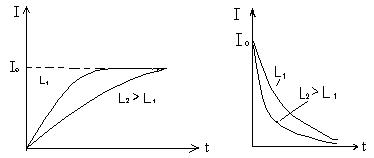
Опыт показывает, что при увеличении индуктивности L в электрической цепи сила тока в цепи увеличивается постепенно (см. рис. 2), а при уменьшении L сила тока уменьшается так же медленно (рис. 3).

Сила тока в электрической цепи при замыкании изменяется по закону 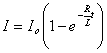, а при размыкании – по закону .

Кривые изменения силы тока показаны на рис. 2 и 3.

Рис. 2 Рис.3

Индуктивность контура зависит от формы, размеров и деформации контура, от магнитного состояния среды, в которой находится контур, а также от других факторов.

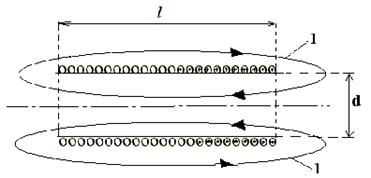
Найдем индуктивность соленоида. Соленоид — это цилиндрическая трубка, изготовленная из немагнитного непроводящего материала, на которую плотно, виток к витку, намотана тонкая металлическая проводящая проволока. На рис. 4 показан разрез соленоида вдоль цилиндрической трубки по диаметру (1 — силовые линии магнитного поля).

Рис. 4

Длина l соленоида намного больше, чем диаметр d , т.е.
l >> d . Если l d , то соленоид можно рассматривать как короткую катушку.

Диаметр тонкой проволоки намного меньше, чем диаметр соленоида. Для увеличения индуктивности внутрь соленоида помещают ферромагнитный сердечник с магнитной проницаемостью μ. Если l >>d, то при протекании тока внутри соленоида возбуждается однородное магнитное поле, индукция которого определяется формулой

где μ_о = 4π·10 -7 Гн/м – магнитная постоянная; n = N/ l – число витков единицы длины соленоида; N – число витков соленоида.

Вне соленоида магнитное поле практически равно нулю. Поскольку соленоид имеет N витков, то полный магнитный поток ψ (потокосцепление), пронизывающий поперечное сечение S соленоида, равен

где Ф = BS – поток, пронизывающий один виток соленоида.

Подставляя (5) в (6) и с учётом того, что N = n l , получим

С другой стороны,

Сравнивая (7) и (8), получим

L = μ_о μ n 2 lS = μ_о μ S . (9)

Площадь сечения соленоида равна

. (10)

С учётом (10) формула (9) запишется в виде

L = μ_о μ . (11)

Определить индуктивность соленоида можно, подключив соленоид в электрическую цепь переменного тока с частотой ω. Тогда полное сопротивление (импеданс) определится формулой

, (12)

где R – активное сопротивление, Ом; = х _L – индуктивное сопротивление; = х_с – ёмкостное сопротивление конденсатора с

Если в электрической цепи отсутствует конденсатор, т.е. электроёмкость цепи мала, то х_{с L} и формула (12) будет иметь вид

. (13)

Тогда закон Ома для переменного тока запишется в виде

, (14)

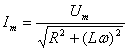
где I_m , U_m – амплитудные значения силы тока и напряжения.

Так как ω = 2πν, где ν – частота колебаний переменного тока, то (14) примет вид

. (15)

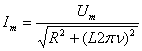
Из (15) получим рабочую формулу для определения индуктивности:

. (16)

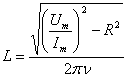
Ход работы

Для выполнения работы собрать цепь по схеме рис. 5.

1. Установить на звуковом генераторе частоту колебаний, указанную преподавателем.

2. Измерить с помощью осциллографа амплитуду напряжения U_m и частоту .

3. С помощью миллиамперметра определить действующее значение силы тока в цепи ; пользуясь соотношением и решая его относительно I_e , определить амплитуду тока в цепи.

Источник

ElectronicsBlog

Обучающие статьи по электронике

Расчёт индуктивности. Часть 2

Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Виды катушек индуктивности

Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности

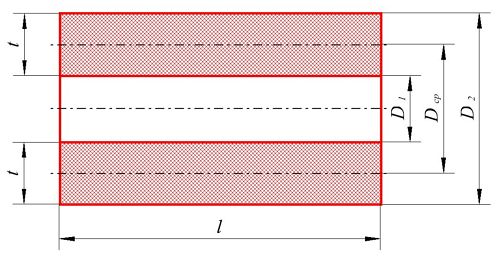
Расчёт индуктивности катушки.

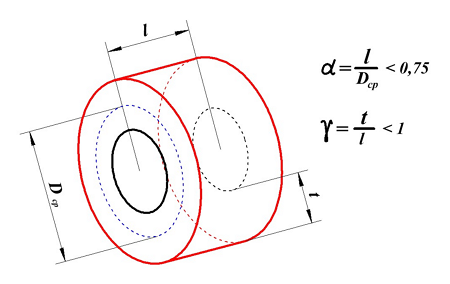
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:

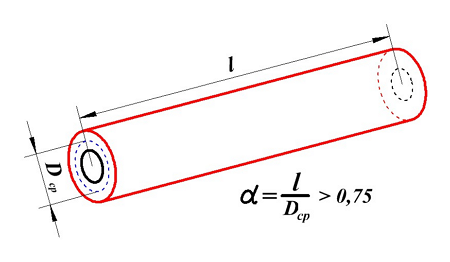
D₁ – внутренний диаметр, D₂ – внешний диаметр, D_ср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить

Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:

если l > D_ср – длинная катушка,

ω – число витков соленоида;

d – диаметр соленоида, м;

Φ – коэффициент, который зависит от отношения α = l/D;

l – длина соленоида, м;

Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d

Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит

Для короткого соленоида, то есть α -7 Гн/м;

ω – число витков соленоида;

D – средний диаметр катушки, м;

Ψ – коэффициент, который зависит от отношения ρ = t/D­;

t – толщина намотки катушки.

Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D

При небольшой толщине намотки, когда ρ 0,5

где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки

Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.

Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.

Индуктивность круговой катушки прямоугольного сечения

Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник

Индуктивность прямоугольной катушки.

Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.

Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле

где L₀ – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/D_cp;

l – длина катушки, м;

D_cp – средний диаметр катушки, м;

∆ — поправка на форму катушки.

В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру D_cp, можно разделить на несколько типов:

1. Длинная катушка, у которой α > 0,75.

2. Короткая катушка, имеющая α 1.

Рассмотрим каждый случай по отдельности.

Индуктивность длинной катушки

Для длинной катушки (α > 0,75) величина L₀ рассчитывается также как для длинного соленоида, где l – длина соленоида, D_cp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

где D₁ – внутренний диаметр, D₂ – внешний диаметр.

Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром D_CP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.

Индуктивность короткой катушки

Для короткой катушки (α l) величина L₀ рассчитывается также как для плоской катушки, где t – толщина намотки, D_cp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ -7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности L_P

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

где p – шаг намотки по длине катушки, s_p – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

где q – шаг намотки по толщине катушки, s_p – диаметр голого провода (без изоляции).

Расчёт поправки на взаимную индуктивность витков

В общем случае поправка на взаимную индуктивность витков ∆₂L катушки определяется выражением

где μ₀ – магнитная постоянная, μ₀ = 4π•10 -7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

J – коэффициент, зависящий формы катушки и от числа витков катушки.

1. Для катушки выполненной в один слой по длине катушки (соленоид):

а) при определении расчётной индуктивности L_P толщина намотки t принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит

где ω – количество витков катушки.

2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):

а) при определении расчётной индуктивности L_P длина катушки l принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит

где ω – количество витков катушки.

На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник