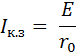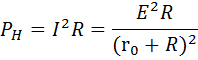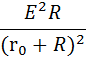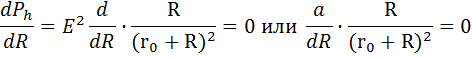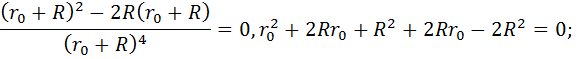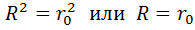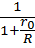Выведите условие максимальной полезной мощности

Полная и полезная мощность. Коэффициент полезного действия (к. п. д. )

Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.

Она определяется по формуле

Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.

Обычно электрический к. п. д. принято выражать в процентах.

Для практической электротехники особый интерес представляют два вопроса:

1. Условие получения наибольшей полезной мощности

2. Условие получения наибольшего к. п. д.

Условие получения наибольшей полезной мощности (мощности в нагрузке)

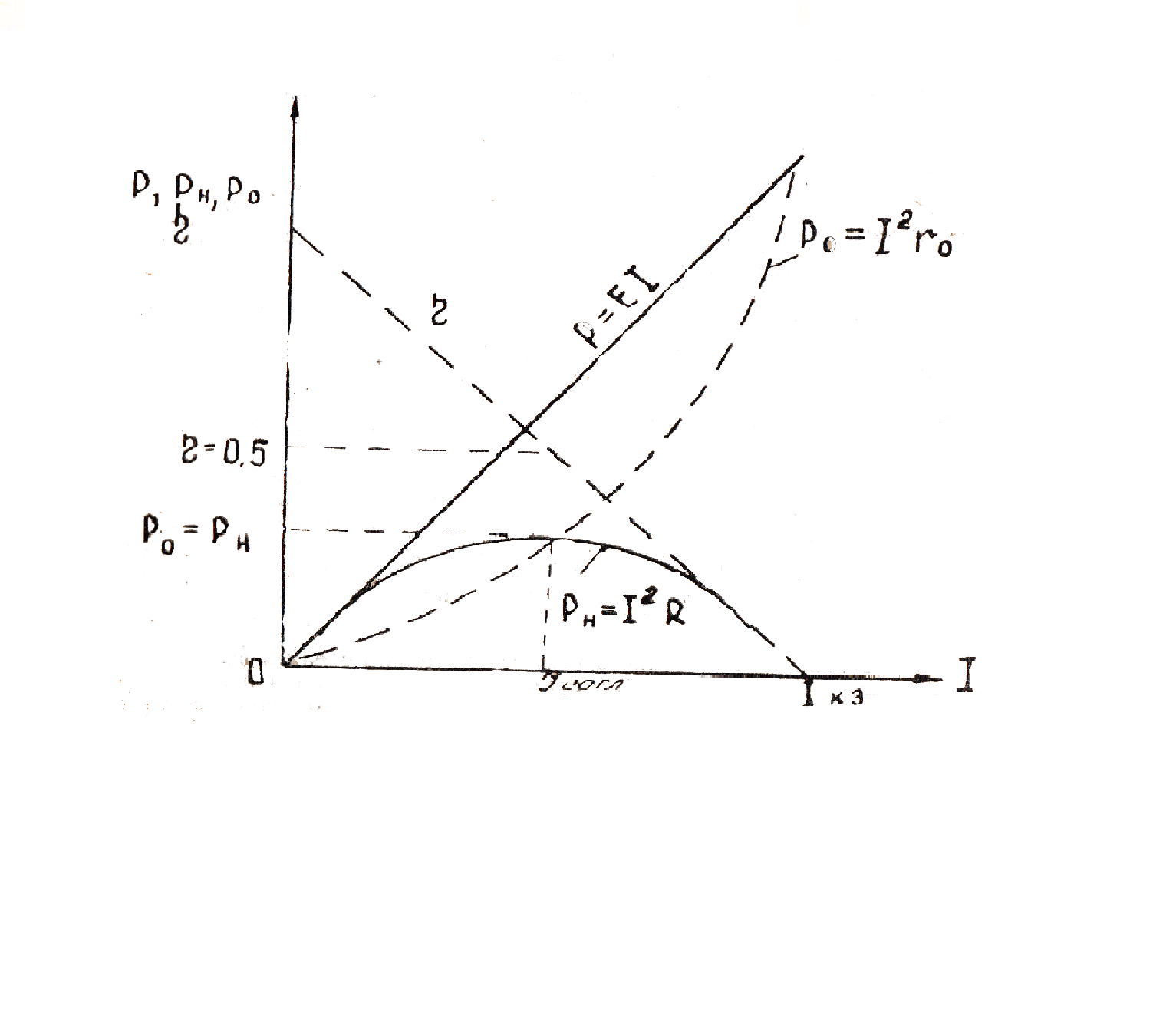
Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.

Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.

Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.

Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.

Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.

Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.

Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.

Условие получения наибольшего к. п. д коэффициента полезного действия

Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).

По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.

В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).

Подводя итоги вышеизложенному, можно сделать выводы.

Условие получения максимальной полезной мощности( R=R₀) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.

В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).

Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.

Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.

Источник

Условие передачи максимума мощности от источника

В нагрузку

Из формулы закона Ома для всей цепи (1.5) э.д.с. источника рав­на сумме падений напряжений на внешнем участке цепи U и внут­ри источника Uo = I ;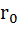

Умножив обе части равенства на величину тока I, получим ypaвнение баланса мощностей (1.17)

EI = I 2 r₀+I 2 R или Рист. = Р₀ + Рн 1. 18

Из уравнения (1. 18) видно, что мощность, отдаваемая источни­ком, состоит из мощности потерь внутри источника Р₀ и мощно­сти, потребляемой нагрузкой Рн. Исследуем зависимость мощноcти ,передаваемой в нагрузку и к.п.д. источника от величины со- противления внешней цепи R (от величины тока в цепи I).

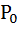
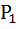
В режиме холостого хода (R = ∞) ток в цепи отсутствует (1=0), а поэтому мощности Р, и равны нулю.

В режиме короткого замыкания (R=0) ток в цепи достигает мл к си малым, но значения

При этом источник отдает максимальную мощность, которая полностью расходуется внутри самого источника, так как мощность, развиваемая во внешней цепи (в нагрузке равна нулю)

Мощность, развиваемая током в нагрузке, определяется выражением

и будет иметь максимальное значение, когда дробь

Считая сопротивление внешнего участка Цепи (нагрузки) R переменной величиной, найдем условие максимума функции. Pn=f(R)

Нa основании полученного результата можно сделать вывод, что условием передачи максимума мощности от источника в нагрузку (во внешнюю цепь) является равенство внутреннего сопротивления источника и сопротивления нагрузки (внешнего участка цепи), Следовательно, внешняя Цепь и источник работают в согласован­ном режиме при R= .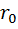

Коэффициент полезного действия (к.п.д.) источника определим как отношение мощности внешней цепи к мощности источника

= = =

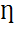
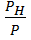
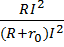
Из равенства (1.20) видно, что в режиме холостого хода к.п.д. источники равен единице 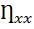= 1 ; в режиме короткого замыкания

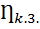
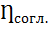
при R=0 = 0 и в режиме согласованной нагрузки при R = r₀ = 0,5

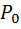
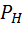
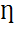
На графике рис. 12 показана зависимость Рист ., , и от тока в цепи I.

На практике согласованный режим применяется только тогда, когда низкий к.п.д. (0,5) не имеет решающего значения из-за ма­лой мощности цепи и когда вопрос максимальной мощности имёет большее значение, чем вопрос экономического порядка (радиотех­нические цепи, электропроводная связь, автоматика и т.п.) — При пе­редаче больших мощностей, когда вопросы экономики являются весьма существенными, используются режимы с более высоким к.п.д. Для этого внутреннее сопротивление источника должно быть значительно меньше сопротивления нагрузки (внешней цепи). В этих случаях номинальный режим работы источника близок к ре­жиму холостого хода, а к.п.д. источника близок к единице.

Дата добавления: 2016-04-06 ; просмотров: 2696 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Формула полезной мощности

Определение и формула полезной мощности

Мощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.

Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:

\[\left\langle P\right\rangle =\frac<\Delta A><\Delta t>\left(1\right).\]

Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:

Приняв во внимание, что:

\[\Delta A=\overline\cdot \Delta \overline\left(3\right),\]

где $\Delta \overline$ — перемещение тела под действием силы $\overline$, в выражении (2) имеем:

где $\ \overline-$ мгновенная скорость.

Коэффициент полезного действия

При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:

где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:

\[P_p=\eta P\ \left(6\right).\]

Формула полезной мощности источника тока

Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:

где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.

Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:

где $P_p=UI=I^2R=\frac(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:

Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50\% общей мощности.

При коротком замыкании (когда $R\to 0;;U\to 0$) или в режиме холостого хода $(R\to \infty ;;I\to 0$) полезная мощность равна нулю.

Примеры задач с решением

Задание. Коэффициент полезного действия электрического двигателя равен $\eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?

Решение. За основу решения задачи примем формулу:

\[P_p=\eta P\ \left(1.1\right).\]

Полную мощность найдем, используя выражение:

Подставляя правую часть выражения (1.2) в (1.1) находим, что:

Вычислим искомую мощность:

\[P_p=\eta IU=0,42\cdot 110\cdot 10=462\ \left(Вт\right).\]

Ответ. $P_p=462$ Вт

Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.

Решение. По закону Ома для цепи с источником тока мы имеем:

где $\varepsilon$ — ЭДС источника тока; $r$ — его внутреннее сопротивление.

При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:

Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:

Тогда сила тока в цепи равна:

Максимальную полезную мощность найдем, используя формулу:

Мы получили систему из трех уравнений с тремя неизвестными:

Используя первое и второе уравнения системы (2.6) найдем $I’$:

Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:

\[\varepsilon=I\left(R+r\right);;\ I_kr=\varepsilon \to I\left(R+r\right)=I_kr\to r\left(I_k+I\right)=IR\to r=\frac\left(2.8\right).\]

Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:

Источник

Выведите условие максимальной полезной мощности

ЛАБОРАТОРНАЯ РАБОТА № 3.7.

ИССЛЕДОВАНИЕ ПОЛЕЗНОЙ МОЩНОСТИ И КПД ИСТОЧНИКОВ ТОКА

Фамилия И.О. _____________ Группа ______ Дата ______

Цель данной работы – экспериментально проверить теоретические выводы о зависимости полезной мощности и КПД источника тока от сопротивления нагрузки.

Электрическая цепь состоит из источника тока, подводящих проводов и нагрузки или потребителя тока. Каждый из этих элементов цепи обладает сопротивлением.

Сопротивление подводящих проводов обычно бывает очень мало, поэтому им можно пренебречь. В каждом участке цепи будет расходоваться энергия источника тока. Весьма важное практическое значение имеет вопрос о целесообразном расходовании электрической энергии.

Полная мощность Р, выделяемая в цепи, будет слагаться из мощностей, выделяемых во внешней и внутренней частях цепи: P = I 2 ·R + I 2 ·r = I 2 (R + r). Так как I(R + r) = ε, то Р =I·ε,

где R – внешнее сопротивление; r – внутреннее сопротивление; ε – ЭДС источника тока.

Таким образом, полная мощность, выделяемая в цепи, выражается произведением силы тока на ЭДС элемента. Эта мощность выделяется за счет каких-либо сторонних источников энергии; такими источниками энергии могут быть, например, химические процессы, происходящие в элементе.

Рассмотрим, как зависит мощность, выделяемая в цепи, от внешнего сопротивления R, на которое замкнут элемент. Предположим, что элемент данной ЭДС и данного внутреннего сопротивления r замыкается внешним сопротивлением R; определим зависимость от R полной мощности Р, выделяемой в цепи, мощности Р_а, выделяемой во внешней части цепи и КПД.

Сила тока I в цепи выражается по закону Ома соотношением

Полная мощность, выделяемая в цепи, будет равна

При увеличении R мощность падает, стремясь асимптотически к нулю при неограниченном увеличении R.

Мощность, выделяющаяся во внешней части цепи, равна

Отсюда видно, что полезная мощность Р_а равна нулю в двух случаях – при R = 0 и R = ∞.

Исследуя функцию Р_а = f(R) на экстремум, получим, что Р_а достигает максимума при R = r, тогда

Чтобы убедится в том, что максимум мощности Р_а получается при R = r, возьмем производную Р_а по внешнему сопротивлению

По условию максимума требуется равенство нулю первой производной

r 2 = R 2

R = r

Можно убедиться, что при этом условии мы получим максимум, а не минимум для Р_а, определив знак второй производной .

Коэффициент полезного действия (КПД) η источника ЭДС это величина отношения мощности Р_а, выделяющейся во внешней цепи, к полной мощности Р, развиваемой источником ЭДС.

В сущности КПД источника ЭДС указывает, какая доля работы сторонних сил преобразуется в электрическую энергию и отдается во внешнюю цепь.

Выражая мощность через силу тока I, разность потенциалов во внешней цепи U и величину электродвижущей силы ε, получим

То есть КПД источника ЭДС равен отношению напряжения во внешней цепи к ЭДС. В условиях применимости закона Ома можно далее заменить U = IR; ε = I(R + r), тогда

Следовательно, в том случае, когда вся энергия расходуется на Ленц-Джоулево тепло, КПД источника ЭДС равен отношению внешнего сопротивления к полному сопротивлению цепи.

При R = 0 имеем η = 0. С увеличением R, КПД возрастает, стремится к значению η=1 при неограниченном увеличении R, однако при этом мощность, выделяющаяся во внешней цепи, стремится к нулю. Таким образом, требования одновременного получения максимальной полезной мощности при максимальном КПД невыполнимы.

Когда Р_а достигает максимума, то η = 50%. Когда же КПД η близок к единице, полезная мощность мала по сравнению с максимальной мощностью, которую мог бы развивать данный источник. Поэтому для увеличения КПД необходимо по возможности уменьшать внутреннее сопротивление источника ЭДС, например, аккумулятора или динамо-машины.

В случае R = 0 (короткое замыкание) Р_а = 0 и вся мощность выделяется внутри источника. Это может привести к перегреву внутренних частей источника и выводу его из строя. По этой причине короткие замыкания источников (динамо-машины, аккумуляторные батареи) недопустимы!

На рис. 1 кривая 1 дает зависимость мощности Р_а, выделяемой во внешней цепи, от сопротивления внешней части цепи R; кривая 2 дает зависимость от R полной мощности Р; кривая 3 – ход КПД η от того же внешнего сопротивления.

Порядок выполнения работы

1. Ознакомиться со схемой на стенде.

2. Установить с помощью магазина сопротивление R = 100 Ом.

3. Замкнуть ключ К.

4. Произвести измерения силы тока в цепи последовательно для различных девяти сопротивлений на магазине сопротивлений, начиная от 100 Ом и выше. Внести в таблицу результаты измерений силы тока, выразив их в амперах.

5. Выключить ключ К.

6. Вычислить для каждого сопротивления Р, Р_а (в ваттах) и η.

7. Построить графики Р, Р_а и η от R.

1. Что называется КПД источника ЭДС?

2. Вывести формулу КПД источника ЭДС.

3. Что такое полезная мощность источника ЭДС?

4. Вывести формулу полезной мощности источника ЭДС.

5. Чему равна максимальная мощность, выделяемая во внешней цепи (Ра)max?

6. При каком значении R полная мощность Р, выделяющаяся в цепи, максимальна?

7. Чему равен КПД источника ЭДС при (Ра)max?

8. Произвести исследование функции (Ра) = f(R) на экстремум.

9. Зарисовать график зависимости Р, Ра и η от внешнего сопротивления R.

10. Что такое ЭДС источника?

11. Почему сторонние силы должны быть не электрического происхождения?

12. Почему недопустимо короткое замыкание для источников напряжения?

, Вт

, Вт

Источник