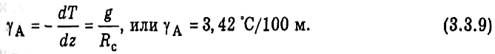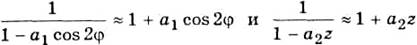- Вывести барометрическую формулу т е получить закон изменения давления атмосферы с увеличением высоты
- Зависимость давления от высоты: барометрическая формула
- Что такое воздух?
- Давление воздуха
- Зависимость давления от высоты
- Пример решения задачи
- Интегрирования уравнения статики. Барометрические формулы.
- Барометрические формулы
Вывести барометрическую формулу т е получить закон изменения давления атмосферы с увеличением высоты
В данном разделе мы выведем зависимость давления газа \(P\) от высоты \(h\) над уровнем моря в гравитационном поле Земли.
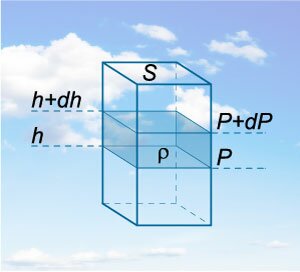
Возьмем произвольную цилиндрическую колонну газа с площадью сечения \(S\) и высотой \(h.\) Вес выделенного объема газа будет равен \[F = mg = \rho gV = \rho ghS,\] где \(\rho\) означает плотность газа. Плотность газа будет выражаться следующей формулой: \[\require = \frac<<\rho gh\cancel>><\cancel> = \rho gh. \] Теперь представим такую колонну в атмосфере и выделим в ней тонкий слой воздуха высотой \(dh\) (рисунок \(1\)). Ясно, что такой слой вызывает изменение давления на величину \[dP = — \rho gdh.\] Мы поставили здесь знак минус, поскольку давление должно уменьшаться с увеличением высоты.
Рассматривая атмосферный воздух как идеальный газ, воспользуемся уравнением Менделеева-Клапейрона, чтобы выразить плотность \(\rho\) через давление \(P:\) \[
Таким образом, зависимость атмосферного давления от высоты выражается формулой: \[P =
Если давление определяется в миллиметрах ртутного столба \(\left( \text <мм.рт.ст.>\right),\) то барометрическая формула принимает вид: \[P\left( h \right) = 760\exp \left( < - 0.00012\,h>\right)\;\left[ \text <мм.рт.ст.>\right].\] Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения.
Давление воздуха в шахте можно оценить, используя общую барометрическую формулу : \[P =
После несложных вычислений находим: \[
\exp \left( < - \frac<
Источник
Зависимость давления от высоты: барометрическая формула
Многие люди знают, что с увеличением высоты уменьшается давление воздуха. Рассмотрим вопрос, почему давление воздуха уменьшается с высотой, приведем формулу зависимости давления от высоты, а также рассмотрим пример решения задачи с использованием полученной формулы.
Что такое воздух?
Воздух — это бесцветная смесь газов, которая составляет атмосферу нашей планеты. В его состав входят множество различных газов, основными из которых являются азот (78 %), кислород (21 %), аргон (0,9 %), углекислый газ (0,03 %) и другие.
С точки зрения физики поведение воздуха при существующих условиях на Земле подчиняется законам идеального газа — модели, согласно которой молекулы и атомы газа не взаимодействуют друг с другом, расстояния между ними огромные по сравнению с их размерами, а скорости движения при комнатной температуре составляют порядка 1000 м/с.
Давление воздуха
Рассматривая вопрос зависимости давления от высоты, следует разобраться, что представляет собой концепция «давление» с физической точки зрения. Под давлением воздуха понимают силу, с которой воздушный столб давит на поверхность. В физике она измеряется в паскалях (Па). 1 Па означает, что сила в 1 ньютон (Н) перпендикулярно приложена к поверхности площадью 1 м 2 . Таким образом, давление 1 Па — это очень маленькое давление.
На уровне моря давление воздуха составляет 101 325 Па. Или, округляя, 0,1 МПа. Это значение принято называть давлением 1 атмосферы. Приведенная цифра говорит, что на площадку 1 м 2 воздух давит с силой 100 кН! Это большая сила, однако человек ее не ощущает, так как внутри него кровь создает аналогичное давление. Кроме того, воздух относится к текучим веществам (к ним также относятся жидкости). А это значит, что он оказывает по всем направлениям одинаковое давление. Последний факт говорит о том, что давление атмосферы с разных сторон на человека взаимно компенсируется.
Зависимость давления от высоты
Атмосферу около нашей планеты держит земная гравитация. Гравитационные силы также являются виновником падения давления воздуха с увеличением высоты. Справедливости ради следует отметить, что не только земное притяжение приводит к уменьшению давления. А также снижение температуры тоже вносит свой вклад.
Поскольку воздух является текучим веществом, тогда для него можно использовать гидростатическую формулу зависимости давления от глубины (высоты), то есть ΔP = ρ*g*Δh, где: ΔP — величина изменения давления при изменении высоты на Δh, ρ — плотность воздуха, g — ускорение свободного падения.
Учитывая, что воздух является идеальным газом, из уравнения состояния идеального газа следует, что ρ = P*m/(k*T), где m — масса 1 молекулы, T — его температура, k — постоянная Больцмана.
Объединяя две приведенные выше формулы и решая полученное уравнение относительно давления и высоты, можно получить следующую формулу: Ph = P0*e -m*g*h/(k*T) , где Ph и P0 — давление на высоте h и на высоте уровня моря, соответственно. Полученное выражение называется барометрической формулой. Она может использоваться для расчетов зависимости атмосферного давления от высоты.
Иногда для практическим целей необходимо решать обратную задачу, то есть находить высоту, зная давление. Из барометрической формулы легко можно получить зависимость высоты от уровня давления: h = k*T*ln(P0/Ph)/(m*g).
Пример решения задачи
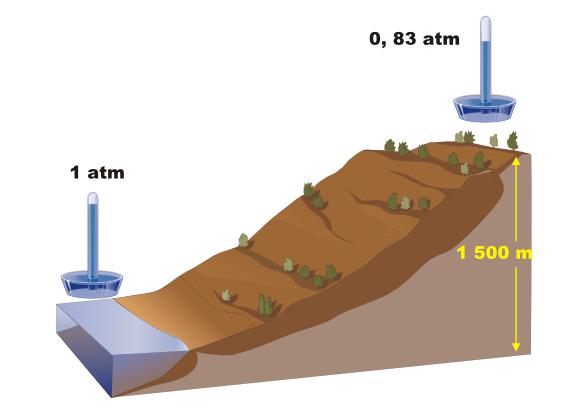
Боливийский город Ла-Пас является самой «высокой» столицей в мире. Из разных источников следует, что город расположен на высоте от 3250 метров до 3700 метров над уровнем моря. Задача состоит в расчете давления воздуха на высоте Ла-Пас.
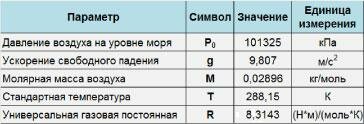
Для решения задачи воспользуемся формулой зависимости давления от высоты: Ph = P0*e -m*g*h/(k*T) , где: P0 = 101 325 Па, g = 9,8 м/с 2 , k = 1,38*10 -23 Дж/К, T = 293 K (20 o C), h = 3475 м (среднее между 3250 м и 3700 м), m = 4,817*10 -26 кг (с учетом молярной массы воздуха 29 г/моль). Подставляя цифры, получаем: Ph = 67 534 Па.
Таким образом, давление воздуха в столице Боливии составляет 67 % от давления на уровне моря. Низкое давление воздуха является причиной головокружений и общей слабости организма, когда человек поднимается в горные районы.
Источник
Интегрирования уравнения статики. Барометрические формулы.
Интегралы основного уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой, носят общее название барометрических формул. На основе баром-ских формул решаются такие важные практические задачи, как расчет распределения давления и плотности по высоте, определение высот различных летательных аппаратов по измеренному давлению, приведение давления к уровню моря и др.Для получения интегральной формы основного урав-ния статики проинтегрируем левую и правую части в пределах от уровня моря z=0 (или земной поверхности),где давление р 
ln p = ln p0 – 
Прежде чем рассматривать общий случай, рассмотрим несколько частных случаев, отличающихся один от другого различными предположениями относительно вида функций Т=Т(z) или р=р(z), с помощью которых описывается распределение температуры или плотности по высоте. Эти частные случаи являются своеобразными предельными случаями для реальной атмосферы.
Однородная атмосфера. Предположим, что плотность воздуха в пределах всей атмосферы не изменяется с высотой р = р0 = const,где ро—плотность воздуха при z=0. Такая атмосфера носит название однородной. Пренебрежем зависимостью ускорения силы тяжести от высоты получим барометрическую формулу однородной атмосферы (О. А.): p=p0-gρ0dz
Согласно этой ф-ле, давление в О.А. падает с высотой по линейному закону: на сколько возрастав высота, па столько же падает и давление (рис). Отметим, что в приложении к атмосфере формула дает заведомо далекое о реальных условий распределение давлена Но для гидросферы, плотность которой из меняется в очень узких пределах (плотность воды близка 1 г/см3), формула дает вполне удовлетворительные результаты. Поэтому ее можно назвать баром-ской ф-лой гидросферы. Поставим вопрос о высоте О.А., т. е. такой высоте, на которой давление обращается в нуль (р = 0). Обозначим ее через Н. Имеем 0= p0-gρ0H или H= p0/ gρ0. Так как p0/ ρ0= RcT0, где Т0 тем-ра воздуха при z=0, то формула приним вид: H= RcT0/g=273 Rc/g(1+αt0).Отсюда следует, что высота О.А. конечна и зависит только от тем-ры воздуха на поверхности 3емли. При t0=0° она составляет Н0=273 Rc/g=273*276/981=7990=8000 м. Поскольку плотность в О.А. постоянна давление быстро падает с высотой, то тем-ра ее, равная по уравнению состояния T=p/ Rc ρ0,должна понижаться. Беря производную по высоте от левой и правой частей, получаем dT/dz=1/Rc ρ0*dp/dz. находим следующее выражение для вертикального градиента температуры (уA) в О.А:yA = -dT/dz=g/Rc=3,42 град/100 м. Таким образом, в однородной атмосфере температура падает с высотой по линейному закону Т= Т0 — уAz,при этом скорость падения (градиент) значительно больше среднего значения у в пределах тропосферы. Вертикальный градиент температуры уA в О.А. получил название градиента автоконвекции. Изменение плотности воздуха с высотой. В связи с введением понятия градиента автоконвекции рассмотрим вопрос об изменении плотности воздуха с высотой в общем случае. С этой целью возьмем так называемую логарифмическую производную по высоте от левой я правой частей уравнения состояния 1/p*dp/dz=1/p*dρ/dz+1/T*dT/dz. Заменяя dp/dz: 1/ρ*d ρ /dz=-1/T(g/Rc+dT/dz), или 1/ρ*d ρ /dz=1/T(y-yA). Формула (З.Н) справедлива для любого распределения тем-ры воздуха с высотой. На основе ее можно сделать выводы относительно изменения плотности воздуха с высотой. Возможны три различных случая. а) Если у> yA=3,42град/м, т. е. плотность воздуха возрастает с высотой. Вертикальные градиенты температуры у больше, чем 3,42 град/100 м, в реальных условиях атмосферы могут наблюдаться лишь в дневные часы (летом) в приземном слое атмосферы. Такое состояние атмосферы является, очевидно, сильно неустойчивым: небольшое возмущение приведет к тому, что верхние более плотные частицы начнут опускаться вниз, а нижние более легкие — подниматься вверх: возникнет движение воздуха, называемое конвекцией. Отсюда и название у —градиент автоконвекции. б) Если у= yA, то dp/dz =0, т. е. плотность воздуха не изменяется с высотой: р = р0 = const . Это — случай однородной атмосферы. в) Если y
Источник
Барометрические формулы
Уравнение статики является одним из важнейших уравнений метеорологии, на основе которого устанавливаются закономерности распределения давления, плотности и массы воздуха по высоте. В своем дифференциальном виде уравнение статики (3.2.4) позволяет выполнить расчет изменения давления лишь для малых приращений высоты dz.
На практике всегда необходимо иметь данные о распределении давления в слоях атмосферы конечной толщины или определить толщину таких слоев по измеренным значениям давления. Для этой цели уравнение статики следует записать в конечном (интегральном) виде, т. е. найти его интегралы. Интегралы уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой, носят общее название барометрических формул. На основе барометрических формул решаются такие важные практические задачи, как расчет распределения давления и плотности по высоте, определение высоты различных летательных аппаратов по измеренному давлению, приведение давления к уровню моря и др.
Для получения интегральной формы уравнения статики проинтегрируем левую и правую части (3.2.4) в пределах от уровня моря 2=0 (или земной поверхности), где давление р0, до произвольной высоты г, где давление р. Имеем
Здесь ρ = ρ(z) – функция высоты
Другую интегральную форму уравнению статики можно придать, если воспользоваться уравнением состояния влажного воздуха (1.4.12) из главы 1. Подставив найденное отсюда значение р, перепишем (3.2.4) в виде

Интегрируя в пределах от 0 до z и от р0 до р, получаем:
Интегральные формы (3.3.1) и (3.3.3) уравнения статики в дальнейшем широко используются для получения различных барометрических формул. Заметим, что p0 в формулах (3.3.1) и (3.3.3) может обозначать давление как на уровне моря, так и на поверхности Земли. Различие будет состоять лишь в начале отсчета высоты г. В общем случае температура, а вместе с ней и плотность воздуха являются достаточно сложными функциями высоты, установить аналитический вид которых не всегда представляется возможным. Поэтому прежде чем перейти к общему случаю, рассмотрим несколько частных случаев, отличающихся один от другого различными предположениями относительно вида функций Т = T(z) или р = р(z), с помощью которых описывается распределение температуры или плотности по высоте.
Однородная атмосфера. Предположим, что плотность воздуха в пределах всей атмосферы
не изменяется с высотой, т. е.
Здесь р0— плотность воздуха при z = 0. Такая атмосфера носит название однородной. Пренебрежем зависимостью ускорения свободного падения от высоты. Тогда на основании (3.3.1) получаем барометрическую формулу однородной атмосферы:
Согласно этой формуле, давление в однородной атмосфере убывает с высотой по линейному закону (рис. 3.2).

Поставим вопрос о высоте однородной атмосферы, т. е. такой высоте, на которой давление обращается в нуль (р = 0).
Обозначим ее через Н. Согласно (3.3.5), имеем
Поскольку в соответствии с уравнением (1.3.8) р0/ρ0 = RcT0 (T0— температура воздуха при z = 0), формула (3.3.6) принимает вид
Отсюда следует, что высота однородной атмосферы конечна и зависит только от
температуры воздуха на поверхности Земли. При Т = О °С она составляет
Поскольку плотность в однородной атмосфере постоянна, а давление быстро убывает с высотой, температура ее, равная в соответствии с уравнением состояния
должна понижаться. Если взять производную по высоте от левой и правой части (3.3.8), то получим:
Привлекая (3.2.5), находим следующее выражение для вертикального градиента температуры
уА в однородной атмосфере:
Таким образом, в однородной атмосфере температура убывает с высотой по линейному закону:
при этом скорость понижения температуры (градиент) значительно больше среднего значения у в пределах тропосферы.
Изменение плотности воздуха с высотой. Рассмотрим вопрос об изменении плотности воздуха с высотой в общем случае. С этой целью сначала прологарифмируем, а затем продифференцируем по высоте левую и правую часть уравнения состояния (1.3.8):
Заменив dp/dz в соответствии с (3.2.5) и подставив в полученное выражение р из уравнения (1.3.8), найдем:
Формула (3.3.11) справедлива для любого распределения температуры воздуха по высоте. На основе ее можно сделать выводы относительно изменения плотности воздуха с высотой. Возможны три различных случая.
1. Если γ > γА= 3,42 o С/100 м, то dρ/dz > 0, т. е. плотность воздуха возрастает с высотой. Вертикальные градиенты температуры γ, превышающие 3,42 o С/100 м, в реальных условиях атмосферы могут наблюдаться лишь в дневные часы (летом) в приземном слое атмосферы. При таких условиях плотность в этом слое увеличиваетсяс высотой.
2. Если γ = γА, то dρ/dz = 0, т. е. плотность воздуха не изменяется с высотой (постоянна): ρ = ρ0 = const. Это случай однородной атмосферы.
3. Если γ γА. Таким образом, наиболее характерным состоянием атмосферы является такое, когда плотность воздуха убывает с высотой.
Изотермическая атмосфера. Атмосфера называется изотермической, если температура не изменяется с высотой, т. е.
Т = То = const,
где То — температура на уровне моря или поверхности Земли. Изотермическая атмосфера по своим свойствам во многом противоположна однородной атмосфере. Считая атмосферу сухой и пренебрегая зависимостью ускорения свободного падения от высоты, на основании (3.3.3) и последнего соотношения получаем барометрическую формулу изотермической атмосферы:
Давление в изотермической атмосфере убывает с высотой по экспоненциальному (показательному) закону
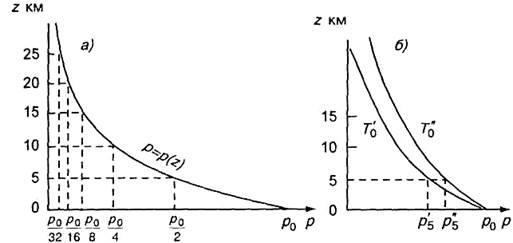
Графически зависимость давления р от высоты z в изотермической атмосфере представлена на рис. 3.3. Рисунок 3.3 а поясняет вытекающую из формулы (3.3.12) закономерность: если высота возрастает в прогрессии арифметической, то давление убывает в прогрессии геометрической. Кривые на рис. 3.3 б соответствуют различным температурам атмосферы (постоянным по высоте): T ′′ 0 > T ′ 0. Из этого рисунка и анализа формулы (3.3.12) следует, что при одном и том же давлении у земной поверхности давление на высотах (например 5, 10, 15 км) при температуре T ′′ 0 больше, чем при T ′ 0. Одно и то же значение давления наблюдается при температуре T ′′ 0 на более высоких уровнях, чем при температуре T ′ 0. Это означает, что при более высокой температуре давление в изотермической атмосфере убывает с высотой медленнее, чем при более низкой температуре.
Абсолютное значение убывания давления в слоях равной толщины в нижней части атмосферы больше, чем в верхней. Так, в слое от О до 5 км давление при средних условиях падает на p0 — p0/2 = p0/2, т. е. примерно на 500 гПа (при р0 = 1000 гПа); в слое от 5 до 10 км падение давления составляет р0/2 — р0/4 = р0/4 т. е. около 250 гПа, а в слое от 20 до 25 км давление уменьшается всего лишь на р0/16 — р0/32 = р0/32, т. е. примерно на 31—32 гПа. Таким образом, чем выше расположен слой атмосферы определенной толщины, тем меньше падение давления в этом слое.
Рис. 3.3. Распределение давления по высоте в изотермической атмосфере.
а — общая закономерность падения давления, б — падение давления при разных температурах (T ′′ 0 > T ′ 0).
Высота изотермической атмосферы равна бесконечности, т. е. р → 0 только при z → ∞.
Формула для плотности воздуха может быть получена, если обратиться к уравнению состояния, согласно которому
Поскольку в изотермической атмосфере Т/Т0 =1, то на основании (3.3.12) получаем
Величина δ = ρ/ρо носит название относительной плотности.
Политропная атмосфера. Политропной называют такую атмосферу, которая характеризуется линейным изменением температуры с высотой (или постоянным значением вертикального градиента температуры):
Считая атмосферу сухой (Tυ = Т) и подставляя Т в соответствии с (3.3.14) в формулу (3.3.3), получаем:
Выполнив интегрирование (в предположении g — const), приходим к барометрической формуле политропной атмосферы:
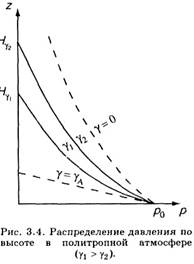
Графически зависимость р от z изображена на рис. 3.4. Кривые соответствуют одним и тем же значениям р0 и T0, но различным значениям вертикального градиента температуры: γ1 и γ2. Давление при большем значении вертикального градиента температуры (γ1) убывает с высотой быстрее, чем при меньшем (γ2). Для сравнения на рис. 3.4 приведены кривые изменения давления в однородной и изотермической атмосферах (штриховые кривые). Высота политропной атмосферы конечна. В самом деле, согласно (3.3.15), давление обращается в нуль на такой высоте z = Нγ, на которой
Высота политропной атмосферы изменяется в широких пределах; при Т0 = 288 К и γ = 0,65 К/100 м значение Нγ составляет 44,3 км.
Формула для плотности воздуха в политропной атмосфере имеет вид
Полная барометрическая формула (формула Лапласа).
Рассмотрим общий случай, т. е. случай произвольного распределения температуры по высоте. Учтем также, что реальный воздух влажный, а ускорение свободного падения — функция широты и высоты. Привлекая соотношение (3.1.2) и учитывая, что
уравнение (3.3.2) перепишем в виде
(вследствие малости слагаемых а1 cos 2φ> и a2z по сравнению с единицей), то формулу (3.3.18) приведем к виду
где H0 = 273Rc/g0 — высота однородной атмосферы при t = 0 °С.
Проинтегрируем (3.3.19) в пределах от высоты z1, где давление равно p1, до высоты z2, где давление равно р2. Для величин t, s и z в правой части (3.3.19) при интегрировании введем средние значения (на основании известной теоремы о среднем). Выполнив интегрирование, получим:
полная барометрическая формула (формула Лапласа) окончательно принимает вид
Величина В = 2,30Н0 ≈ 18 400 м называется барометрической постоянной, а средние значения 

В таком полном виде барометрическая формула на практике используется лишь при барометрическом нивелировании. При решении подавляющего большинства метеорологических задач такой высокой точности, какую может обеспечить формула Лапласа, не требуется. К тому же следует иметь в виду, что точность измерения исходных данных (температуры, влажности, давления), необходимых для выполнения расчетов по формуле (3.3.21), как правило, значительно меньше тех уточнений, которые дает формула Лапласа по сравнению с приводимой ниже барометрической формулой реальной атмосферы. Последняя получается из формулы (3.3.21), если считать воздух сухим (s = 0) и пренебречь зависимостью ускорения свободного падения от широты и высоты:
Возвращаясь к натуральным логарифмам и абсолютной температуре, формулу (3.3.22) можно переписать в виде
где 

Средняя барометрическая температура — это такая постоянная в пределах слоя температура, которая обеспечивает значения давления на границах его, наблюдаемые при реальном распределении температуры по высоте. Практически Т нередко отождествляют со средней арифметической температурой, т. е. полагают
где Т1 и Т2 — температуры воздуха на нижней и верхней границах слоя. Если уровень z1 совпадает с поверхностью Земли (z1 = 0), а уровень z2 — произвольный (z2 = z), то формула (3.3.23) принимает вид
Эта формула имеет такой же вид, как и барометрическая формула (3.3.12) изотермической атмосферы. Принципиальное различие состоит в том, что формулы (3.3.20), (3.3.23) и (3.3.25) всегда справедливы лишь для слоя заданной конечной толщины, для которого температура 


Если необходимо учесть влияние влажности на плотность воздуха и распределение давления по высоте, то в формулах (3.3.22) — (3.3.25) средняя барометрическая температура 

Источник