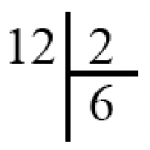Вывести число двоичной форме

Вывести целое число в двоичном формате на Java

У меня есть номер, и я хочу напечатать его в двоичном виде. Я не хочу делать это, написав алгоритм. Есть ли встроенная функция для этого в Java?

Предполагая, что вы имеете в виду «встроенный»:

( Long имеет аналогичный метод, BigInteger имеет метод экземпляра, где вы можете указать основание.)

Здесь нет необходимости зависеть только от двоичного или любого другого формата . доступна одна гибкая встроенная функция, которая печатает любой формат, который вы хотите в вашей программе. Integer.toString (int, presentation);

Мне нужно было что-то, чтобы красиво распечатать вещи и разделить биты каждый n-бит. Другими словами, отобразить начальные нули и показать что-то вроде этого:

Итак, вот что я написал:

Вызовите это так:

проверить эту логику можно преобразовать число в любую базу

ИЛИ

Это самый простой способ печати внутреннего двоичного представления целого числа. Например : если мы возьмем n как 17, то результат будет: 0000 0000 0000 0000 0000 0001 0001

Просто попробуйте. Если область видимости печатает только двоичные значения заданного целочисленного значения. Это может быть положительным или отрицательным.

вход

Вывод

Решение с использованием 32-битной маски дисплея,

Простое и довольно простое решение.

Здесь уже есть хорошие ответы на этот вопрос. Но я попробовал именно так (и, может быть, это самая простая логика на основе → по модулю / делить / добавить ):

Вопрос сложен в Java (и, вероятно, также на другом языке).

Целое число представляет собой 32-битный подписанный тип данных, но Integer.toBinaryString () возвращает строковое представление целочисленного аргумента как беззнаковое целое число в базе 2.

Таким образом, Integer.parseInt (Integer.toBinaryString (X), 2) может генерировать исключение (со знаком или без знака).

Безопасный способ — использовать Integer.toString (X, 2); это создаст что-то менее элегантное:

Но это работает .

Я думаю, что это самый простой алгоритм (для тех, кто не хочет использовать встроенные функции):

convertNumber (1) -> «0b1»

convertNumber (5) -> «0b101»

convertNumber (117) -> «0b1110101»

Как это работает: цикл while перемещает число вправо (заменяя последний бит на второй-последний и т. Д.), Получает значение последнего бита и помещает его в StringBuilder, повторяет до тех пор, пока не останется ни одного бита (вот когда а = 0).

Источник

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Двоичная система счисления: как переводить, как реализовать на C и C#

Что такое двоичная система счисления?

Это такая бинарная система счисления (бинарная, потому что у неё имеется лишь два основания, т. е. две цифры – “0” и “1”), которая используется в самой основе компьютера, так как в компьютерных схемах, процессорах, платах имеются, так называемые, выключатели (или биты). Если на какой-либо схеме выключатель поставлен в позицию выкл., то ему соответствует цифра “0”, если вкл. – “1”. Благодаря таким вот массовым чередованиям позиций вкл\выкл и соответствующим им единиц и нулей и работают абсолютно все компьютеры.

Последовательность этих цифр, приводящая к каким-либо результатам в работе компьютера, называется машинным кодом – это самый сложный и самый низкий язык программирования, но раньше люди умудрялись программировать и на нём. Сейчас же эти коды обрамляются в более легкие и понятные ключевые слова, и формы, которые в последствии составляют различные языки программирования. Абсолютно все языки программирования в своей основе имеют под собой работу машинного кода, любая функция, любой оператор, любой метод записан в машинном коде в виде огромной последовательности единиц и нулей. Любой printf в С или Console.WriteLine обязательно разлагаются для компьютера на машинный код, только так он и может понять, что мы от него хотим.

Переводом исходного кода какого-либо языка программирования в машинный код занимается компилятор.

Алгоритм перевода в двоичную систему счисления из десятеричной.

Теперь рассмотрим алгоритм перевода каких-либо чисел из стандартной, десятеричной системы счисления в двоичную.

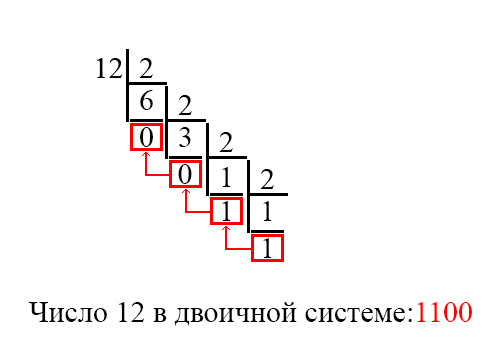
Итак, например, у нас имеется число 12 в десятеричной системе счисления, давайте переведем его в двоичную. Можно сделать это несколькими формами записи, кому как удобно.

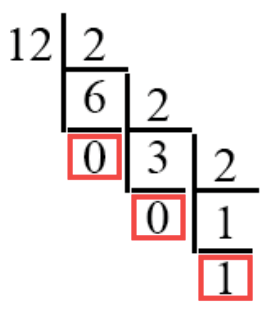
Рассмотрим первый вариант. Он будет похож на несколько видоизменённое деление в столбик, и выглядеть будет вот так:

Теперь разберём, что тут написано. Сначала мы, как и в делении в столбик, пишем число, которое мы хотим делить (12), и число, на которое делим (в двоичной системе счисления это всегда 2).

12, делённое на 2 без остатка будет равно 6. Записываем это как положено в делении в столбик.

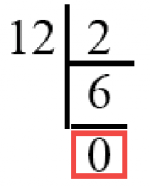
Итак, теперь стоит сказать самое главное о переводе чисел из десятичной системы счисления в двоичную: если число делится на двойку без остатка, то мы пишем ноль, если с остатком – единицу.

Рассмотрим это правило поподробнее. Мы уже сказали, что 12 / 2 =6. Остатка у нас нет. Значит мы пишем ноль. В данном методе разбора мы пишем его под цифрой 6.

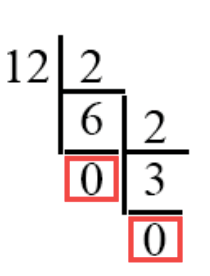
Кусочек двоичного кода мы уже получили. Вычисляем дальше.

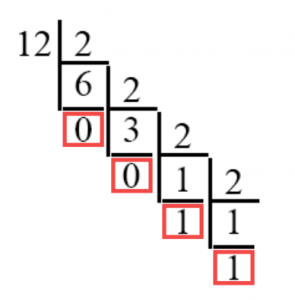
Теперь мы делим 6 на 2. Получается 3, и опять деление прошло без остатка – опять мы пишем, уже под тройкой, ноль.

Теперь делим 3 на 2. На этот раз мы понимаем, что получается ответ с остатком – 1 и 0.5. Если происходит такое, то мы откидываем полученный остаток и делим полученное число без остатка на два, при этом подписываем ниже единицу.

Далее нам стоит запомнить, что мы всегда делим последнюю единицу на два. Всегда после того или иного вычисления двоичного числа у нас так или иначе в итоге получается число 1 (как на примере, при делении 3 на 2). И абсолютно всегда мы его делим на 2. И абсолютно всегда последней цифрой в последовательности наших нулей и единиц будет цифра 1, так как все числа в двоичной системе счисления начинаются с единицы (исключение – 0, в двоичной системе счисление он и будет записан как 0).

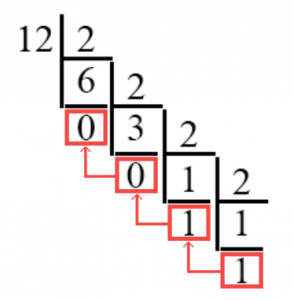
Мы поделили наше число 12, и у нас получилась последовательность: два нуля и две единицы. Однако это ещё не всё. Последний аспект, который надо запомнить – мы считываем двоичное число снизу вверх .

Поэтому мы считаем нашу последовательность “с конца”, и у нас получается число 1100. Это и есть ответ.

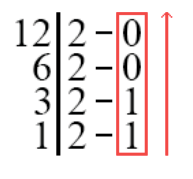
Теперь давайте рассмотрим вторую форму записи такого деления. Она менее громоздка, но по сути является той же самой формой деления.

Здесь мы просто делим получаемые числа на два через черту, и, если частное получается без остатка, через тире пишем 0, если с остатком – 1. Опять же не забываем округлять числа с остатком в меньшую сторону, делить последнюю единицу на двойку и считывать последовательность в обратном порядке.

Реализация перевода числа из десятичной системы счисления в двоичную на языке C#

Источник

Вывести на экран бинарный код целого числа

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Работа с файлами. Вывести бинарный код файла на экран в Visual C++
Доброе время суток форумчане. Нужна ваша помощь. Сразу подмечу что для кого-то ответ может.

Программа, которая выводит на экран код однобайтового целого числа
Программа, которая выводит на экран код однобайтового целого числа.

Программа, которая выводит на экран код двухбайтового целого числа
Программа, которая выводит на экран код двухбайтового целого числа.

посчитать и вывести на экран количество целого и десятичного числа
Помогите пожалуйста с заданием Посчитать и вывести на экран количество целого и десятичного числа

А вот и пример, щас попробую обяснить.

Добавлено через 5 минут 14 секунд
Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

На моё мнение так проще и удобнее. но предыдущий пример нагляднее

igor_nf, в «Философии С++» Брюса Эккеля приводится хорошая функция:

Да уж.. Действительно философ..

Ввод: 3
Вывод: 0000001

Ввод: 10
Вывод: 0000101

бред какой-то. то, что ты скидываешь, реально так выводит. смотри как у меня сделано.

есть 2 файла.
первый:

//pod.cpp неважно, что сpp расширение. раньше так стояло, сейчас менять уже не буду.

Разница есть по сравнению с пред. вариантом ?

нашла, где у тебя ошибка.
При определении функции printBinary тебе надо писать

printBinary(const unsigned char val)

printBinary(unsigned char val)

поэтому и не работает..

Добавлено через 1 минуту 2 секунды

Разница есть по сравнению с пред. вариантом ?

если вывод нужен больше пишем

вывод: 0000 0000 0000 0101

пусть будет тут а то опять искать везде кроме как тут.

Сгенерировать и вывести на экран массив из целого числа n случайных чисел
Сгенерировать и вывести на экран массив из целого числа n случайных чисел от -120 до 120. Создать.

Вывести на экран все нечетные цифры целого положительного числа
Помогите решить задачу пожалуйста» Вывести на экран все нечетные цифры целого положительного числа»

Из заданного целого числа удалить цифры 3 и 6 и вывести обратно на экран
Добрый день! Помогите ,пожалуйста, разобраться с задачей / След условие : Пользователь вводит любое.

Источник

Вывести двоичную запись числа

Помощь в написании контрольных, курсовых и дипломных работ здесь.

. Дана строка, изображающая десятичную запись целого положительного числа. Вывести строку, изображающую двоичную запись этого же числа
срочно помогите пожалуйста

Дана строка, изображающая двоичную запись целого положительного числа. Вывести строку, изображающую десятичную запись эт
Не врубаюсь вообще. Прошу использовать только библиотекu ну и стандартные тоже можно.

Дано целое число n. Вывести двоичную запись числа в обратном порядке
Дано целое число n. Вывести двоичную запись числа в обратном порядке (так проще).

Превратить двоичную запись числа в десятичную
Задан текстовый файл, каждая строка которого может рассматриваться как запись целого числа в.

Решение

Взять двоичную запись десятичного числа, посчитать количество нулей
и полученное количество вывести в двоичной системе счисления прошу помочь

Не получается сделать двоичную запись в файл
Необходимо из текстового файла взять размер массива и записать элементы массива в другой файл в.

Интерпретировать строку — двоичную запись float
Здравствуйте! Есть задача, получив на входе строку вида «10111111001010000000000000000000».

Перевод в двоичную систему счисления и запись результата в массив
Здравствуйте, как сделать перевод в двоичную систему счисления и запись результата в массив типа.

Источник

Вывод на экран двоичных чисел

Contents

Введение

Данная тема раскрывает секреты вывода на экран чисел в двоичном представлении. В ходе работы будет рассмотрено несколько новых понятий, инструкций и алгоритмов.

Циклический сдвиг и флаг переноса

Мы уже знаем, что при сложении некоторых чисел, в пятом разряде результата появляется единица, например:

Микропроцессор хранит эту единицу в специальной ячейке, называемой флагом переноса — CF (Carry Flag).

Посмотрим, как Debug отображает значение флага CF. По адресу 100h запишите инструкцию ADD AX,BX, и загрузите регистры AX = FFFFh, BX = 1h:

Жирным шрифтом выделены значения различных флагов микропроцессора. В этой строке нас интересует флаг NC (No Carry — нет переноса). Выполните трассировку инструкции, и вновь просмотрите регистры.

Состояние флага изменилось CY (Carry — перенос). В результате сложения чисел произошел перенос единицы в пятый разряд, при этом CF принял значение CY.

Если операция проходит без переноса в пятый разряд, то флаг переноса принимает значение NC. Например, выполните сложение 2 + 3, и убедитесь, что CF = NC.

Для вывода на экран двоичных чисел, мы используем инструкцию RCL (Rotate Carry Left), которая сдвигает число на один бит влево через флаг переноса.

В исходном состоянии BL = B7h (10110111b). На рисунке показано состояние регистра BL и флага CF после сдвига числа на один бит влево:

CF	BL
0	10110111	B7h
1	01101110	6Eh
0	11011101	DDh
1	10111010	BAh
1	01110101	75h
0	11101011	EBh
1	11010110	D6h
1	10101101	ADh
1	01011011	5Bh
0	10110111	B7h

После прохождения флага переноса, бит возвращается в младший разряд регистра BL. Через девять циклических сдвигов число полностью вернется в регистр BL:

1. Загрузите в регистр BL число B7h
2. По адресу 100h запишите инструкцию RCL BL,1
3. Проверьте стартовый адрес IP = 100h
4. Выполните инструкцию 9 раз (возвращая IP = 100h)
5. Убедитесь, что число прошло все стадии сдвига, и вернулось в исходное состояние.

Инструкцию RCL можно использовать и с другими регистрами. Например:
RCL DL,1 будет сдвигать байт в регистре DL на один бит влево, через флаг переноса.

Далее мы научимся преобразовывать значение флага переноса, в символ «1» или «0» для последующей печати.

Сложение с использованием флага переноса

Для вывода символа на экран мы использовали функцию 02h прерывания INT 21h. При этом, в регистре DL мы указывали ASCII код символа. Вывод на экран двоичного числа сводится к последовательной печати символов «0» и «1». Эти символы имеют коды: «0» — 30h, «1» — 31h

При циклическом сдвиге RCL все биты числа (от старшего до младшего) проходят через флаг переноса. Выполняя сложение CF + 30h мы получим код символа «0» или «1» (в зависимости от значения CF):

Инструкция ADC (Add with Carry) выполняет сложение двух чисел, и добавляет к сумме бит CF. Например, для суммы DL + 30h + CF, мнемокод инструкции выглядит так:

Результат сложения попадает в регистр DL. Если до выполнения инструкции регистр DL = 0, то после суммирования в DL появится код символа «0» или «1» (30h или 31h).

Обобщив все идеи, мы получаем алгоритм вывода на экран старшего бита числа:

1. сдвигаем число влево на один бит;
2. преобразуем флаг переноса в код символа;
3. выводим символ на экран.

Если этот алгоритм повторить 8 раз (для байта) или 16 раз (для слова), то на экране появится цепочка нулей и единиц, соответствующая двоичному представлению заданного числа.

Организация цикла

Рассмотрим программу вывода на экран старшего бита числа B7h:

Перед сложением необходимо обнулять DL, иначе код символа будет сформирован неверно. После RCL сдвига, бит попадает в CF и добавляется в сумму:

В результате сложения, регистр DL получает код символа «1» или «0».

Для вывода остальных битов числа B7h, надо повторить выделенный фрагмент еще семь раз. Организацию циклических повторов мы доверим инструкции LOOP:

Инструкция LOOP работает в паре с регистром CX, и выполняет три действия:

1. проверяет число в регистре CX;
2. если CX > 0, то LOOP уменьшает CX на 1 и возвращает управление на 107 адрес;
3. если CX = 0, то LOOP передает управление следующей инструкции (INT 20h).

Почему в качестве счетчика повторений выбран регистр CX? Буква «C» в названии регистра CX указывает на его функцию: Count (счетчик). Поэтому CX в основном используется при организации циклов.

Введите программу в память. Проверьте IP и выполните команду «G»:

Испытайте программу с другим числом, для этого измените значение регистра BH:

Число FEh можно записать иначе:

Проверьте действие программы со следующими числами:

Самостоятельно переведите эти числа из шестнадцатеричной формы в двоичную, и сравните свои результаты с результатами программы.

Основная задача Debug — это пошаговая отладка программ. Поэтому, в качестве следующего упражнения выполните трассировку программы, анализируя:

• содержимое регистров BH, DL, CX;
• состояние флага переноса CF;
• текущую мнемоническую инструкцию.

Для выполнения прерываний (INT 21h, INT 20h) используйте команду «P» (Proceed — переход). В отличие от команды «G», в команде «P» не надо указывать адрес остановки.

1. Измените программу так, чтобы она добавляла символ «b» в конец двоичной записи.
2. Напишите программу для вывода на экран двоичного слова из регистра BX.

Источник