Вывести число пи с точностью до сотых java

MnogoBlog

как создать сайт на wordpress, настроить и оптимизировать wordpress

Java Урок 15: Класс Math (основные математические функции)

Для решения задач нередко требуется использование математических функций. В Java такие функции включены в класс Math.
Рассмотрим: Math sqrt, cbrt, округления, тригонометрия, радианы, min, max, модуль числа, PI
Скачать исходники для статьи можно ниже
Фреш казино зеркало

Извлечение квадратного корня.

Вывод программы:
Корень квадратный 4 = 2.0

Извлечение кубического корня.

Вывод программы:
Кубический корень 8 = 2.0

Округления.

Вывод программы:
Округление 1.4 = 1.0
Округление вверх 1.4 = 2.0
Округление вниз 1.4 = 1.0

Тригинометрические функции.

Вывод программы:
sin 0.5 = 0.479425538604203
cos 0.5 = 0.8775825618903728
tan 0.5 = 0.5463024898437905
asin 0.5 = 0.5235987755982989
acos 0.5 = 1.0471975511965979
atan 0.5 = 0.4636476090008061

Перевод градусов в радианы.

Вывод программы:
1.0 радиан = 57.29577951308232 градусов
180.0 градусов = 3.141592653589793 радиан

Минимальное число.

Вывод программы:
Минимальное число:2

Максимальное число.

Вывод программы:
Максимальное число:5

Абсолютное число.

Вывод программы:
модуль числа -5 = 5

Число Пи.

Вывод программы:
3.141592653589793

Нахождение гипотенузы.

Вывод программы:
Гипотенуза = 5.0

Похожие записи:

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

«Краник», или алгоритм для поиска цифр числа Пи

Привет, Хабр! Недавно столкнулся с задачей подсчёта числа Пи до знака, номер которого будет выбирать пользователь. Сразу полез на Википедию, почитать, что за зверь такой, это Пи, и как его находить с заданной точностью. Формул, описывающих число Пи, уйма. Но для решения моей задачи всё в этих формулах упирается либо в точность и длину базовых типов языка (я выбрал Java), либо (для решения предыдущей проблемы) в длинную арифметику, которую мне реализовывать не очень-то хотелось. Хотелось найти какой-то алгоритм, позволяющий найти число Пи вплоть до заданного знака, причём ровно до этого знака, а не находить длиннющее число, а потом обрезать его, чтобы отдать пользователю то, что он просил.

И я нашёл такой алгоритм, тот самый алгоритм «краника». Слово краник звучит здесь странно, но я не нашёл лучшего способа перевести название этого алгоритма с английского, как перевести дословно. Вообще, в оригинале это звучит как «A Spigot Algorithm for the Digits of Pi». Авторами алгоритма и его нарицателями являются американские математики Стенли Рабинович (Stanley Rabinowitz) и Стен Вэгон (Stan Wagon). Создали свой алгоритм для нахождения цифр числа Пи эти два товарища в 1995 году. Сама же идея алгоритма вышла из-под пера некого Сейла (Sale) ещё в 1968 году, и предназначался тот алгоритм для нахождения цифр числа e.

Вообще, англо-русские словари дают перевод слова spigot как “втулка”. Этот перевод ясности не даёт никакой. Поэтому я перевёл это слово как «краник», так как spigot в английском языке описывается как механизм, регулирующий поток жидкости. Идея же алгоритма в том и заключается, что за одну итерацию мы получаем ровно одну цифру числа Пи и потом её не используем. То есть цифры как бы вытекают из алгоритма, как вода из крана.

Теперь сам алгоритм. Я не буду вдоваться во всю математику (чего я, собственно, и не делал, разбирая алгоритм), подробнее о нём вы можете почитать здесь. К слову, по этой ссылке, есть и реализация алгоритма для поиска 1000 цифр числа Пи на Паскале, которой я по своей лени и решил сразу же воспользоваться. Переписал на Java, ан нет — не заработало. Выводило какую-то непонятную мне белиберду. Я это дело и бросил, так как отлаживать код, которого не понимаешь, сами знаете, как тушить горящее масло водой. Поэтому решил-таки разобраться с алгоритмом самолично.
Для нахождения n знаков числа Пи, понадобится массив длиной [10 * n / 3]. Причём целых чисел. Особенность алгоритма в том, что используется только целочисленная арифметика. Инициализируем все ячейки массива числом 2.

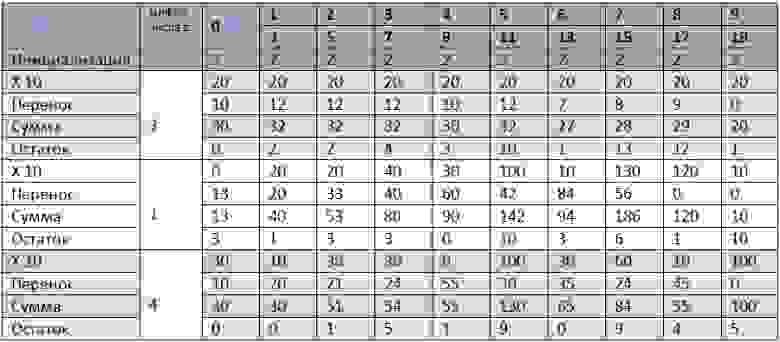
Далее, чтобы найти одну цифру числа Пи, необходимо пройтись по всем ячейкам массива с конца к началу и выполнить несложные действия. На примере таблицы, рассмотрим всё по порядку. Допустим, мы хотим найти 3 цифры числа Пи. Для этого нам необходимо зарезервировать 3 * 10 / 3 = 10 ячеек целого типа. Заполняем их все числом 2. Теперь приступим к поиску первой цифры…

Начинаем с конца массива. Берём последний элемент (под номером 9, если начинать счёт с 0. Этот же номер будем называть числителем, а тот, что под ним в таблицу – знаменателем) — он равен 2. Умножаем его на 10 (2 * 10 = 20). К получившемуся числу 20 прибавляем число из ячейки «Перенос» – число, которое переносится из более правой операции. Разумеется, правее мы ничего не считали, поэтому это число равно 0. Результат записываем в «сумму». В «остаток» записываем остаток от деления суммы на знаменатель: 20 mod 19 = 1. А сейчас считаем «перенос» для следующего шага. Он будет равен результату деления суммы на знаменатель, умноженному на числитель: (20 / 19) * 9 = 9. И записываем полученное число в ячейку с «переносом», стоящую левее от текущего столбца. Проделываем те же действия с каждым элементом массива (умножить на 10, посчитать сумму, остаток и перенос на следующий шаг), пока не дойдём до элемента с номером 0. Здесь действия немного отличаются. Итак, посмотрим, что у нас в таблице. Под нулём – элемент массива, равный 2, и перенос из предыдущего шага, равный 10. Как и в предыдущих шагах, умножаем элемент массива на 10 и прибавляем к нему перенос. В сумме получили 30. А сейчас делим сумму не на знаменатель, а на 10 (!). В итоге получаем 30 / 10 = 3 + 0 (где 0 – остаток). Полученное число 3 и будет той заветной первой цифрой числа Пи. А остаток 0 записываем в отведённую ему ячейку. Для чего были остатки? Их нужно использовать в следующей итерации – чтобы найти следующую цифру числа Пи. Поэтому разумно сохранять остатки в наш изначальный массив размером 10 * n / 3. Таким образом, видно, что возможности алгоритма упираются именно в размер этого массива. Поэтому число найденных цифр ограничивается доступной памятью компьютера либо языком, на котором вы реализуете алгоритм (конечно, языковые ограничения можно обойти).

Но это не всё. Есть один нюанс. В конце каждой итерации может возникать ситуация переполнения. Т.е. в нулевом столбце в «сумме» мы получим число, большее, чем 100 (эта ситуация возникает довольно редко). Тогда следующей цифрой Пи получается 10. Странно, да? Ведь цифр в десятичной системе счисления всего от 0 до 9. В этом случае вместо 10 нужно писать 0, а предыдущую цифру увеличивать на 1 (и стоящую перед последней, если последняя равна 9, и т.д.). Таким образом, появление одной десятки, может изменить одну и больше найденных ранее цифр. Как отслеживать такие ситуации? Необходимо найденную новую цифру первоначально считать недействительной. Для этого достаточно завести одну переменную, которая будет считать количество недействительных цифр. Нашли одну цифру – увеличили количество недействительных цифр на 1. Если следующая найденная цифра не равна ни 9, ни 10, то начинаем считать найденные ранее цифры (и помеченные как недействительные) действительными, т.е. сбрасываем количество недействительных цифр в 0, а найденную новую цифру начинаем считать недействительной (т.е. можно сразу сбрасывать в 1). Если следующая найденная цифра равна 9, то увеличиваем количество недействительных цифр на 1. Если же следующая цифра 10, то увеличиваем все недействительные цифры на 1, вместо 10 записываем 0 и этот 0 считаем недействительным. Если эти ситуации не отслеживать, то будут появляться единичные неверные цифры (или больше).

Вот и весь алгоритм, который авторы сравнили с краном. Ниже привожу код метода, реализованного на Java, который возвращает строку с числом Пи.

Ради интереса провёл тест производительности алгоритма в зависимосты от величины n (количество цифр, которые нужно найти). Получился вот такой график:

Для нахождения миллиона цифр понадобилось больше восьми с половиной часов. Тесты я проводил без печати результатов и использовал не StringBuilder, а байтовый массив.

Итак, подытожим. Главными достоинствами алгоритма являются его простота (посчитать можно без проблем и руками), а также использование только целочисленной арифметики, что ускоряет процесс вычислений и добавляет точности. Главным же недостатком я считаю ограниченность алгоритма (памятью).

P. S.: Алгоритм на основе формулы Bailey–Borwein–Plouffe из разряда «краниковых» ранее обсуждался на Хабре в этой статье.

Источник

PI in Java – Math.PI Java Example

To get and use the PI (π) value in Java Language, we can use Math.PI constant defined in the java.lang.Math class. The Math.PI is a static final double type variable having a double value that is closer than any other to π, the ratio of the circumference of a circle to its diameter.

public static final double PI = 3.14159265358979323846;

Since it is a static variable so, we can directly access it through its class name like Math.PI. Example:-

If we import Math class statically and then we can access PI without calling through its class name.

The “import static java.lang.Math.*;” statement will import all static members of the Math class. But if we want to import only the PI variable of the Math class, not other static methods and variables of the Math class then we can use the “import static java.lang.Math.PI;” statement.

How to Use PI in Java

To use PI in Java, first get the PI value by calling PI variable of Math class, and then use it in the program. Let us see this through an example:-

Java Program to Find the Area of a Circle using Math.PI

In this example, we are accessing the PI value through the class name directly. Using import statement we can get the PI value without using its class name.

In this example, even though we need only PI value but we are importing all the static methods and variables of the Math class which are not being used in this program. Therefore it is better to import only the PI variable of the Math class to get the π value.

If we import the PI variable of the Math class through static import then only the PI variable will be available to the class, other static methods and variables will not be there.

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or you find anything incorrect? Let us know in the comments. Thank you!

Источник

Java вычислить число Пи до 6 значащих цифр

У меня проблемы с этой программой, мы должны вычислить число Пи до шести значащих цифр, БЕЗ ОКРУГЛЕНИЯ и БЕЗ использования константы математической библиотеки, программа также должна показывать количество итераций, которые потребовались для достижения точности 6 знаков, а также математическая константа в выходных данных, пока я просто пытаюсь осмыслить вычисление числа пи, я совершенно не понимаю, как получить шесть 6 фиг с округлением или без него, не говоря уже о том, как определить, сколько итераций потребовалось для достичь 6 сиг, фиг, пожалуйста, помогите.

«Напишите алгоритм и программу для вычисления π, используя формулу, описанную в тексте PI/4 =1-(1/3)+(1/5)-(1/7)+(1/9). ». Вывод будет включать ваше вычисленное значение для π, ожидаемое значение константы математической библиотеки для π и количество итераций, которые потребовались для достижения шести -существенная цифровая точность. Количество итераций может превышать 250 000. Сделайте вывод чистым и легким для чтения для сравнения результатов.

Это код, который у меня есть до сих пор для вычисления числа Пи, но даже он, я не уверен, правильный.

3 ответа

вывод

Таким образом, по-видимому, существует способ сделать априорную оценку ошибки с помощью теоремы о переменных рядах. Но предположим, что вы не знаете теорему или не доверяете своей математике (если вы знаете, просто измените 100.0 выше на правильное число. 800000.0, как указано выше, будет работать, только с трудом). Возможно, здесь есть что-то более безопасное, хотя было бы лучше проверять точность оценки только каждые 1000 раз в цикле, а не каждый раз?

В идеале вы должны инкапсулировать свои вычисления в классе:

Тогда цикл становится довольно тривиальным:

Источник

Вывести число пи с точностью до сотых java

В уроке 8 мы затронули логические операторы, они нам были необходимы для формирования логического выражения в условиях if. Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.

Но для начала, выясним, что же такое операторы. Операторы это специальные символы, отвечающие за ту или иную операцию, например сложение, умножение, сравнение. Все операторы в Java можно разбить на 4 класса — арифметические, битовые, операторы сравнения и логические.

Арифметические операторы в Java

Для стандартных арифметических операций, таких как сложение, вычитание, умножение, деление в Java используются традиционные символы, к которым мы привыкли со школы:

Примечание: при операции деления, если оба аргумента являются целыми числами, то в результате получим целое число. Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа .0 или .d. Пример:

В Java также имеется специальный оператор %, обозначающий остаток от делния.

Пример использования: дан массив целых чисел, вывести на консоль только те числа, которые делятся на 3.

Операции с присваиванием

Рассмотрим задачу вывода на экран 10 первых четных чисел чисел

мы можем записать сокращенно

+= это оператор сложения с присваиванием. Подобные операторы есть для всех основных 5 операций, рассмотренных выше

Пример использования: Найти факториал числа 7.

Инкрементирование и декрементирование

Инкремент, обозначается ++ и увеличивает значение переменной на единицу. Декремент обозначается — и уменьшает значение на единицу. С инкрементом и декрементом мы часто встречаемся в цикле for.

Инкремент и декремент бывают двух форм

Различие префиксной и постфиксной формы проявляется только тогда, когда эти операции присутствуют в выражениях. Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример

В первом случае сначала переменная a увеличится на 1, потом произойдет вычисление всего выражения. Во втором случае произойдет вычисление выражения при старом значении b = 3, и после вычисления b увеличится на 1, на результат в postfix это уже не повлияет.

Если вы поняли принцип работы постфиксного и префиксного инкремента/декремента, то предлагаю решить в уме такую задачу:

Вопрос: чему в итоге равны x и y? После того, как вы сделали предположение, проверьте его в java.

Задача со зведочкой. Дан код:

Какие числа будут выведены на экран? Почему? Разобраться самостоятельно.

Примечание: инкремент и декремент применяются только к переменной. Выражение вида 7++ считается недопустимым.

Математические функции и константы (класс Math)

Для решения задач нередко требуется использование математических функций. В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.

Источник