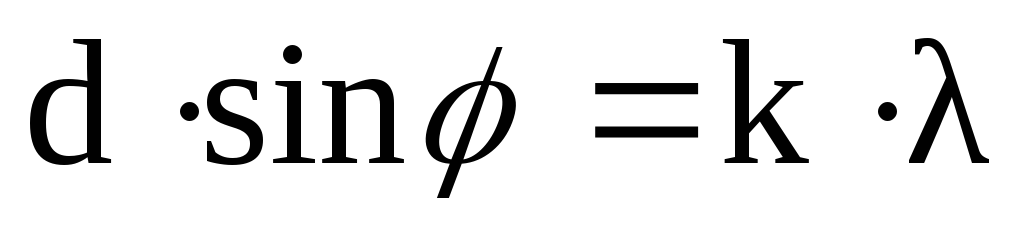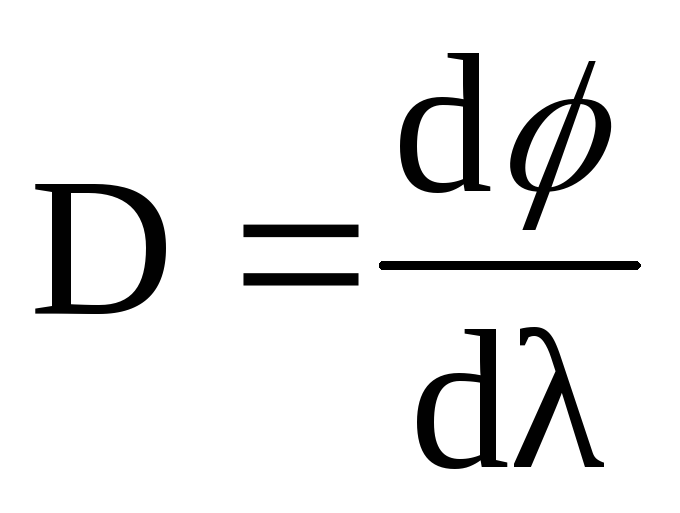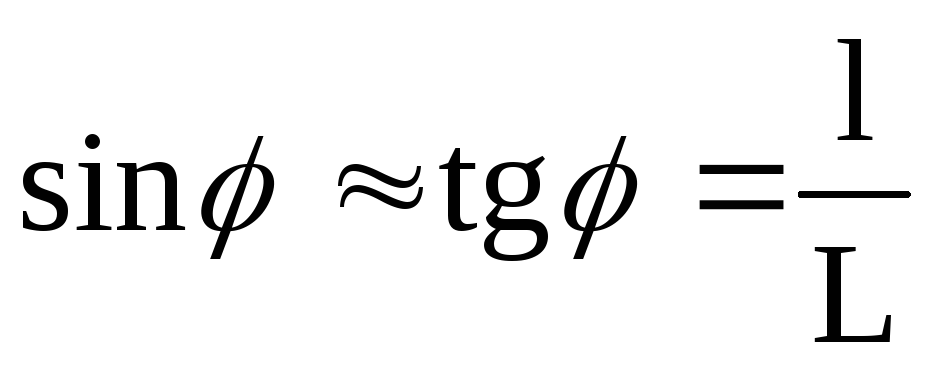Лабораторная работа 4.3 определение постоянной дифракционной решетки
1. Цель работы:
С помощью измерений и последующего использования формулы для главных максимумов дифракционной решетки определить постоянную дифракционной решетки и оценить допущенную погрешность.
2. Теоретическая часть
Такие простейшие оптические явления, как прямолинейность распространения в однородной среде, отражение и преломление света можно объяснить с помощью как корпускулярных, так и волновых представлений о природе света. И те, и другие содержат ряд парадоксов. Однако понять и объяснить такие явления, как интерференция, дифракция и поляризация света можно только в том случае, если считать, что свет — волна. Х. Гюйгенс сформулировал принцип, согласно которому каждая точка оптической среды, которой в данный момент времени достигла световая волна, представляет собой элементарный источник сферических световых волн, а волновой фронт в любой следующий момент времени представляет собой огибающую (результат сложения) волн от элементарных источников.
В этом случае малое препятствие на пути волнового фронта не приведет к возникновению геометрической тени, поскольку свет от элементарных источников, расположенных на волновом фронте в стороне от препятствия, будет попадать в область тени. Эффективно это выглядит как огибание светом препятствия. Такое явление называется дифракцией.
Э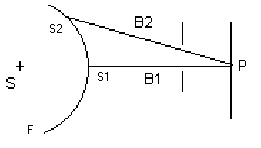 
лементарные источники на одном и том же сферическом фронте F когерентны. Если они расположены на разных расстояниях от выбранной точки наблюдения Р (рис.1), то в общем случае свет от них будет приходить в эту точку в разных фазах. Результат сложения когерентных волн будет
определяется разностью их фаз.
Если расстояния В1 (кратчайшее расстояние от фронта волны, испускаемой источником S, до точки наблюдения Р) и В2 различаются на половину длины волны света, то колебания от соответствующих элементарных источников S1 и S2 приходят в точку Р в противофазе и гасят друг друга. То же самое происходит, если эти расстояния различаются на любое нечетное число полуволн. Если же разность расстояний равна длине волны излучения или кратна ей, то волны от двух источников приходят в точку Р в одинаковых фазах и усиливают друг друга при сложении.
Сферический волновой фронт может быть разбит на зоны Френеля, которые представляют собой такие кольцевые области, что свет от любой пары соседних зон будет приходить в точку наблюдения в противофазе. Это возможно тогда, когда расстояние от краев соседних зон до точки наблюдения будут отличаться друг от друга на половину длины волны. Если между источником и экраном имеется преграда в виде отверстия, то суммарная освещенность в точке Р будет зависеть от того, четное или нечетное число зон Френеля соответствуют волновому фронту, достигшему этого отверстия. В первом случае произойдет практически полное гашение света, во втором случае останется нескомпенсированный вклад одной из зон.
Если вырезать специальную преграду в виде концентрических колец, перекрывающих путь свету только от четных или только от нечетных зон Френеля для данного взаимного расположения источника, преграды и экрана, то компенсации света от соседних зон, как это имеет место, когда никакой преграды нет, происходить не будет. Поэтому будет иметь место усиление освещенности в данной точке экрана.
Эти соображения позволяют установить, где будут находиться минимумы засветки экрана при дифракции плоскопараллельного пучка света на щели. После прохождения щели свет попадает на экран под разными углами φ к первоначальному направлению. Если ширина b щели (рис. 2) такова, что в направлении φ на ней укладывается четное число зон Френеля, то в данном направлении произойдет взаимное гашение света, и на экране будет минимум засветки. Для того чтобы узнать, сколько зон Френеля укладывается на щели, необходимо определить разность хода двух лучей, проходящих через границы щели.
Если окажется, что разность хода равна четному числу полуволн, то и зон Френеля будет четное число, что соответствует минимуму засветки экрана в данном направлении. Из рисунка видно, что упомянутая разность хода равна bsin. Поэтому условие минимума освещенности на щели имеет вид
, (1)
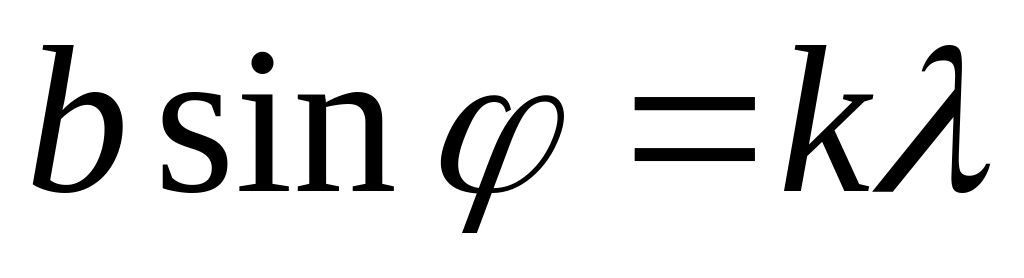
где k — целые числа 1, 2, 3… .
Дифракционной решеткой называется система параллельных щелей, ширина которых и промежутки между которыми сравнимы с длиной волны падающего света. Расстояние d, равное сумме ширины b щели и промежутка a между щелями, называется постоянной решетки (или периодом решетки, или шагом решетки), d = a + b. При дифракции света на дифракционной решетке максимумы засветки для различных длин волн оказываются в разных местах экрана, белый свет разлагается в спектр. Каждое вещество обладает своими спектральными характеристиками, поэтому дифракционную решетку можно использовать для спектрального анализа.
Условие, определяющее положение максимумов или минимумов засветки экрана при дифракции на решетке, нельзя записать так же просто, как соответствующее условие для щели, поскольку эта преграда устроена более сложным образом. Формула, описывающая положение главных максимумов дифракционной решетки, имеет вид
, (2)
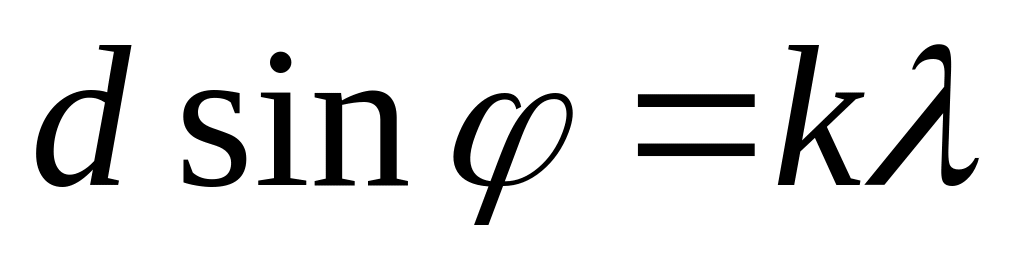
где d — постоянная решетки, — угол между нормалью к решетке и направлением на точку, в которой имеется максимум засветки,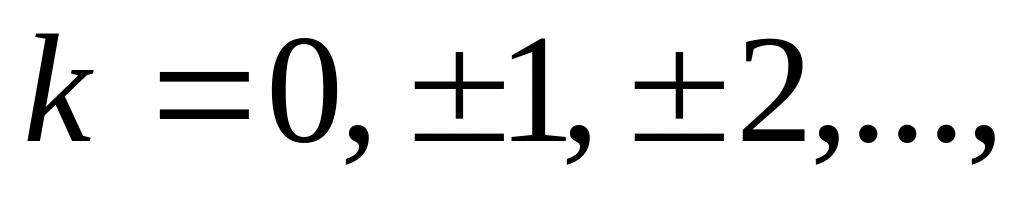 
— длина волны падающего света.
В некоторых случаях может оказаться, что не все главные максимумы из тех, что описываются формулой, видны. Это происходит в тех случаях, когда ширина щели в целое число раз отличается от расстояния между щелями. В общем же случае можно точно указать, какое количество К главных максимумов можно наблюдать при заданных условиях. Полагая sin = 1, что соответствует максимальному значению левой части формулы, а, значит, и максимальному значению номера k в правой части, получим
. (3)
Однако величина в правой части получившегося соотношения не всегда является целой, в то время как число максимумов — целое число. Поэтому следует взять целую часть (не округлить!) получившегося выражения. Учитывая, что и с другой стороны от нулевого главного максимума имеется столько же главных максимумов, а также включая в общее их число нулевой главный максимум, получим
. (4)
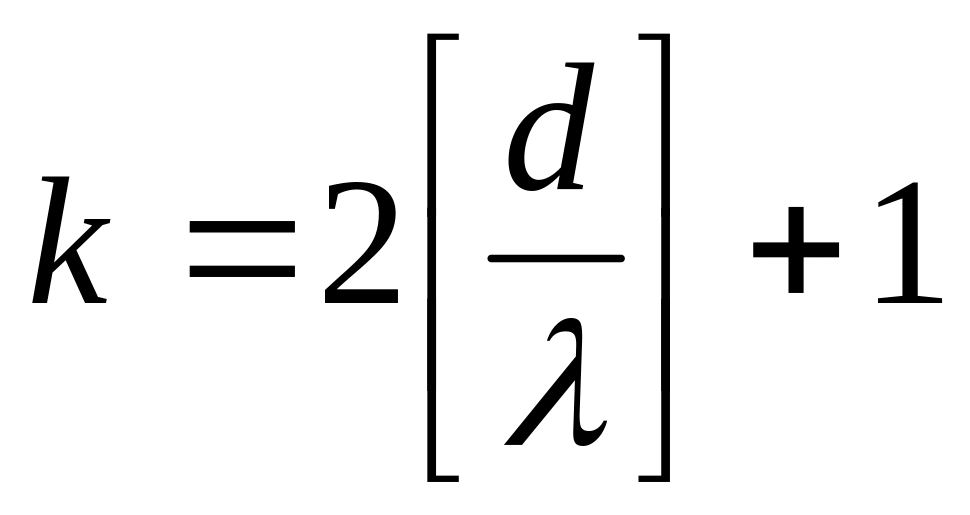
При исследовании спектров веществ с помощью дифракционной решетки важное значение имеет ее разрешающая способность, т. е. возможность наблюдать две близкие линии спектра раздельно. Эта величина характеризуется отношением малой разности длин волн этих линий к длине волны любой из них и равна 
. Можно показать, что разрешающая способность равна
, (5)
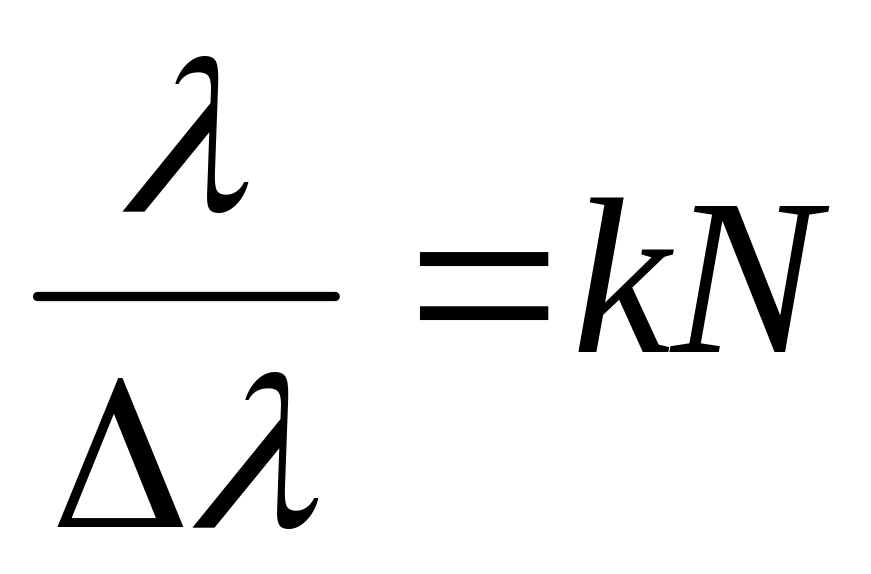
где k — номер главного максимума, в котором проводится измерение, N — полное число линий решетки, на которые падает излучение. Увеличение обоих последних параметров повышает разрешающую способность решетки.
В современной физике (и в данной учебной лабораторной работе) большую роль играет лазерный источник света. Принцип работы лазера состоит в том, что из двух известных механизмов излучения света атомом — спонтанного и вынужденного — специально используется последний. При спонтанном излучении возбужденный тем или иным способом атом испускает фотон в произвольном направлении, с произвольными поляризацией и фазой. При вынужденном излучении возбужденный атом испускает фотон под воздействием еще одного фотона, принадлежащего полю излучения, в котором находится атом. В последнем случае излучаемый фотон имеет те же импульс, поляризацию и фазу, что и тот, который стимулировал его излучение. Поскольку вместо одного налетевшего фотона теперь появляется два, происходит усиление излучения, которое является когерентным.
Источник
Вывод формулы дифракционной решетки
Дифракционная решетка – оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равностоящих друг от друга щелей. Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места – щели – будут пропускать свет, штрихи – рассеивать и не пропускать (рис. 3).
Рис. 3. Сечение дифракционной решетки (а) и ее графическое изображение (б)
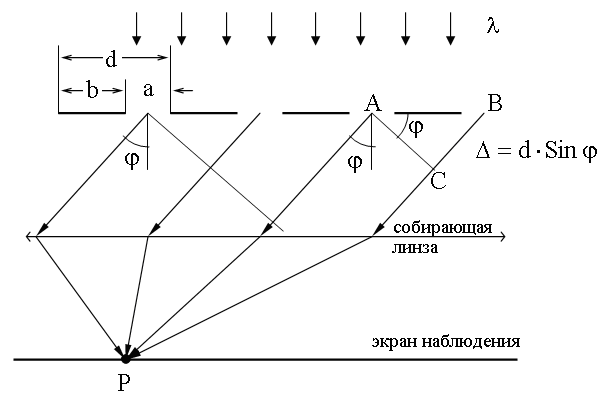
Для вывода формулы рассмотрим дифракционную решетку при условии перпендикулярного падения света (рис. 4). Выберем два параллельных луча, прошедших две щели и направленных под углом φ к нормали.
С помощью собирающей линзы (глаза) эти два луча попадут в одну точку фокальной плоскости Р и результат их интерференции будет зависеть от разности фаз или от их разности хода. Если линза стоит перпендикулярно лучам, то разность хода будет определяться отрезком ВС, где АС – перпендикуляр к лучам А и В. В треугольнике АВС имеем: АВ = а + b = d – период решетки, ВАС = φ, как углы с взаимно перпендикулярными сторонами.
Лучи А и В дадут интерференционный максимум, если выполнится условие (4), т.е.
Из формул (8) и (9) получим формулу дифракционной решетки:
Рис. 4. Дифракция света на дифракционной решетке
Т.е. положение световой линии в дифракционном спектре не зависит от вещества решетки, а определяется периодом решетки, который равен сумме ширины щели и промежутка между щелями.
Разрешающая способность дифракционной решетки.
Если свет, падающий на дифракционную решетку полихроматический, т.е. состоит из нескольких длин волн, то в спектре максимумы отдельных будут под разными углами. Характеризовать разрешение можно угловой дисперсией:
где d – угловое расстояние между двумя линиями спектра, которые имеют разность длин волн равную d.
При дифференцировании формулы дифракционной решетки получим, что дисперсия равна:
Следовательно, угловая дисперсия тем больше, чем больше порядок спектра k.
II. Работа студентов во время практического занятия.
Получить допуск к занятию. Для этого необходимо:
– иметь конспект в рабочей тетради, содержащий название работы, основные теоретические понятия изучаемой темы, задачи эксперимента, таблицу по образцу для внесения экспериментальных результатов;
– успешно пройти контроль по методике проведения эксперимента;
– получить у преподавателя разрешение выполнять экспериментальную часть работы.
Выполнение лабораторной работы, обсуждение полученных результатов, оформление конспекта.
Приборы и принадлежности
Рис. 5 Схема установки
1. Дифракционная решетка.
2. Источник света.
В данной лабораторной работе предлагается определить длины волн для красного и зеленого цветов, которые получаются при прохождении света через дифракционную решетку. При этом на экране наблюдается дифракционный спектр. Дифракционная решетка состоит из большого числа параллельных щелей, очень малых по сравнению с длиной волны. Щели позволяют проходить свету, в то время как пространство между щелями непрозрачно. Общее количество щелей – N, с расстоянием между их центрами – d. Формула дифракционной решетки:
где d – период решетки; sin φ – синус угла отклонения от прямолинейного распространения света; k – порядок максимума; λ – длина волны света.
Экспериментальная установка состоит из дифракционной решетки, источника света и подвижного экрана с линейкой. На экране наблюдается дифракционный спектр (рис. 5).
Расстояние от дифракционной решетки до экрана L может изменяться перемещением экрана. Расстояние от центрального луча света до отдельной линии спектра l. При малых углах φ:
Тогда из формулы дифракционной решетки получим:
, следовательно 
Источник
5.5. Дифракционная решетка
Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.
Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)
Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).
Рис. 5.6. Дифракция от двух щелей
Период дифракционной решетки — это расстояние между серединами соседних щелей:
Разность хода двух крайних лучей равна
Если разность хода равна нечетному числу полуволн
то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид
Эти минимумы называются дополнительными.
Если разность хода равна четному числу полуволн
то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид
Это формула для главных максимумов дифракционной решетки.
Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:
Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид
Здесь k’ может принимать все целочисленные значения, кроме 0, N, 2N, . . Следовательно, в случае N щелей между двумя главными максимумами располагается (N–1) дополнительных минимумов, разделенных вторичными максимумами, создающими относительно слабый фон.
Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.
Важной характеристикой всякого спектрального прибора является разрешающая способность.
Разрешающая способность спектрального прибора — это безразмерная величина
Источник
