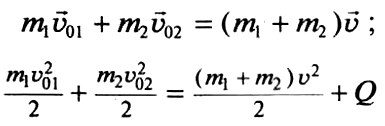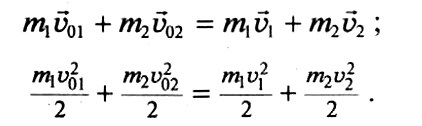Вывести формулу закона сохранения энергии

Раздел ОГЭ по физике: 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения.

1. Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.

Энергией называют физическую величину, которая характеризует способность тела или системы взаимодействующих тел совершить работу.
Единица энергии в СИ 1 Джоуль (Дж).

2. Кинетической энергией называется энеpгия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энеpгия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела.

Кинетическая энергия Е_к тела массой m, движущегося со скоростью v, определяется по формуле Е_к =mv 2 /2

3. Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.

Потенциальной энергией обладают, например, груз, поднятый над поверхностью Земли, и сжатая пружина.
Потенциальная энергия поднятого груза Е_п = mgh .
Кинетическая энергия может превращаться в потенциальную, и обратно.

4. Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энеpгия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.

Механическая энергия характеризует способность тела или системы тел совершить работу вследствие изменения скорости тела или взаимного положения взаимодействующих тел.

5. Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энеpгия не зависит от механической энергии тела и зависит от строения тела и его состояния.

6. Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.

Закон сохранения механической энергии: если между телами системы действуют только силы тяготения и силы упругости, то сумма кинетической и потенциальной энергии остается неизменной, то есть механическая энергия сохраняется.

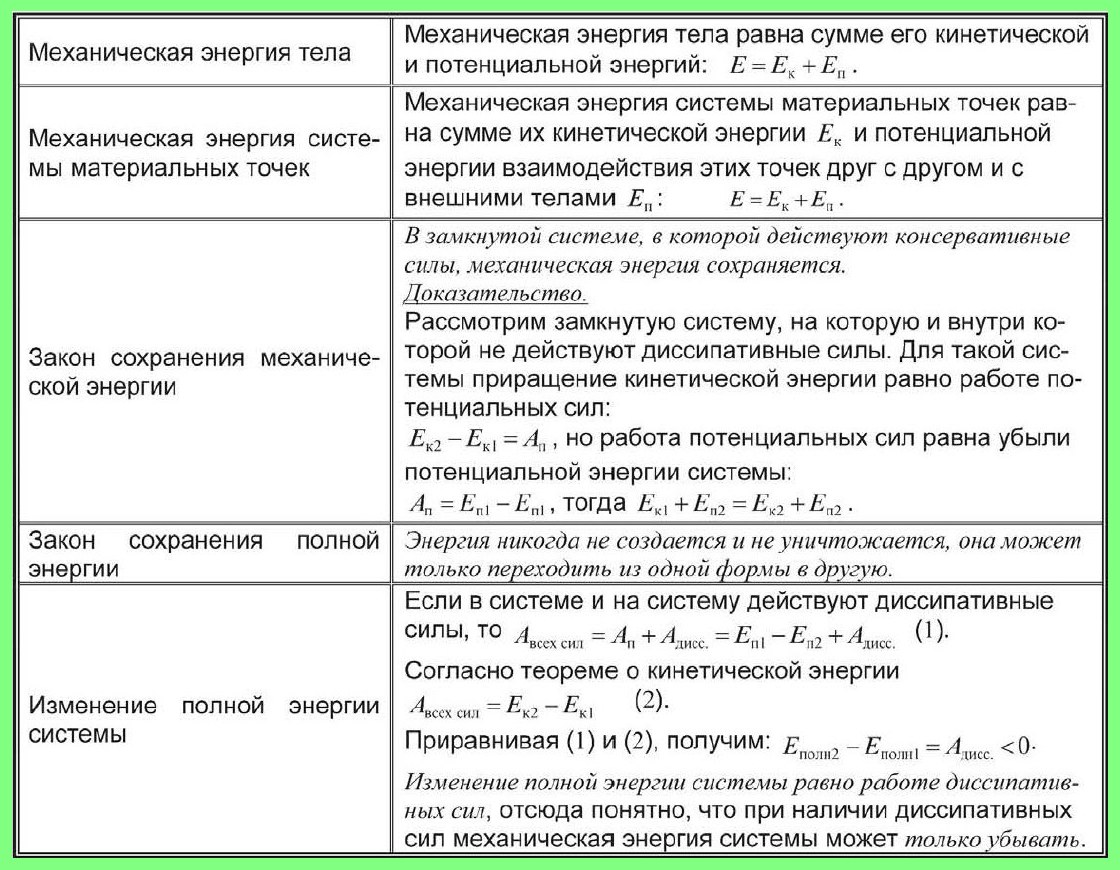
Таблица «Механическая энергия. Закон сохранения энергии».

7. Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = А_внешн + А_диссип

Если система тел замкнута (А_внешн = 0), то ΔW = А_диссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения).

Если система тел консервативна (то есть отсутствуют силы трения и сопротивления А_тр = 0), то ΔW = А_внешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил.

8. Закон сохранения механической энергии: В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔW = 0 или W_п1 + W_к1 = W_п2 + W_к2 . Применим законы сохранения импульса и энергии к основным моделям столкновений тел.

Абсолютно неупругий удар (удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью). Импульс системы тел сохраняется, а полная механическая энергия не сохраняется:

Абсолютно упругий удар (удар, при котором сохраняется механическая энергия системы). Сохраняются и импульс системы тел, и полная механическая энергия:

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

Схема «Механическая энергия.
Закон сохранения энергии. Углубленный уровень«

Конспект урока по физике «Механическая энергия. Закон сохранения энергии». Выберите дальнейшие действия:

Источник

§ 22. Вывод закона сохранения механической энергии

Из курса физики 8 класса вы знаете, что сумма потенциальной (mgh) и кинетической (mv 2 /2) энергии тела или системы тел называется полной механической (или механической) энергией.

Вам известен также закон сохранения механической энергии:

механическая энергия замкнутой системы тел остаётся постоянной, если между телами системы действуют только силы тяготения и силы упругости и отсутствуют силы трения

Потенциальная и кинетическая энергия системы могут меняться, преобразуясь друг в друга. При уменьшении энергии одного вида на столько же увеличивается энергия другого вида, благодаря чему их сумма остаётся неизменной.

Подтвердим справедливость закона сохранения энергии теоретическим выводом. Для этого рассмотрим такой пример. Маленький стальной шарик массой m свободно падает на землю с некоторой высоты. На высоте h₁ (рис. 51) шарик имеет скорость v₁, а при снижении до высоты h₂ его скорость возрастает до значения v₂.

Рис. 51. Свободное падение шарика на землю с некоторой высоты

Работа действующей на шарик силы тяжести может быть выражена и через уменьшение потенциальной энергии гравитационного взаимодействия шарика с Землёй (Е_п), и через увеличение кинетической энергии шарика (Е_к):

Поскольку левые части уравнений равны, то равны и их правые части:

Из этого уравнения следует, что при движении шарика его потенциальная и кинетическая энергия менялась. При этом кинетическая энергия возросла на столько же, на сколько уменьшилась потенциальная.

После перестановки членов в последнем уравнении получим:

(1)

Уравнение, записанное в таком виде, свидетельствует о том, что полная механическая энергия шарика при его движении остаётся постоянной.

Оно может быть записано и так:

Уравнения (1) и (2) представляют собой математическую запись закона сохранения механической энергии.

Таким образом, мы теоретически доказали, что полная механическая энергия тела (точнее, замкнутой системы тел шарик — Земля) сохраняется, т. е. не меняется с течением времени.

Рассмотрим применение закона сохранения механической энергии для решения задач.

Пример 1. Яблоко массой 200 г падает с дерева с высоты 3 м. Какой кинетической энергией оно будет обладать на высоте 1 м от земли?

Пример 2. Мяч бросают вниз с высоты h₁ = 1,8 м со скоростью v₁ = 8 м/с. На какую высоту h₂ отскочит мяч после удара о землю? (Потери энергии при движении мяча и его ударе о землю не учитывайте.)

Вопросы

Что называется механической (полной механической) энергией?
Сформулируйте закон сохранения механической энергии. Запишите его в виде уравнений.
Может ли меняться с течением времени потенциальная или кинетическая энергия замкнутой системы?

Упражнение 22

Решите рассмотренную в параграфе задачу из примера 2 без использования закона сохранения механической энергии.
Оторвавшаяся от крыши сосулька падает с высоты h = 36 м от земли. Какую скорость v она будет иметь на высоте h = 31 м? (Принять g = 10 м/с 2 .)
Шарик вылетает из детского пружинного пистолета вертикально вверх с начальной скоростью v₀ = 5 м/с. На какую высоту от места вылета он поднимется? (Принять g = 10 м/с 2 .)

Задание

Придумайте и проведите простой опыт, наглядно демонстрирующий, что тело движется криволинейно, если скорость движения этого тела и действующая на него сила направлены вдоль пересекающихся прямых. Опишите используемое оборудование, ваши действия и наблюдаемые результаты.

Итоги главы
Самое главное

Ниже даны названия физических законов и их формулировки. Последовательность изложения формулировок законов не соответствует последовательности их названий.

Перенесите в тетрадь названия физических законов и в квадратные скобки впишите порядковый номер формулировки, соответствующей названному закону.

Первый закон Ньютона (закон инерции) [ ];
второй закон Ньютона [ ];
третий закон Ньютона [ ];
закон всемирного тяготения [ ];
закон сохранения импульса [ ];
закон сохранения механической энергии [ ].

Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
Механическая энергия замкнутой системы тел остаётся постоянной, если между телами системы действуют только силы тяготения и силы упругости и отсутствуют силы трения.
Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.
Векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел.
Существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.
Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Проверь себя

Определением скорости прямолинейного равномерного движения является уравнение

Второй закон Ньютона представлен уравнением

Закон всемирного тяготения представлен уравнением

Закон сохранения импульса представлен уравнением

Выполните задания, предложенные в электронном приложении.

Источник

Закон сохранения механической энергии

Удивительно, но закон сохранения механической энергии — базовый закон механики — открыл немецкий корабельный доктор Роберт Юлий Майер, а не ученый-физик. Майеру на момент путешествия было всего 28 лет, во время стоянки корабля в тропическом регионе при кровопускании он наблюдал, что багрово-красная кровь, вытекающая во время процедуры у жителей холодной Европы, в тропиках напоминала алую артериальную.

Майер предположил, что кровь не меняет цвет, поскольку организму в тропическом климате нет необходимости тратить кислород на поддержание

температуры тела. Вернувшись на родину, перед тем как сформулировать закон сохранения механической энергии, Майер продолжил опыты с открытыми на то время разновидностями энергии:

кинетической,
потенциальной,
внутренней,
механической;

. и смог определить, в чем заключается закон сохранения механической энергии.

«Тепло, электричество и перемещение представляют собою феномены, которые могут быть сведены к одной силе, измеряются друг другом и переходят друг в друга по определенным законам» — излагал в своей научной работе Майер.

Кинетическая и потенциальная энергия

Энергия тела — физическая величина, определяющая работу наблюдаемого тела или системы тел за бесконечно долгое время.

В изучении механических явлений рассматривают потенциальную и кинетическую энергии.

Единица энергии в СИ 1 Джоуль (Дж).

Кинетическая энергия — энергия, которой обладает тело в движении (вращении, перемещении в пространстве).

Футбольный мяч, летящий в ворота, летящая в цель стрела, выпущенная метким лучником, едущие с горы сани с сидящим в них хохочущим ребенком — все они во время движения характеризуются кинетической энергией.

Кинетическая энергия напрямую зависит от массы тела и скорости перемещения.

Формула кинетической энергии Е_к = mv 2 /2

Где где m — масса объекта;

v — скорость перемещения объекта в конкретной точке.

Потенциальная энергия. Само по себе тело потенциальной энергией не обладает. Этот вид энергии характеризует взаимосвязь элементов объекта или двух отдельных тел в пространстве.

Стоящие на вершине холма санки, стрела, вложенная лучником в натянутую тетиву, ядро в стволе средневековой пушки — пример объекта, обладающего потенциальной энергией.

Потенциальная энергия бывает положительной или отрицательной относительно определенного условного нулевого уровня, принятого для системы координат:

сила тяжести,
сила упругости,
архимедова сила

Потенциальная энергия объекта зависит от приложенных к нему сил.

Если оценивать расположение объекта в отношении уровня Земли, то потенциальная энергия объекта на поверхности планеты принимается за ноль.

Уравнение Е_п = mɡh поможет рассчитать потенциальную энергию на высоте h:
где m — масса тела;
ɡ — ускорение свободного падения;
h — высота центров масс объектов относительно поверхности планеты;
ɡ = 9,8 м/с 2

Потенциальная энергия упруго деформированного объекта (пружины) рассчитывается согласно уравнению:
Е_п = k·(∆x) 2 /2,
где k — коэффициент жёсткости,
∆x — изменение длины объекта вследствие его сжатия или растяжения.

Суммарное число значений потенциальной и кинетической энергий объекта обозначают как механическая энергия. Для каждого конкретного объекта механическая энергия определяется не выбором системы отсчета, в которой рассчитывают скорость движения исследуемого объекта, а установлением уровня условного нуля для всех видов потенциальных энергий, определенных у данного объекта.

Механическая энергия определяет свойство объекта (системы объектов) совершать работу за счет изменения скорости перемещения объекта или изменения расположения взаимодействующих объектов относительно друг друга.

Источник

Вывести формулу закона сохранения энергии