Вывести рабочую формулу для коэффициента вязкости

Как определить вязкость жидкости методом Стокса?

Формулу определения вязкости Стокс вывел ещё в 1851 году.

Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.

Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.

Всё это и конкретные методы описаны далее в статье.

Содержание статьи

Что такое вязкость

Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.

Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.

По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.

Движение тела в жидкой среде

Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.

Механизм №1 — За твердым телом нет вихрей

Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.

В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).

Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.

Механизм №2 — При движении тела образуются вихри

Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.

Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.

Сила сопротивления

В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.

Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:

где μ – вязкость жидкости;
r – радиус шарика;
υ – скорость равномерного движения шарика.

Условие использования формулы

Существует несколько ограничений для применения формулы Стокса.
1. вязкая среда не ограничена стенками и находится в покое
2. скольжений на границах с твердым телом нет
3. движение жидкости ламинарное
4. радиус круглого тела намного больше, чем длина среднего пробега молекул жидкой среды

Формула вязкости

Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
F_T – сила тяжести;
F_A – сила Архимеда (выталкивающая сила);
T_C – сила лобового сопротивления.

Для круглого шарика сила тяжести будет:

где r –радиус шара;
ρ – плотность шара;
ρ₀ – плотность жидкости;
g – ускорение свободного падения;
υ – скорость равномерного движения шарика;
μ – вязкость жидкости.

В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.

При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:

или подставляя формулы

таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле

Определение вязкости методом Стокса

Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.

На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.

Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.

Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.

Учитывая, что скорость это отношения длины пути ко времени, т.е.:

и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса

Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.

При падении шара радиусом r в трубе радиусом R₀ и высотой h формула будет выглядеть

Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом Стокса требует значения таких параметров, как:
плотность материала шарика;
плотность жидкости;
радиус шарика;
радиус сосуда;
скорость движения шарика.

Видео про методы определения вязкости

Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.

Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.

Но независимо от метода общими остаются:
1. результат измерение не должен зависеть от линейных размеров вискозиметра.
2. не должно быть пристеночного скольжения жидкости.
3. поток жидкости в используемом вискозиметре должен быть ламинарным.

Источник

Вывод рабочей формулы. Одним из способов определения коэффициента вязкости жидкости является метод Стокса

Одним из способов определения коэффициента вязкости жидкости является метод Стокса. Он основан на определении силы сопротивления, действующей на свободно падающий в жидкости металлический шарик.

На шарик, падающий в жидкости, действуют три силы: сила тяжести =mg, сила вязкого трения (сопротивления) и выталкивающая сила (архимедова сила). С увеличением скорости сила сопротивления возрастает и с некоторого момента шарик станет двигаться равномерно. Условие равномерного падения шарика в жидкости

.

Свяжем ось OУ с направлением движения шарика. Тогда уравнение движения шарика в проекции на эту ось принимает вид:

При движении шарика в жидкости играет роль трение отдельных слоев жидкости друг о друга, так как ближайший к поверхности шарика слой жидкости имеет ту же скорость, что и шарик – жидкость прилипает к нему. Другие же слои имеют тем меньшую скорость, чем дальше находятся они от шарика. Поэтому сила сопротивления движению шарика будет зависеть не только от его скорости и размеров, но и от вязкости жидкости.

По закону Стокса сила сопротивления прямо пропорциональна первой степени скорости, коэффициенту вязкости и линейным размерам тела. Для шара движущегося в вязкой жидкости, по закону Стокса сила сопротивления

где η – коэффициент вязкости жидкости; r – радиус шара; υ – скорость его движения.

Выряжая массу шарика и выталкивающую силу через соответствующие плотности, и размеры шарика, а также скорость шарика через пройденный путь и время, получим рабочую формулу

(1)

где ρ – плотность шарика (ρ =7800 кг/м 3 ); ρ_ж – плотность жидкости (ρ_ж=1260 кг/м 3 ); d – диаметр шарика; t – время движения шарика; l – путь, пройденный шариком за время t при равномерном движении; g – ускорение свободного падения.

Порядок выполнения работы

1. Бросьте шарик в цилиндрический сосуд (рис.2) и определить на глаз точку, начиная с которой шарик начинает двигаться равномерно. Установить верхнюю метку на 2-3 см ниже этой точки. Рулеткой или линейкой измерить расстояние между верхней К и нижней N метками.

2. Микрометром измерить диаметр d стального шарика. Измерение повторить не менее пяти раз в разных направлениях.

3. Опустить шарик в жидкость в центре цилиндра и внимательно следить за его прохождением мимо метки К. Глаз при этом должен фиксировать совпадение метки по всей окружности цилиндра. Включить секундомер в момент прохождения шариком метки К и выключить его в момент прохождения шариком метки N. Показания секундомера занести в таблицу. Шарик вытащить из жидкости при помощи магнита. Опыт повторить 5 раз.

Результаты записать в таблицу

№ п.п.	l, м	d, м	t, с	η,кг/м·с	Δη,кг/м·с	ε, %
Середнее значение

1. По формуле (1) вычислить значение η, подставляя значения d и l. Данные занести в таблицу 1.

2. Определить среднее значение измеренных величин.

3. Определить среднее значение коэффициента вязкости:

.

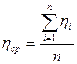
4. Определить абсолютною погрешность отдельного косвенного измерения:

,

где Δd = 0,01 мм; Δl= 0,5 мм; Δt= 0,01 с.

5. Определить среднее значение абсолютной погрешности:

.

6. Подсчитать относительную погрешность измерения:

.

7. Полученный результат представить в виде

1. Запишите формулу для силы вязкого трения.

2. Какой физический смысл имеет коэффициент вязкости?

3. Как зависит коэффициент внутреннего трения газов и жидкостей
от температуры? Объясните эту зависимость на основе молекулярно-кинетической теории строения вещества.

4. В чем различие механизма возникновения внутреннего трения в газах и жидкостях?

5. Объясните механизм возникновения силы внутреннего трения, действующей на шарик, который движется в вязкой среде.

6. Как изменяется скорость шарика при падении в жидкости?

8. Выведите формулу для расчета коэффициента вязкости.

9. В чем сущность использованного в работе определения вязкости.

Источник

Коэффициент вязкости — формулы, виды и размерность величины

Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.

Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.

Коэффициент динамической вязкости

Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.

Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:

Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.

Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:

τ – касательное напряжение;

µ — показатель пропорциональности, который является динамическим индексом вещества.

Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.

Коэффициент динамической вязкости газа

Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:

Коэффициент вязкости жидкостей

Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.

Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.

Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.

Связь коэффициента вязкости с числами Рейнольдса и силой трения

Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.

Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.

Примеры решения задач

Попробуем решить следующую задачу.

Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м 3 . Абсолютный индекс составляет 1•10 -3 Па*с.

Следует узнать эквивалентный диаметр сечения межтрубного пространства:

Определение скорости воды на основе уравнения расхода:

По формуле Рейнольдса найти число Re:

Подставляя значения, получаем:

Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.

Коэффициент кинематической вязкости

Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.

Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:

Действие 4. Вычисление кинематического показателя, исходя из формулы:

Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.

Заключение

Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.

Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:

Источник