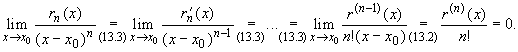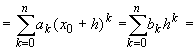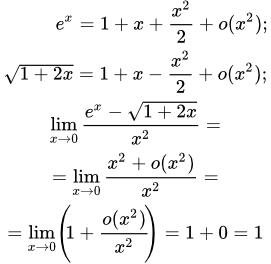Вывести разложение тейлора для
Рассмотрим следующую задачу. Пусть функция y = f(x) имеет в точке x0 производные до порядка n включительно. Требуется найти такой многочлен Pn(x) степени не выше, чем n, что
(x0) = f (k) (x), k = 0, 1, . n,
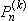
rn(x) 
f(x) — Pn(x) = o((x — x0) n ), x
x0.
В случае n = 1 нам уже известно, что эта задача имеет решение и что ее решением является многочлен
P1(x) = f(x0) + f’(x0)(x — x0),
P1(x) = f(x0), P’1(x) = f’(x0),
r1(x) = f(x) — P1(x) = f(x) — f(x0) — f’(x0)(x — x0) =
= 
y — f’(x0)x = y — dy = o(x), x0,
где, как обычно, x = x — x0, y = f(x) — f(x0).
По аналогии с формулой (14.3) будем искать многочлен Pn(x), удовлетворяющий условиям (14.1) и (14.2), в виде
Pn(x) = a0 + a1(x — x0) + . + an(x — x0) n .
Положив x = x0, в силу условия (14.1) при k = 0 получим
Дифференцируя равенство (14.4), будем иметь
Положив здесь x = x0, в силу условия (14.1) при k = 1 получим
Вообще, продифференцировав равенство (14.4) k раз:
(x) = k!ak + (k + 1). 2ak+1(x — x0) + . + n(n — 1). (n — k + 1)an(x — x0) n—k ,
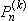
и положив x = x0, в силу условия (14.1) получим
ak = f (k) (x0)/k! k = 0, 1, . n,
Таким образом, если коэффициенты многочлена (14.4) выбраны согласно формулам (14.7), то этот многочлен удовлетворяет условию (14.1). Покажем, что он удовлетворяет и условию (14.2). Для этого прежде всего отметим, что в силу условий (14.1) для функции
rn(x) f(x) — Pn(x)
rn(x0) = r’n(x0) =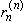 
(x0) = 0.
Из того, что функция f(x) имеет в точке x0 производную порядка n, вытекает, что у нее в некоторой окрестности этой точки существуют производные до порядка n — 1 включительно и все производные функции f(x), а следовательно, в силу равенства (14.8) и производные функции rn(x), до порядка n — 1 включительно непрерывны в указанной точке x0 и
(x) = r (k) (x0)
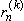
Для вычисления предела 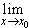[rn(x)/(x — x0) n ] применим сначала n — 1 раз правило Лопиталя — теорему 2 из п. 13.1, а затем оттуда же теорему 1:
Это и означает выполнение условия (14.2). Итак, доказана следующая
Теорема 1. Если функция f(x) n раз дифференцируема в точке x0, то в некоторой окрестности этой точки
xx0.
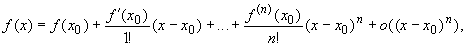
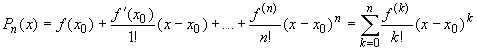
называется многочленом Тейлора (порядка n), формула (14.10) — формулой Тейлора (порядка n) для функции f(x) в точке x = x0, а функция
rn(x) = f(x) — Pn(x)
— остаточным членом (порядка n) формулы Тейлора, а его представление в виде (14.2), т. е.
rn(x) = o((x — x0) n ), xx0,
— записью остаточного члена в виде Пеано.
Частный случай формулы Тейлора (14.10) при x0 = 0 называется формулой Маклорена
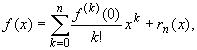
где, согласно (14.2), остаточный член rn(x) можно записать в виде
rn(x) = o(x) n , x0.
Из нижеследующей теоремы будет следовать, что многочлен Тейлора единствен в своем роде. Именно, никакой другой многочлен не приближает функцию, заданную в окрестности точки x0 с точностью до бесконечно малых того же порядка относительно x — x0, xx0, что и многочлен Тейлора.
Предварительно отметим, что любой многочлен Pn(x) =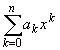 
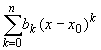
степени n для любого x0 может быть записан в виде Pn(x) = 
. Действительно, положив h = x — x0, использовав формулу бинома Ньютона и собрав члены с одинаковыми степенями h, получим
Pn(x) =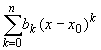 
,
где bk — некоторые постоянные.
Теорема 2. Если функция f(x) задана в окрестности точки x0 и имеет представление
f(x) =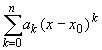
+ o((x — x0) n ), xx0,
то такое представление единственно. 
Пусть наряду с представлением (14.15) имеет место представление
f(x) =+ o((x — x0) n ), xx0,
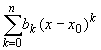
ck = bk — ak, k = 0, 1, . n,
и вычтя из равенства (14.16) равенство (14.15), получим
+ o((x — x0) n ) = 0, xx0,
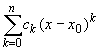
Перейдя в этом равенстве к пределу при xx0, получим c0 = 0.
Заметим, что o((x — x0) m ) = 
(x)(x — x0) m , (x) = 0, и, следовательно, при x
x0, m = 1, 2, .
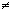
o((x — x0) m )/ (x — x0) = (x)(x — x0) m-1 = o((x — x0) m-1 ), xx0.
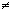
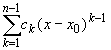
Сократив на x — x0, xx0, левую часть равенства (14.18) (в нем, как уже доказано, c0 = 0), получим
+ o((x — x0) n-1 ) = 0, xx0.
Перейдя в этом равенстве к пределу при xx0, xx0, получим c1 = 0. Продолжая этот процесс после m-го шага, 0 n-m ) = 0, xx0.
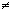
отсюда при xx0 следует, что cm = 0, m = 0, 1, . n.
Таким образом, в силу равенств (14.17)
ak = bk, m = 0, 1, . n. 
Теорема 2 называется обычно теоремой единственности. Из нее следует, что если для n раз дифференцируемой в точке функции f получено представление ее в виде (14.15), то это представление является ее разложением по формуле Тейлора. В самом деле, при сделанных предположениях, согласно теореме 1, такое представление существует, а другого в силу теоремы 2 нет.
Источник
Решение пределов, используя ряд Тейлора
Метод решения
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов является разложение функций в степенной ряд Тейлора. Применение этого метода состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 при переменной x , стремящейся к нулю. Для этого, если требуется, выполняем преобразования и делаем замену переменной.
2) Раскладываем числитель и знаменатель в ряд Тейлора в окрестности точки x = 0 . При этом выполняем разложение до такой степени x n , которая необходима для устранения неопределенности. Остальные члены включаем в o ( x n ) .
Этот метод применим, если после выполнения пункта 1), функции в числителе и знаменателе можно разложить в степенной ряд.
Выполнять разложение сложных функций и произведения функций удобно по следующей схеме. А) Задаемся показателем степени n , до которого мы будем проводить разложение.
Б) Применяем приведенные ниже формулы разложения функций в ряд Тейлора, сохраняя в них члены до включительно, и отбрасывая члены с при , или заменяя их на .
В) В сложных функциях делаем замены переменных так, чтобы аргумент каждой ее части стремился к нулю при . Например,
.
Здесь при . Тогда можно использовать разложение функции в окрестности точки .
Примечание. Разложение функции в ряд Тейлора, в окрестности точки , называется рядом Маклорена. Поэтому для применяемых в наших целях рядов уместны оба названия.
Применяемые свойства о малого
Определение и доказательство свойств о малого приводится на странице: «О большое и о малое. Сравнение функций». Здесь мы приводим свойства, используемые при решении пределов разложением в ряд Маклорена (то есть при ).
Далее m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.
Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .
Разложение элементарных функций в ряд Тейлора (Маклорена)
Далее приводятся разложения элементарных функций в степенной ряд при . Как мы упоминали ранее, ряд Тейлора в окрестности точки называется рядом Маклорена.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью ряда Тейлора.
⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Вычислить предел последовательности, используя разложение в ряд Тейлора.
.
Это неопределенность вида бесконечность минус бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого выполняем преобразования.
.
Здесь мы учли, что номер элемента последовательности n может принимать только положительные значения. Поэтому . Делаем замену переменной . При . Будем искать предел считая, что x – действительное число. Если предел существует, то он существует и для любой последовательности , сходящейся к нулю. В том числе и для последовательности .
.
Раскладываем функцию в числителе в ряд Тейлора. Применяем формулу:
.
Оставляем только линейный член.
.
.
Здесь мы учли, что поскольку существует двусторонний предел , то существуют равные ему односторонние пределы. Поэтому .
Пример 2
Все примеры ⇑ Показать, что значение второго замечательного предела можно получить, используя разложение в ряд Тейлора.
Делаем замену переменной . Тогда . При . Подставляем.
.
Для вычисления предела можно считать, что значения переменной t принадлежат любой, наперед выбранной, проколотой окрестности точки . Мы полагаем, что . Используем то, что экспонента и натуральный логарифм являются обратными функциями по отношению друг к другу. Тогда
.
Вычисляем предел в показателе, используя следующее разложение в ряд Тейлора:
.
.
Поскольку экспонента является непрерывной функцией для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.
Пример 3
Все примеры ⇑ Вычислить предел, используя разложение в ряд Тейлора.
.
Это неопределенность вида 0/0 . Используем следующие разложения функций в окрестности точки :
;
;
.
Раскладываем с точностью до квадратичных членов:
;
.
Делим числитель и знаменатель на и находим предел:
.
Пример 4
Все примеры ⇑ Решить предел с помощью ряда Тейлора.
.
Легко видеть, что это неопределенность вида 0/0 . Раскрываем ее, применяя разложения функций в ряд Тейлора. Используем приведенное выше разложение для гиперболического синуса ⇑:
(П4.1) .
В разложении экспоненты, заменим x на –x :
(П4.2) .
Далее, – сложная функция. Сделаем замену переменной . При . Поэтому мы можем используем разложение натурального логарифма в окрестности точки . Используем приведенное выше разложение, в котором переименуем переменную x в t :
(П4.3) .
Заметим, что если бы у нас была функция , то при . Поэтому подставить в предыдущее разложение нельзя, поскольку оно применимо в окрестности точки . В этом случае нам потребовалось бы выполнить следующее преобразование:
.
Тогда при и мы могли бы применить разложение (П4.3).
Попробуем решить предел, выполняя разложение до первой степени переменной x : . То есть оставляем только постоянные члены, не зависящие от x : , и линейные . Остальные будем отбрасывать. Точнее переносить в .
;
;
.
Поскольку , то в разложении логарифма мы отбрасываем члены, начиная со степени 2. Применяя, приведенные выше свойства о малого имеем:
.
Подставляем в предел:
.
Мы снова получили неопределенность вида 0/0 . Значит разложения до степени не достаточно.
Если мы выполним разложение до степени , то опять получим неопределенность:
.
Выполним разложение до степени . То есть будем оставлять только постоянные члены и члены с множителями . Остальные включаем в .
;
;
;
.
Далее замечаем, что . Поэтому в разложении логарифма нужно отбросить члены, начиная со степени , включив их в . Используем разложение (П4.3), заменив t на :
.
Подставляем в исходную функцию.
.
Находим предел.
.
Пример 5
Все примеры ⇑ Найти предел с помощью ряда Тейлора.
.
Будем проводить разложение числителя и знаменателя в ряд Маклорена до четвертой степени включительно.
Теперь переходим к числителю. При . Поэтому сделать подстановку и применить разложение для нельзя, поскольку это разложение применимо при , а у нас . Заметим, что . Поэтому выполним преобразование.
.
Теперь можно сделать подстановку , поскольку при .
Разложим функцию и ее степени в ряд Тейлора в окрестности точки . Применяем приведенное выше разложение ⇑.
;
;
;
;
;
;
Далее заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .
Разложим второй логарифм. Приводим его к виду , где при .
,
где .
Разложим z в ряд Тейлора в окрестности точки с точностью до .
Применим разложение синуса ⇑:
.
Заменим x на :
. Тогда
;
;
Заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .
Раскладываем с точностью до и учитываем, что .
;
.
Подставляем разложение числителя и знаменателя и находим предел.
;
.
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов . Опубликовано: 29-04-2019
Источник
