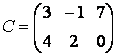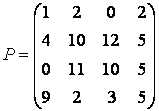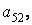Вывести строку матрицы матлаб

Документация

Матрицы в среде MATLAB

Эта тема содержит введение в создание матриц и выполнение основных матричных вычислений в MATLAB ® .

Среда MATLAB использует термин матрица , чтобы указать на переменное, содержащее вещественные или комплексные числа, расположенные в двумерной сетке. Массив является, в более общем плане, вектором, матрицей или более высокой размерной сеткой чисел. Все массивы в MATLAB являются прямоугольными, в том смысле, что векторы компонента по любому измерению являются всеми одинаковыми длина. Математические операции, заданные на матрицах, являются предметом линейной алгебры.

Создание матриц

MATLAB имеет много функций, которые создают различные виды матриц. Например, можно создать симметрическую матрицу с записями на основе треугольника Паскаля:

Или, можно создать несимметричную матрицу магического квадрата , которая имеет равные суммы строки и столбца:

Другим примером является 3 2 прямоугольная матрица случайных целых чисел. В этом случае первый вход к randi описывает область значений возможных значений для целых чисел, и вторые два входных параметров описывают количество строк и столбцов.

Вектор-столбцом является m-by-1 матрица, вектор-строка является 1 n матрицей, и скаляр является матрицей 1 на 1. Чтобы задать матрицу вручную, используйте квадратные скобки [ ] обозначить начало и конец массива. В скобках используйте точку с запятой ; обозначить конец строки. В случае скаляра (матрица 1 на 1), не требуются скобки. Например, эти операторы производят вектор-столбец, вектор-строку и скаляр:

Для получения дополнительной информации о создании и работе с матрицами, смотрите Создание, конкатенацию и расширение матрицы.

Сложение и вычитание матриц

Сложение и вычитание матриц и массивов выполняются поэлементно или поэлементные . Например, добавление A к B и затем вычитание A от результата восстанавливает B :

Сложение и вычитание требуют, чтобы обе матрицы имели совместимые размерности. Если размерности несовместимы, ошибка заканчивается:

Для получения дополнительной информации см. Массив по сравнению Матричные операции.

Векторные произведения и транспонирование

Вектор-строка и вектор-столбец той же длины могут быть умножены в любом порядке. Результатом является или скаляр, названный скалярным произведением , или матрица, названная векторным произведением :

Для действительных матриц транспонировать операция обменивается a _{i j} и a _{j i}. Для комплексных матриц другой фактор состоит в том, взять ли сопряженное комплексное число комплексных записей в массиве, чтобы сформировать комплексное сопряженное транспонирование . MATLAB использует оператор апострофа ( ‘ ) выполнять комплексное сопряженное транспонирование и оператор точечного апострофа ( .’ ) транспонировать без спряжения. Для матриц, содержащих все действительные элементы, эти два оператора возвращают тот же результат.

Матрица в качестве примера A = pascal(3) симметрично , таким образом , A’ равно A . Однако B = magic(3) не симметрично, таким образом , B’ отразили элементы по основной диагонали:

Для векторов перемещение превращает вектор-строку в вектор-столбец (и наоборот):

Если x и y оба действительные вектор-столбцы, затем продукт x*y не задан, но эти два продукта

приведите к тому же скалярному результату. Это количество используется так часто, оно имеет три различных имени: скалярное произведение , скалярное произведение или скалярное произведение . Существует даже специализированная функция для названных скалярных произведений dot .

Для комплексного вектора или матрицы, z , количество z’ не только транспонирует вектор или матрицу, но также и преобразует каждый комплексный элемент в его сопряженное комплексное число. Таким образом, знак мнимой части каждого комплексного элемента изменения. Например, рассмотрите комплексную матрицу

Комплексное сопряженное транспонирование z :

Неспрягаемый комплекс транспонирует, где комплексная часть каждого элемента сохраняет свой знак, обозначается z.’ :

Для комплексных векторов, эти два скалярных произведения x’*y и y’*x сопряженные комплексные числа друг друга и скалярное произведение x’*x из комплексного вектора с собой действительно.

Умножение матриц

Умножение матриц задано способом, который отражает состав базовых линейных преобразований и позволяет компактное представление систем одновременных линейных уравнений. Матричное произведение C = AB задан, когда размерность столбца A равна размерности строки B, или когда один из них является скаляром. Если A является m-by- p, и B является p-by- n, их продукт , C является m-by- n. Продукт может на самом деле быть задан с помощью MATLAB for циклы, colon обозначение и векторные скалярные произведения:

MATLAB использует звездочку, чтобы обозначить умножение матриц, как в C = A*B . Умножение матриц не является коммутативным; то есть, A*B обычно не равно B*A :

Матрица A может быть умножена справа вектор-столбцом и слева вектором-строкой:

Прямоугольные умножения матриц должны удовлетворить условиям совместимости размерности. Начиная с A имеет размер 3х3 и C 3 2, можно умножить их, чтобы добраться 3 2 результат (общие внутренние отмены размерности):

Однако умножение не работает в обратном порядке:

Можно умножить что-либо со скаляром:

Когда вы умножаете массив на скаляр, скаляр неявно расширяется, чтобы быть одного размера с другим входом. Это часто упоминается как скалярное расширение .

Единичная матрица

Общепринятое математическое обозначение использует прописную букву I, чтобы обозначить единичные матрицы, матрицы различных размеров с единицами на основной диагонали и нулях в другом месте. Эти матрицы имеют свойство, что A I = A и I A = A каждый раз, когда размерности совместимы.

Исходная версия MATLAB не могла использовать I с этой целью, потому что это не различало прописные и строчные буквы, и i уже служил индексом и как комплексной единицей. Таким образом, английская игра слов языка была введена. Функция

возвращает m-by- n прямоугольная единичная матрица и eye(n) возвращает n-by- n квадратная единичная матрица.

Обращение матриц

Если матричный A является квадратным и несингулярным (ненулевой определитель), затем уравнения A X = I и X A = , I имеет то же решение X. Это решение называется инверсией A и обозначается A -1 . inv функционируйте и выражение A^-1 оба вычисляют обратную матрицу.

Определитель , вычисленный det мера масштабного коэффициента линейного преобразования, описанного матрицей. Когда определитель ниже нуля, матрица сингулярна , и никакая инверсия не существует.

Некоторые матрицы почти сингулярны , и несмотря на то, что обратная матрица существует, вычисление восприимчиво к числовым ошибкам. cond функция вычисляет число обусловленности для инверсии , которая дает индикацию относительно точности результатов матричной инверсии. Число обусловленности лежит в диапазоне от 1 для численно устойчивой матрицы к Inf для сингулярной матрицы.

Редко необходимо сформировать явную инверсию матрицы. Частое неправильное употребление inv возникает при решении системы линейных уравнений A x = b . Лучший способ решить это уравнение, с точки зрения и времени выполнения и числовой точности, состоит в том, чтобы использовать матричный оператор обратной косой черты x = A\b . Смотрите mldivide для получения дополнительной информации.

Продукт тензора Кронекера

Кронекеров продукт, kron(X,Y) , из двух матриц большая матрица, сформированная из всех возможных продуктов элементов X с теми из Y . Если X m-by- n и Y p-by- q, затем kron(X,Y) mp-by- nq. Элементы располагаются таким образом что каждый элемент X умножается на целый матричный Y :

Кронекеров продукт часто используется с матрицами нулей и единиц, чтобы создать повторенные копии маленьких матриц. Например, если X матрица 2 на 2

и I = eye(2,2) единичная матрица 2 на 2, затем:

Кроме kron , некоторые другие функции, которые полезны, чтобы реплицировать массивы, repmat , repelem , и blkdiag .

Векторные и матричные нормы

p — норма векторного x,

‖ x ‖ p = ( ∑ | x i | p ) 1 p ,

вычисляется norm(x,p) . Эта операция задана для любого значения p> 1, но наиболее распространенные значения p равняются 1, 2, и ∞. Значением по умолчанию является p = 2, который соответствует Евклидовой длине или векторной величине :

p — норма матричного A,

‖ A ‖ p = max x ‖ A x ‖ p ‖ x ‖ p ,

может быть вычислен для p = 1, 2, и ∞ norm(A,p) . Снова, значением по умолчанию является p = 2:

В случаях, где вы хотите вычислить норму каждой строки или столбца матрицы, можно использовать vecnorm :

Используя многопоточное вычисление с функциями линейной алгебры

MATLAB поддерживает многопоточный расчет во многой линейной алгебре и поэлементных числовых функциях. Эти функции автоматически выполняются на нескольких потоках. Для функции или выражения, чтобы выполниться быстрее на нескольких центральных процессорах, много условий должны быть верными:

Функция выполняет операции, что легко раздел в разделы, которые выполняются одновременно. Эти разделы должны смочь выполниться с небольшой связью между процессами. Они должны потребовать немногих последовательных операций.

Размер данных является достаточно большим так, чтобы любые преимущества параллельного выполнения перевесили время, требуемое разделить данные и управлять отдельными потоками выполнения. Например, большинство функций убыстряется только, когда массив содержит несколько тысяч элементов или больше.

Операция не ограничена памятью; время вычислений не во власти времени доступа к памяти. Как правило сложные функции ускоряют больше, чем простые функции.

Матрица умножает (X*Y) и матричная степень (X^p) операторы показывают значительное увеличение скорости на больших массивах с двойной точностью (порядка 10 000 элементов). Функции анализа матрицы det , rcond , hess , и expm также покажите значительное увеличение скорости на больших массивах с двойной точностью.

Источник

Урок 6 — Матрицы. Работа с матрицами в MatLab. Примеры

1. Различные способы ввода матриц в пакете MatLab

Вводить небольшие по размеру матрицы удобно прямо из командной строки. Введите матрицу размерностью два на три

.

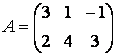
Для хранения матрицы используйте двумерный массив с именем A. При вводе учтите, что матрицу А можно рассматривать как вектор-столбец из двух элементов, каждый из которых является вектор-строкой длиной три, следовательно, строки при наборе отделяются точкой с запятой:

» А = [3 1 -1; 2 4 3]
А =
3 1 -1
2 4 3

Для изучения простейших операций над матрицами приведем еще несколько примеров. Рассмотрим другие способы ввода. Введите квадратную матрицу размера три так, как описано ниже:

.

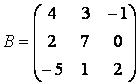
Начните набирать в командной строке

Нажмите клавишу . Обратите внимание, что пакет ничего не вычислил. Курсор мигает на следующей строке без символа ». Продолжите ввод матрицы построчно, нажимая в конце каждой строки . Последнюю строку завершите закрывающей квадратной скобкой, получается:

2 7 0
-5 1 2]
B =
4 3 -1
2 7 0
-5 1 2

Еще один способ ввода матриц состоит в том, что матрицу можно трактовать как вектор-строку, каждый элемент которой является вектор-столбцом. Например, матрицу два на три

можно ввести при помощи команды:

» С = [[3; 4] [-1; 2] [7; 0]]
С =
3 -1 7
4 2 0

Посмотрите переменные рабочей среды, набрав в командной строке whos:

А 2×3 48 double array
В 3×3 72 double array
С 2×3 48 double array

Итак, в рабочей среде содержится три матрицы, две прямоугольные и одна квадратная.

2. Обращение к элементам матриц в пакете MatLab

Доступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например

Элементы матриц могут входить в состав выражений:

» С(1, 1) + С(2, 2) + С(2, 3)
ans =
5

Расположение элементов матрицы в памяти компьютера определяет еще один способ обращения к ним. Матрица А размера m на n хранится в виде вектора длины mn, в котором элементы матрицы расположены один за другим по столбцам

[А(1,1) А(2,1) . А(m,1) . А(1,n) А(2,n) . А(m,n)].

Для доступа к элементам матрицы можно использовать один индекс, задающий порядковый номер элемента матрицы в векторе.
Матрица С, определенная в предыдущем подразделе, содержится в векторе

[C(1,1) C(2,1) C(1,2) С(2,2) С(1,3) С(2,3)],

который имеет шесть компонент. Доступ к элементам матрицы осуществляется следующим образом:

3. Операции над матрицами в пакете MatLab: сложение, вычитание, умножение, транспонирование и возведение в степень

При использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус. Найдите сумму и разность матриц С и А, определенных выше:

» S = А+С
S =
6 0 6
6 6 3
» R = С — А
R =
0 -2 8
2 -2 -3

Следите за совпадением размерности, иначе получите сообщение об ошибке:

» S = А+В
. Error using ==> ±
Matrix dimensions must agree.

Для умножения матриц предназначена звездочка:

» Р = С*В
P =
-25 9 11
20 26 -4

Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева:

» Р = А*3
Р =
9 3 -3
6 12 -3
» Р = 3*А
Р =
9 3 -3
6 12 9

Транспонирование матрицы, так же как и вектора, производится при помощи .’, а символ ‘ означает комплексное сопряжение. Для вещественных матриц эти операции приводят к одинаковым результатам:

» В’
ans =
4 2 -5
3 7 1
-1 0 2

» В.’
ans =
4 2 -5
3 7 1
-1 0 2

Замечание 1

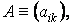
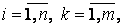
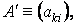
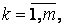
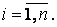
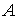
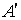
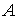
Если матрица есть произвольная матрица размера n m, то матрица, транспонированная по отношению к А,есть матрица размера m n: Таким образом, строки матрицы становятся столбцами матрицы , а столбцы матрицы становятся строками матрицы .
Комплексно-сопряженная матрица получается из исходной в два этапа: выполняется транспонирование исходной матрицы, а затем все комплексные числа заменяются на комплексно-сопряженные.

Сопряжение и транспонирование матриц, содержащих комплексные числа, приведут к созданию разных матриц:

»K= [l-i, 2+3i; 3-5i, l-9i]
К = 1.0000 – 1.0000i 2.0000 + 3.0000i
3.0000 – 5.0000i 1.0000 – 9.0000i
»K’
ans =
1.0000 + 1.0000i 3.0000 + 5.0000i
2.0000 – 3.0000i 1.0000 + 9.0000i

» K.’
ans =
1.0000 — 1.0000i 3.0000 — 5.0000i
2.0000 + 3.0000i 1.0000 — 9.0000i

Замечание 2

При вводе вектор-строк их элементы можно разделять или пробелами, или запятыми. При вводе матрицы К применены запятые для более наглядного разделения комплексных чисел в строке.

Возведение квадратной матрицы в целую степень производится с использованием оператора ^:

» В2 = В^2
B2 =
27 32 -6
22 55 -2
-28 -6 9

Проверьте полученный результат, умножив матрицу саму на себя.
Убедитесь, что вы освоили простейшие операции с матрицами в MatLab. Найдите значение следующего выражения

Учтите приоритет операций, сначала выполняется транспонирование, потом возведение в степень, затем умножение, а сложение и вычитание производятся в последнюю очередь.

»(А+С)*В^3*(А-С)’
ans =
1848 1914
10290 3612

4. Умножение матриц и векторов

Вектор-столбец или вектор-строка в MatLab являются матрицами, у которых один из размеров равен единице, поэтому все вышеописанные операции применимы и для умножения матрицы на вектор-столбец или вектор-строки на матрицу. Например, вычисление выражения

можно осуществить следующим образом:

» a = [1 3 -2];
» B = [2 0 1; -4 8 -1; 0 9 2];
» c = [-8; 3; 4];
» a*B*c
ans =
74

5. Блочные матрицы

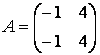
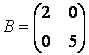
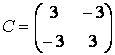
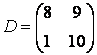
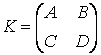
Очень часто в приложениях возникают так называемые блочные матрицы, т.е. матрицы, составленные из непересекающихся подматриц (блоков). Рассмотрим вначале конструирование блочных матриц. Введите матрицы: , , , и создайте из них блочную матрицу .
Учитывая, что матрица К состоит из двух строк, в первой строке матрицы А и B, а во второй — С и D, блочную матрицу можно сформировать следующим образом:

» К = [А В; С D]
K =
-1 4 2 0
-1 4 0 5
3 -3 8 9
-3 3 1 10

Блочную матрицу можно получить и другим способом, если считать, что матрица К состоит из двух столбцов, в первом — матрицы А и С, а во втором — В и D:

Обратной задачей к конструированию блочных матриц является задача выделения блоков. Выделение блоков матриц осуществляется индексацией при помощи двоеточия. Введите матрицу

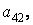
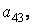
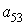
и затем выделите подматрицу с элементами , задав номера строк и столбцов при помощи двоеточия:

»Р1 = Р(2:3,2:3)
Р1 =
10 12
11 10

Для выделения из матрицы столбца или строки (то есть массива, у которого один из размеров равен единице) следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием без указания пределов. Например, запишите вторую строку матрицы Р в вектор р

»p = P(2, 🙂
p =
4 10 12 5

При выделении блока до конца матрицы можно не указывать ее размеры, а использовать элемент end:

»p = Р(2, 2:end)
p =
10 12 5

6. Удаление строк и столбцов

В MatLab парные квадратные скобки [ ] обозначают пустой массив, который, в частности, позволяет удалять строки и столбцы матрицы. Для удаления строки следует присвоить ей пустой массив. Удалите, например, первую строку квадратной матрицы:

» М = [2 0 3
1 1 4
6 1 3];
» M(1,:)=[];
» M
M =
1 1 4
6 1 3

Обратите внимание на соответствующее изменение размеров массива, которое можно проверить при помощи size:

Аналогичным образом удаляются и столбцы. Для удаления нескольких идущих подряд столбцов (или строк) им нужно присвоить пустой массив. Удалите второй и третий столбец в массиве M

Индексация существенно экономит время при вводе матриц, имеющих определенную структуру.

7. Заполнение матриц при помощи индексации

Выше было описано несколько способов ввода матриц в MatLab. Однако часто бывает проще сгенерировать матрицу, чем вводить ее, особенно если она обладает простой структурой. Рассмотрим пример такой матрицы:

.

Генерация матрицы Т осуществляется в три этапа:
1. Создание массива T размера пять на пять, состоящего из нулей.
2. Заполнение первой строки единицами.
3. Заполнение части последней строки минус единицами до последнего элемента.
Соответствующие команды MatLab приведены ниже.

» A(1:5, 1:5) = 0
A=
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(1, 🙂 = 1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(end, 3:end) = -1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 -1 -1 -1

Создание некоторых специальных матриц в MatLab осуществляется при помощи встроенных функций.

8. Создание матриц специального вида

Заполнение прямоугольной матрицы нулями производится встроенной функцией zeros, аргументами которой являются число строк и столбцов матрицы:

» A = zeros(3, 6)
A =
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0

Один аргумент функции zeros приводит к образованию квадратной матрицы заданного размера:

» A = zeros(3)
A =
0 0 0
0 0 0
0 0 0

Единичная матрица инициализируется при помощи функции eye:

» I = eye(4)
I=
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Функция eye с двумя аргументами создает прямоугольную матрицу, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю:

» I = eye(4, 8)
I =
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0

Матрица, состоящая из единиц, образуется в результате вызова функции
ones:

» E = ones(3, 7)
E =
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1

Использование одного аргумента в ones приводит к созданию квадратной матрицы, состоящей из единиц.

MatLab предоставляет возможность заполнения матриц случайными элементами. Результатом функции rand является матрица чисел, распределенных случайным образом между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону:

» R = rand(3, 5)
R =
0.9501 0.4860 0.4565 0.4447 0.9218
0.2311 0.8913 0.0185 0.6154 0.7382
0.6068 0.7621 0.8214 0.7919 0.1763

Один аргумент функций rand и randn приводит к формированию квадратных матриц:
Часто возникает необходимость создания диагональных матриц, т.е. матриц, у которых все недиагональные элементы равны нулю. Функция diag формирует диагональную матрицу из вектор-столбца или вектор-строки, располагая их элементы по диагонали матрицы:

» d = [1; 2; 3; 4];
» D = diag(d)
D =
1 0 0 0
0 2 0 0
0 0 3 0
0 0 0 4

Функция diag служит и для выделения диагонали матрицы в вектор, например

» A = [10 1 2; 1 20 3; 2 3 30];
» d = diag(A)
d =
10
20
30

9. Поэлементные операции с матрицами

Поскольку векторы и матрицы хранятся в двумерных массивах, то применение математических функций к матрицам и поэлементные операции производятся так же, как для векторов.
Введите две матрицы

, .

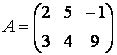
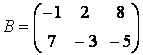
Умножение каждого элемента одной матрицы на соответствующий элемент другой производится при помощи оператора .*:

» С = А.*В
С =
-2 10 -8
21 -12 -45

Для деления элементов первой матрицы на соответствующие элементы второй используется оператор ./, а для деления элементов второй матрицы на соответствующие элементы первой служит .\:

» R1 = А./В1
R1 =
-2.0000 2.5000 -0.1250
0.4286 -1.3333 -1.8000
» R2 = А.\В1
R2 =
-0.5000 0.4000 -8.0000
2.3333 -0.7500 -0.5556

Поэлементное возведение в степень осуществляется при помощи оператора .^. Показатель степени может быть числом или матрицей того же размера, что и матрица, возводимая в степень. Во втором случае элементы первой матрицы возводятся в степени, равные элементам второй матрицы.

10. Визуализация матриц

Матрицы с достаточно большим количеством нулей называются разреженными. Часто необходимо знать, где расположены ненулевые элементы, т.е. получить так называемый шаблон матрицы. Для этого в MatLab служит функция spy. Посмотрим шаблон матрицы G
.

После выполнения команды spy на экране появляется графическое окно Figure No. 1. На вертикальной и горизонтальной осях отложены номера строк и столбцов. Ненулевые элементы обозначены маркерами, внизу графического окна указано число ненулевых элементов (nz = 19).
Наглядную информацию о соотношении величин элементов матрицы дает функция imagesc, которая интерпретирует матрицу как прямоугольное изображение. Каждый элемент матрицы представляется в виде квадратика, цвет которого соответствует величине элемента. Для того чтобы узнать соответствие цвета и величины элемента следует использовать команду colorbar, выводящую рядом с изображением матрицы шкалу цвета (Insert (в графическом окне Figure No. 1), colorbar). Наконец, для печати на монохромном принтере удобно получить изображение в оттенках серого цвета, используя команду colormap(gray) (Edit (в графическом окне Figure No. 1), Colormap, Colormap Editor, Tools, gray). Мы будем работать с матрицей G. Набирайте команды, указанные ниже, и следите за состоянием графического окна:

» imagesc(G)
» colorbar
» colormap(gray)

В результате получается наглядное представление матрицы.

Источник