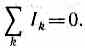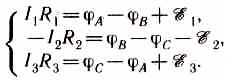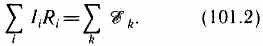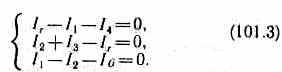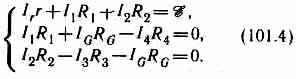Вывести условие равновесия моста уитстона используя правила кирхгофа

Лабораторная работа № 31

Цель работы : 1. Изучение принципа работы измерительной мостовой схемы. 2. Определение величины сопротивления двух проводников и величины сопротивления при их последовательном и параллельном соединении. 3. Определение величины внутреннего сопротивления гальванометра.

Приборы и принадлежности : реохорд, набор резисторов с неизвестными сопротивлениями, магазин сопротивлений, милливольтметр, источник постоянного тока.

Теория R –моста Уитстона

Электрическим мостом в технике измерений называют электрический прибор для измерения сопротивлений, емкостей, индуктивностей и других электрических величин, представляющих собой измерительную мостовую цепь, действие которой основано на методике сравнения измеряемой величины с образцовой мерой. Как известно, метод сравнения дает весьма точные результаты измерений, вследствие чего мостовые схемы получили широкое распространение как в лабораторной, так и в производственной практике.

Классическая мостовая цепь состоит из четырех сопротивлений Z₁, Z₂, Z₃, Z₄, соединенных последовательно в виде четырехугольника (рис. 1), причем точки А, Е, В, D называют вершинами. Ветвь АВ, содержащая источник питания U_n , называется диагональю питания, а ветвь ЕD, содержащая сопротивление нагрузки Z _H , – диагональю нагрузки.. Сопротивления Z₁, Z₂, Z₃, Z₄, включенные между двумя соседними вершинами, называются плечами мостовой цепи.

Название «мостовая цепь» объясняется тем, что диагонали, как мостики, соединяют две противолежащие вершины (диагональ нагрузки, например, ранее так и называлась – мост). Схема, представленная на рис. 1, известна в литературе как четырехплечный мост, или мост Уитстона. В данной лабораторной работе мы познакомимся с работой одной из разновидностей моста Уитстона, а именно с той, которая позволяет проводить измерения величин активных сопротивлений.

Рис. 1

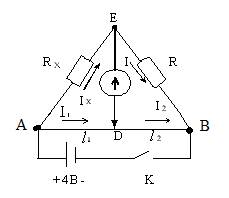
Условие равновесия моста Уитстона. R –мост Уитстона предназначен для измерения величин сопротивлений. Он состоит из реохорда АВ, чувствительного гальванометра SHAPE \* MERGEFORMAT и двух резисторов – известной величины R и неизвестной – R _х. ( рис. 2).

Рис. 2

Реохорд представляет собой укрепленную на линейке однородную проволоку, вдоль которой может перемещаться скользящий контакт D. Рассмотрим схему без участка ЕD. Замкнем ключ К. Тогда по проволоке АВ потечет ток и вдоль нее будет наблюдаться равномерное падение потенциала от величины j _a (в точке А) до величины j _b (в точке В). В цепи АЕВ пойдет ток и будет наблюдаться падение потенциала от j _a до j _e (на резисторе R х) и от j _e до j _b (на резисторе R ). Очевидно, в точке Е потенциал имеет промежуточное значение j _e между значениями j _a и j _b . Поэтому на участке АВ всегда можно найти точку D, потенциал которой равен потенциалу в точке Е: j _D = j _e . Если между точками Е и D включен гальванометр, то в этом случае ток через него не пойдет, т.к. φ _e – φ _D = 0.

Такое состояние моста называется равновесием моста. Покажем, что условие равновесия определяется соотношением

. (1)

Действительно, на основании второго закона Кирхгофа для любого замкнутого контура алгебраическая сумма падений потенциала равна алгебраической сумме электродвижущих сил e :

. (2)

Запишем эти условия для контуров АЕ D и ЕВD в случае уравновешенного моста (рис. 2):

; (3)

. (4)

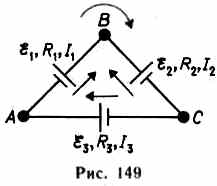
Используем первый закон Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: . Узлом называется точка или место соединения трех и более проводников (рис. 2). Для узла Е: I_X – I + I_G = 0. При равновесии моста I_G = 0, тогда получим , . Из (3) и (4) получим

, .

Деля первое на второе, найдем соотношение (1). Так как сопротивление изотропного проводника цилиндрической формы зависит от геометрических размеров и материала, т.е. , где – удельное сопротивление проводника; l , S – длина и площадь сечения проводника, то сопротивление участков реохорда АВ можно записать в виде

; . (5)

Подставляя (5) в (1), получим искомую рабочую формулу

, (6)

где и – длины плеч реохорда АВ; R – сопротивление, подбираемое магазином сопротивлений.

Мост Уитстона может быть также использован для определения внутреннего сопротивления гальванометра r , причем гальвано
метр SHAPE \* MERGEFORMAT в этом случае включается, как показано на рис. 3.

Рис. 3

Если потенциалы j _e и j _D равны, то сила тока в диагонали ЕD равна нулю, а поэтому замыкание и размыкание ключа К₁ не будут вызывать изменения силы тока в ветвях мостовой схемы, в том числе и в ветви гальванометра.

При равенстве потенциалов j _e и j для моста имеет силу формула

, (7)

по которой непосредственно определяется измеряемое сопротивление гальванометра. Таким образом, мостовая схема может быть использована для измерения сопротивлений не только в том случае, когда гальванометр включен в ее диагональ, но и тогда, когда он включен в одно из ее плеч. В этом случае надо при измерении добиваться постоянства показания гальванометра при замыкании и размыкании ключа в указанной диагонали схемы.

Такой прием применяется для измерения сопротивления гальванометра, т.к. он не требует включения второго прибора в диагональ схемы.

Ход работы

Упражнение 1. Измерение величины сопротивления двух проводников, а также общего сопротивления при их последовательном и параллельном соединениях.

1. Собрать схему, изображенную на рис. 2.

2. Измерить величину сопротивления R х₁, а также последующих сопротивлений (три раза). Для этого установить движок реохорда на середину ( ) и подбором величины сопротивления магазина R уравновесить мост, то есть добиться нулевого положения стрелки при включенном питании.

Повторить измерения при и , устанавливая движок реохорда вблизи его середины ( тем самым достигается минимальная погрешность результата). Измеряемая величина сопротивления определяется по формуле

.

3. Включить в цепь R_{x 2} вместо R_{x 1} и измерить его величину согласно п. 2.

4. Измерить величины сопротивлений последовательного и параллельного соединений R_{x 1} и R_{x 2} , включаемых вместо R_x в плечо АЕ (рис. 2). Измерения проводить согласно требованиям
пункта 2.

и

рассчитать значения величин сопротивлений и сравнить их со значениями, полученными при выполнении пункта 4.

6. Результат измерений занести в таблицу 1.

Источник

Правила Кирхгофа. Обобщенный закон Ома (см

Обобщенный закон Ома (см. (100.3)) по­зволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источни­ков э.д.с. и т. д.), довольно сложен. Эта задача решается более просто с помощью двух правил Кирхгофа.

Любая точка разветвления цепи, в ко­торой сходится не менее трех проводников с током, называется узлом.При этом ток, входящий в узел, считается положитель­ным, а ток, выходящий из узла,— отрица­тельным.

Первое правило Кирхгофа:алгебраи­ческая сумма токов, сходящихся в узле, равна нулю:

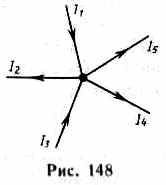
Например, для рис. 148 первое правило Кирхгофа запишется так:

Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке про­водника и ни на одном его участке не должны накапливаться электрические за­ряды. В противном случае токи не могли бы оставаться постоянными.

Второе правило Кирхгофа получается из обобщенного закона Ома для разветвлен­ных цепей. Рассмотрим контур, состоящий

из трех участков (рис. 149). Направление обхода по часовой стрелке примем за по­ложительное, отметив, что выбор этого на­правления совершенно произволен. Все токи, совпадающие по направлению с на­правлением обхода контура, считаются по­ложительными, не совпадающие с на­правлением обхода — отрицательными. Источники э.д.с. считаются положительны­ми, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:

Складывая почленно эти уравнения, по­лучим

Уравнение (101.1) выражает второе правило Кирхгофа:в любом замкнутом контуре, произвольно выбранном в развет­вленной электрической цепи, алгебраиче­ская сумма произведений сил токов I_i, на сопротивления R_i соответствующих участков этого контура равна алгебраиче­ской сумме э.д.с. ξ _k, встречающихся в этом контуре:

При расчете сложных цепей постоян­ного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действитель­ное направление токов определяется при решении задачи: если искомый ток полу­чится положительным, то его направление было выбрано правильно, отрицатель­ным — его истинное направление противо­положно выбранному.

2. Выбрать направление обхода кон­тура и строго его придерживаться; про­изведение IR положительно, если ток на данном участке совпадает с направлением обхода, и наоборот, э.д.с., действующие по выбранному направлению обхода, счита­ются положительными, против — отрица­тельными.

3. Составить столько уравнений, что­бы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рас­сматриваемой цепи); каждый рассматри­ваемый контур должен содержать хотя бы один элемент, не содержащийся в преды­дущих контурах, иначе получатся уравне­ния, являющиеся простой комбинацией уже составленных.

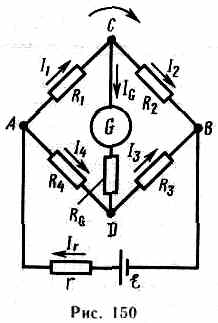
В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измери­тельного моста Уитстона.Сопротивления R₁, R₂, R₃и R₄ образуют его плечи. Между точками А и В моста включена батарея с э.д.с. ξ и со­противлением r, между точками С и D включен гальванометр с сопротивлением R_G. Для узлов А, В и С, применяя первое правило Кирхгофа, получим

Для контуров АСВξА, ACDA и CBDC, соглас­но второму правилу Кирхгофа, можно запи­сать:

Если известны все сопротивления и э.д.с., то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R₂, R₃и R₄, можно добиться того, чтобы ток через гальванометр был равен нулю (I_G=0). Тогда из (101.3) найдем

а из (101.4) получим

Таким образом, в случае равновесного моста (I_G=0) при определении искомого сопротивле­ния R₁э.д.с. батареи, сопротивления батареи и гальванометра роли не играют.

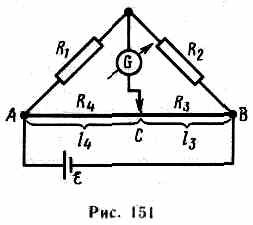
На практике обычно используется реохордный мост Уитстона(рис. 151), где сопротивле­ния R₃ и R₄ представляют собой длинную одно­родную проволоку (реохорд) с большим удель­ным сопротивлением, так что отношение R₃/R₄ можно заменить отношением l₃/l₄. Тогда, ис­пользуя выражение (101.7), можно записать

Длины l₃ и l₄ легко измеряются по шкале, a R₂всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное со­противление R₁.

Заключительная часть Ответы на вопросы. Подведение итогов

Источник